OMRÅDEFORMLER - TABEL OVER OMRÅDEFORMLER FOR FORSKELLIGE FORMER

Områdeformler for forskellige objekter er formlerne, der bruges til at finde arealet af forskellige objekter. Arealet er det rum, der optages af grænsen for enhver figur. Områdeformler for forskellige geometriske former er afhængige af forskellige parametre, såsom dimensioner, højde og radius af forskellige geometriske former. Geometriske former er af to typer, der er:

Todimensionelle former (2D-former)
Tredimensionelle former (3D-former)

I denne artikel vil vi lære om arealformler for forskellige 2-D og 3-D former, såsom areal af rektangel, areal af kvadrat, areal af cirkel, areal af terning osv. og andre i detaljer.

Indholdsfortegnelse

Hvad er areal?
Hvad er områdeformler?
Hvad er 2D-former?
Formel for 2D-former
Område formler tabel
Hvad er 3D-former?
Formel for 3D-former
Eksempler på områdeformler

Hvad er areal?

Den plads, der optages af grænsen for en figur, kaldes areal af figuren. Det måles i enhedskvadrat. SI-enheden til at måle arealet er m². Areal bruges i forskellige matematiske begreber og bruges også i scenarier i det virkelige liv, såsom at finde arealet af værelse, arealbord osv. og andet.

Hvad er områdeformler?

Områdeformler er væsentlige værktøjer, der bruges i matematik til at beregne mængden af rum, der er omsluttet af forskellige todimensionelle former. Disse formler kan bruges til at finde arealet af geometrisk figurer som firkanter, rektangler, cirkler, trekanter, trapezoider og ellipser. Ved at bruge disse formler kan vi nøjagtigt beregne arealet af forskellige former, hvilket gør os i stand til at løse problemer i den virkelige verden og foretage vigtige beregninger.

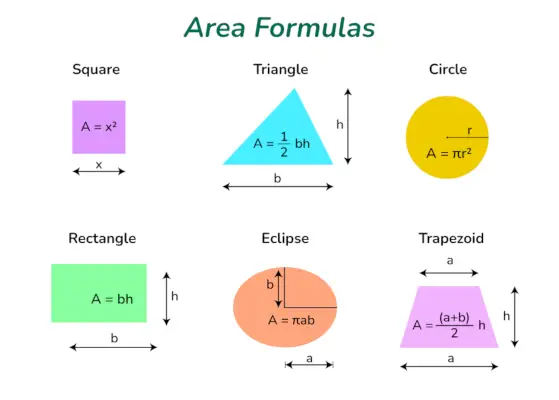
Områdeformler

Hvad er 2D-former?

Former, der kun har to dimensioner, kaldes 2-D former . De er tegnet i 2-D rum og er afhængige af 2 parametre, generelt længde(l) og bredde(b). De forskellige 2D-former er, Rektangel, Firkant, Trekant, Cirkler og andre.

Formel for 2D-former

Areal af 2D-former formler er den formel, der bruges til at kæle for arealet af de forskellige 2D-former, såsom areal af trekant, areal af kvadrat, areal af rektangel, areal af rombe osv. Disse arealformler er meget brugt i matematik til at løse forskellige geometriske problemer. Forskellige områdeformler for forskellige former er,

Arealformel for et rektangel

Rektangel er en 2-dimensionel figur som er en firkant, dvs. den har fire sider dens modstående sider er parallelle og lige store. Alle vinklerne i rektanglet er lige store, og deres mål er 90 grader. Diagonalerne i rektanglet er lige store, og de er vinkelrette halveringslinjer på hinanden.

Formlen til at beregne arealet af et rektangel er med længde og l og bredde b er,

Areal af rektangel (A) = l×b kvadratenheder

Områdeformel for en firkant

Kvadrat er en 2-dimensionel figur, som er en firkant, dvs. den har fire sider, dens modstående sider er parallelle, og alle fire sider i en firkant er lige store. Alle vinklerne i kvadratet er lige store, og deres mål er 90 grader. Kvadratens diagonaler er lige store, og de er vinkelrette halveringslinjer på hinanden.

Formlen til at beregne arealet af et kvadrat med side -en er,

Areal af kvadrat (A) = a ² kvm enheder

Arealformel for en trekant

Trekant er den enkleste polygon, som er lavet ved at forbinde tre rette linjer. Som navnet antyder er det en polygon med tre vinkler. Summen af længderne af alle sider af trekanten er trekantens omkreds, og rummet inde i trekantens omkreds er trekantens areal.

afgrænser java

Formlen til beregning af arealet af en trekant med base b er og højde h er,

Areal af trekant (A) = 1/2 × bh kvadratenheder

Områdeformel for en cirkel

Cirkel er en geometrisk figur uden lige linje. Det er stedet for punktet, der altid er i konstant afstand fra det faste punkt. Det faste punkt kaldes cirklens centrum og den faste afstand er cirklens radius.

Formlen til beregning af areal af en cirkel med r som radius af cirklen er,

Cirkelareal (A) = πr ² kvm enheder

Områdeformel for et parallelogram

Parallelogram er en 2-D figur hvor de modsatte sider er parallelle og lige store. Formlen til beregning af arealet af parallelogram med base b og højde h er,

Areal af parallellogram (A) = bh kvadratenheder

Områdeformel for en Rhombus

Rhombus er en firkant med alle fire sider lige store og parallelle, men ikke alle vinkler er lige store. Formlen til beregning af arealet af rombe med diagonal d ₁ og d ₂ er,

Areal af Rhombus (A) = 1/2 × d ₁ × d ₂ kvm enheder

Områdeformel for en trapez

Trapez er et andet navn på trapez . Det er en firkant, hvor de modsatte sider er parallelle. Formlen til beregning af arealet af trapez med parallelle sider -en og b og højde h er,

Areal af trapez (A) = 1/2(a +b)h kvadratenheder

Områdeformel for en Ellipse

Ellipse er en 2-D form og kommer under koniske sektioner. Formlen til beregning af arealet af en ellipse med akse som -en og b er,

Areal af Ellipse (A) = πab kvadratenheder

Områdeformel for en halvcirkel

Halvcirkel er en 2-D figur, som er halvdelen af cirklen. Formlen til at beregne arealet af halvcirkel med radius r er,

Areal af halvcirkel (A) = 1/4(πr ² ) kvm enheder

Område formler tabel

Formlerne for områderne af de forskellige 2-D figurer er tilføjet i tabellen tilføjet nedenfor,

Figurer	Formel	Variabler
Rektangel	Areal = l×b	l er længden b er bredden
Firkant	Areal = a²	a er siden af firkanten
Trekant	Areal = 1/2×bh	b er basen h er højden
Cirkel	Areal = πr²	r er radius af cirklen
Trapez	Areal = 1/2×(a+b)h	a er den første base b er den anden base
Rhombus	Areal = 1/2×d₁×d₂ python os listedir	d₁er den ene diagonal d₂er den anden diagonal
Parallelogram	Areal = b × h	b er basen h er højden
Ellipse	Areal = πab	a er radius af hovedaksen b er radius af lille akse

Hvad er 3D-former?

3-D-former er de figurer, der er tegnet i 3-D-rum. De har 3 dimensioner, der er deres parametre. Arealet af disse figurer afhænger af længden, bredden og højden af 3-D figurer. Forskellige 3D-former er, Cube, Cuboid, Cylinder, Cone, Sphere og andre. Areal af 3-D-former er af to kategorier, der er buet overfladeareal (lateral overfladeareal){CSA} og totalt overfladeareal (TSA). CSA er arealet af al den buede overflade af 3-D-formerne, og TSA er arealet af alle 3-D-formernes flader.

Formel for 3D-former

Arealet af 3-D-formerne er den plads, der optages af alle figurens ansigter. Det måles i enhed². SI-enheden for arealet er m². Det terningens område , område af cuboid , område af cylinder, område af kegle og andre kommer i området for 3D-former. Tabellen tilføjet nedenfor viser formlerne for forskellige 3D-figurer.

Område af form	Overfladeareal	Parametre
Område af Cube	6a²	a er kantens længde
Område af Cuboid	2(lb + lh + bh)	l er kantens længde b er bredden af kanten h er Kanthøjden
Kegleområde	πr(r + l)	r = radius af cirkulær base l = skrå højde
Område af cylinder	2π(r + h)	r = radius af cirkulær base h = højden af cylinderen
Område af sfære	4πr²	r er kuglens radius
Område af halvkugle	3πr²	r er radius af halvkugle
Areal af rektangulært prisme	2(wl + hl + hw)	l er kantens længde w er kantens bredde h er Kanthøjden

Tjek også

Areal- og perimeterformler

Formler for overfladeareal

Eksempler på områdeformler

Eksempel 1: Find arealet af et rektangel med en længde på 5 cm og en bredde på 2 cm.

Løsning:

givet,

Længde af rektanglet (l) = 5 cm

Bredde af rektanglet (b) = 2 cm

Arealet af rektangel(A) = l × b

A = 5 cm × 2 cm
= 10 cm²

Eksempel 2: Find arealet af firkantparken, hvis side er 4 m.

Løsning:

givet,

Side af kvadratet (a) = 4 m

Areal af kvadrat = a²
= (4)²= 16 m²

Pladsparkens areal er således 16 m²

Eksempel 3: Find arealet af en trekantet plade, hvis højde er 6 cm og bunden er 6 cm.

Løsning:

givet,

Trekantens højde (h) = 6 cm

Basen af trekanten (b) = 8 cm

Areal af trekant(A) = 1/2(b × h)

A = 1/2(8 × 6)
= 48/2 = 24 cm²

Arealet af den trekantede plade er 24 cm²

Eksempel 4: Find arealet af en cirkulær skive med en radius på 1,4 cm.

Løsning:

givet,

Cirkelradius (r) = 1,4 cm

Arealet af cirkel(A) = πr²

A = π(1,4)²
= 22/7(1,4)(1,4) = (4,4)(1,4)
= 6,16 cm²
java server sider

Arealet af den cirkulære skive er 6,16 cm²

Ofte stillede spørgsmål om områdeformler

Hvad er områdeformler?

Arealformlerne er de formler, der bruges til at finde arealet af enhver figur. Det bruges til at finde mængden af plads optaget af figuren. Generelt er området repræsenteret med bogstavet 'A'. og måles i enhed², dvs. cm², m², etc.

Hvad er Area Formula For Square?

Arealformlen for et kvadrat er formlen til at beregne pladsen optaget af kvadratet. Formlen til at beregne arealet af kvadratet er,

Areal af kvadrat = (side) ²

Hvad er arealformel for rektangel?

Arealformlen for et rektangel er formlen til at beregne pladsen optaget af rektanglet. Formlen til at beregne arealet af rektanglet er,

Areal af rektangel = Længde × Bredde

Hvad er arealformel for trekant?

Arealformlen for en trekant er formlen til at beregne pladsen optaget af trekanten. Formlen til at beregne arealet af trekanten er,

Trekantareal = 1/2 (grundlag × højde)

Hvad er områdeformel for cirkel?

Arealformlen for en cirkel er formlen til at beregne den plads, cirklen optager. Formlen til at beregne arealet af cirklen er,

Cirkelareal = π(radius) ²

Hvad er områdeformel for firkantet?

Formel til at beregne arealet af firkantet,

Areal af firkantet = 1/2 × diagonal ₁ × Diagonal ₂

Hvad er arealformlen for trekantet prisme?

Formel for arealet af trekantet prisme er,

Areal af trekantet prisme = (omkreds af base × længde af prisme) + 2 × basisareal

Hvad er arealformel for polygon?

Formlen til at beregne arealet af polygon er,

Polygonareal = 1/2 × (perimeter × apotem)

Hvad er arealformlen for retvinklet trekant?

Formel for arealet af retvinklet trekant er,

Areal af retvinklet trekant = 1/2 × vinkelret × base

Hvad er Area Formula of Pentagon?

Formlen for området Pentagon er,

Areal af Pentagon = 1/2 × Perimeter × Apotem