Trapezium i matematik: Et trapez er en polygon med fire sider, dvs. det er en firkant. Trapezium stammer fra det græske ord trapez, som betyder bord. Det er en kompleks firkant. Et trapez er en speciel firkant med kun et par parallelle sider. Et trapez er en todimensionel form, der fremstår som en tabel.
Et trapez har fire sider og fire hjørner. Vi ser trapezformen i vores daglige liv, og det er en af de mest almindelige former. I denne artikel vil vi lære om hvad er trapez i matematik, dets egenskaber, formler, eksempler og typer af trapez, sammen med nogle løste eksempler på det.
Indholdsfortegnelse
- Hvad er et trapez i matematik?
- Typer af trapez
- Uregelmæssigt trapez
- Trapeziums egenskaber
- Trapezium formel
- Område med trapezformel
- Omkreds af trapezformel
- Forskellen mellem trapez og trapez
- Trapeziums vinkler
- Diagonal af trapez
- Trapezium eksempler
Hvad er et trapez i matematik?
Et trapez er en lukket todimensionel firkant med et par parallelle modstående sider. De parallelle sider af et trapez kaldes baser, og de ikke-parallelle sider af et trapez kaldes ben. Trapezium har fire sider og fire hjørner. EN parallelogram kaldes også et trapez med to parallelle sider.
Trapezium definition
Et trapez er en firkant (en firesidet polygon) med mindst et par parallelle sider. Disse parallelle sider kaldes trapezets baser, og de to andre sider kaldes benene, som ikke nødvendigvis er parallelle.
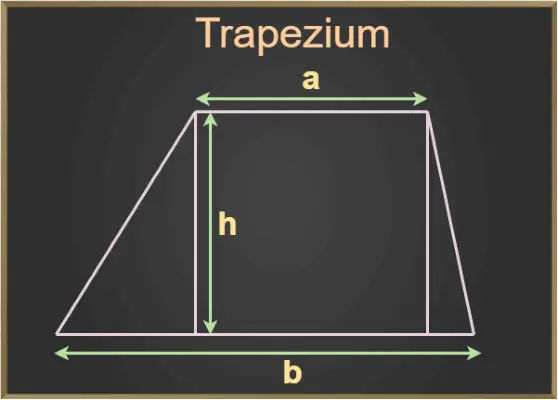
I ovenstående figur er a og b baserne for trapezet, og h er højden af trapezet.
Trapezium form
Trapezium er en firkantet dvs. polygon med fire sider. Et trapez har fire sider med et par modstående sider parallelt med hinanden. Trapeziumformen er meget almindelig, og vi ser forskellige ting i vores dagligdag, der ligner trapez. Nogle af de virkelige eksempler på trapez, som vi observerer, er trapezformede borde, fliser, malerier og andre.
Typer af trapez
Baseret på siderne og vinklerne er trapez af tre typer:
- Scaleen Trapezium
- Ligebenet trapezium
- Højre trapezium

Ligebenet trapezium
Trapeziet, som har lige lange ben, kaldes et ligebenet trapez, dvs. i et ligebenet trapez er de to ikke-parallelle sider lige store.
Scaleen Trapezium
Et trapez, hvor alle siderne ikke er ens, kaldes et scalene trapez. I et skalentrapez er ikke to vinkler ens.
Højre trapez
Et trapez, der har et retvinklet par, støder op til hinanden, er kendt som et ret trapez.
Uregelmæssigt trapez
Et trapez har et par parallelle sider, og de to andre sider er ikke-parallelle. I et regulært trapez er de to andre ikke-parallelle sider lige store, men i tilfælde af et uregelmæssigt trapez er de to ikke-parallelle modstående sider uens.
Trapeziums egenskaber
Der er forskellige egenskaber ved trapez, hvoraf nogle er som følger:
- Parallelle sider: Et trapez har to parallelle sider, som kaldes baser. Eksempel: Siderne AB og CD er parallelle med hinanden, vist på figuren.
- Ikke-parallelle sider: Ikke-parallelle sider af et trapez kaldes benene, og benene på et trapez er ikke lige lange. Eksempel: Sider AD og BC er ikke-parallelle sider af trapez.
- Højde eller højde: Vinkelret afstand mellem baserne kaldes højden eller højden af trapez. I ovenstående diagram er h højden af trapezium.
- Summen af vinkler
- Tilstødende indvendige vinkler i et trapez summer op til 180°. Eksempel: Der er to par co-indvendige vinkler. Det ene par er ∠ A og ∠ D, mens det andet par er ∠ B og ∠ C. Summen af hvert par af co-indvendige vinkler er 180°.
- Summen af alle indvendige vinkler i et trapez er altid 360°. Eksempel : På figuren er ∠A+∠D 180° og ∠B+∠C er 180°. Derfor ∠A+∠D +∠B+∠C = 360°.
- Median: Medianen af et trapez er det linjestykke, der forbinder benens midtpunkter. Medianen er parallel med baserne, og dens længde er gennemsnittet af længderne af baserne.
- Trapezium har præcis ét par modsatte sider, der er parallelle.
Trapezium formel
Vigtige formler for et trapez er:
- Trapeziumområde = ½ (Sum af parallelle sider) × (Afstand mellem parallelle sider)
- Omkreds af trapez = Summen af alle fire sider
Område med trapezformel
Trapezium har to parallelle sider henholdsvis a og b enheder, og dets højde er h.
Nu kan arealet af trapez beregnes ved at finde gennemsnittet af baser og gange dets resultat med højden. Derfor,
npm cache ren
Trapeziumområde = ((a +b)/2) × h
hvor,
- -en og b er baser af trapez
- h er Højde
Område med ligebenet trapez
Lad a og b være længden af parallelle sider af et trapez ABCD, hvor a og b er basene af trapez og a>b.
Nu, da det er et ligebenet trapez, er c længden af begge de to ikke-parallelle sider, og h er højden af trapez.
Nu er AB = a, CD = b, BC = AD = c
I retvinklet trekant , AED
Længde af vinkelret, h = √(c 2 – (a-b) 2 ) [ved brug af Pythagoras sætning ]….(1)
Nu,
Areal = ½ × summen af parallelle sider × højden af trapez
Areal = ½ × (a+b) × h
Brug af ligning (1)
Område med ligebenet trapez = 1/2 × [√(c 2 – (a-b) 2 ) (a+b)]
Omkreds af trapezformel
Omkredsen af et trapez er givet ved at beregne summen af alle dets sider. Derfor,
Omkreds af trapez = AB + BC + CD + AD
hvor, AB, BC, CD og AD er sider af trapez
Omkreds af ligebenet trapez
Hvis i et ligebenet trapezium a og b er længderne af parallelle sider, dvs. baserne, og c er længden af to lige store ikke-parallelle sider, så er omkredsen givet ved:
Omkreds = a + b + 2c
hvor,
- -en , b er baser af trapez
- c er Lige Side af Trapezium
Forskellen mellem trapez og trapez
Generelt er både Trapezium og Trapezoid de samme, men forskellen ligger i deres oprindelsesland.
- Trapezium er af britisk oprindelse, det er en firesidet polygon og en todimensionel figur har den nøjagtigt et par parallelle sider modsat hinanden. I Indien følger vi britisk engelsk, derfor bruges ordet Trapezium.
- Trapez er af amerikansk oprindelse, det er også en firesidet polygon med et par parallelle sider modsat hinanden. Parallelle sider er baserne og yderligere to ikke-parallelle sider kaldes trapezets ben.
Trapeziums vinkler
Trapezium er en firkant, og summen af alle vinklerne i en firkant er 360 grader. Så summen af alle trapezets indre vinkler er 360 grader.
For ethvert regulært trapez, dvs. det trapez, hvor ikke-parallelle sider er lig med de tilstødende vinkler, der dannes mellem den parallelle linje og den ikke-parallelle linje, er ens. Summen af disse to vinkler er således supplerende.
Lad os tage et eksempel for at understøtte dette koncept for et ligebenet trapez ABCD, hvis AB er parallel med CD og AD er lig med CD, så ved vi, at ∠A = ∠B og ∠C = ∠D så,
∠A + ∠B + ∠C + ∠D = 360°
Her er ∠A = ∠B og ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Tilsvarende er (∠B + ∠D) = 180°
Diagonal af trapez
Trapezium er en speciel type firkantet; således har trapez også to diagonaler. Diagonalerne af et trapez har ikke samme længde, i modsætning til i nogle andre firkanter såsom rektangler eller parallelogrammer. Diagonaler af trapez har ikke lige store længder, og længderne af diagonalerne afhænger af længderne af baserne og vinklerne på trapez.
Eksempel: For et ligebenet trapez ABCD er grundvinklen ∠A 80° og find derefter den anden vinkel ∠C.
Vi ved, at for en ligebenet trapezium ABCD,
(∠A + ∠C) = 180°
aftensmad vs middagstidGivet, ∠A = 80°
Nu, 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
Påkrævet vinkel ∠C er således 100°
Trapeziumformler – Areal og omkreds af trapez
Formler relateret til trapez er opsummeret i følgende tabel:
import myre
| Ejendom | Formel |
|---|---|
| Areal | 1/2 × ( -en + b ) × h |
| Område (ligebenet trapezium) | 1/2 × [√(c2– (a-b)2) (a+b)] |
| Omkreds | -en + b + c + d |
| Omkreds (ligebenet trapezium) | -en + b + 2 c |
| Median | (en + b)/2 , |
Folk læser også:
- Rhombus
- Trekant
- Hvad er formel for at finde et område med trapez?
Trapezium eksempler
Eksempel 1: Find den fjerde side af trapezet, hvis de tre andre sider er 8 cm, 12 cm og 16 cm, og omkredsen er 40 cm.
Løsning:
Omkreds er givet som summen af alle dens sider. Lad længden o ukendt være 'x'-enheder.
Omkreds = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Således er længden af den ukendte side 4 cm
Eksempel 2: Et trapez har parallelle sider med længderne 15 cm og 11 cm og ikke-parallelle sider med en længde på hver 5 cm. Beregn omkredsen af trapez.
Løsning:
Det er et ligebenet trapez, fordi det tydeligt nævnes, at ikke-parallelle sider med en længde på 5 cm hver er lige store.
Ifølge Isosceles Trapezium, hvis to ikke-parallelle sider af Trapezium er lige lange, er det kendt som Isosceles Trapezium.
givet,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Omkreds = a + b + 2c
P = 15 + 11 + 2(5)
P = 15 + 11 + 10
P = 36 cm
Eksempel 3: Find omkredsen af et trapez, hvis sider er 12 cm, 14 cm, 16 cm og 18 cm.
Løsning:
P = Summen af alle sider
P = 12 + 14 + 16 + 18
P = 60 cm
Derfor er omkredsen af trapez 60 cm
Eksempel 4: Find arealet af trapez, hvor summen af parallelle sider er 60 cm, og dets højde er 10 cm.
Løsning:
givet,
- Sum af parallelle sider 60 cm
- højde, h = 10 cm
Areal af trapez, A = 1/2 × Summen af parallelle sider × Afstand mellem parallelle sider
int til strengErstatning af givne værdier,
A =1/2×60×10
A = 30×10
A = 300 cm2
Derfor er areal af trapez =300 cm2
Øv opgaver på trapezium i matematik
1. Find arealet af et trapez med baser på 10 cm og 15 cm og en højde på 6 cm.
2. Et trapez har et areal på 54 kvadratmeter. Hvis en af baserne er 12 meter lang og højden er 6 meter, så find længden af den anden base.
3. Beregn omkredsen af et trapez med baser på 8 cm og 14 cm og ikke-parallelle sider på 5 cm og 7 cm.
4. Bestem længden af midtersegmentet i et trapez, hvor bunden måler 18 cm og 30 cm.
5. I et ligebenet trapez er vinklerne ved den ene base hver 45 grader. Find målene for vinklerne ved den anden base. Antag, at trapezet ikke er et højre trapez.
Resumé – Trapezium i matematik
Et trapez er en firesidet polygon eller firkant, kendetegnet ved at have et par parallelle sider kaldet baser, mens de to andre sider, kendt som ben, ikke er parallelle. Trapezium er almindeligt i hverdagsgenstande som tabeller og er bemærkelsesværdigt for dets geometriske egenskaber: det har en højde, som er den vinkelrette afstand mellem baserne, og en median, der forbinder midtpunkterne på de ikke-parallelle sider og er parallel med baserne.
Arealet af et trapez beregnes ved at tage et gennemsnit af længderne af baserne og gange med højden, mens dets omkreds er summen af alle dets sider. Med forskellige klassifikationer såsom skala, ligebenet og højre trapez, hver med unikke side- og vinkelegenskaber, er trapez grundlæggende i både praktiske anvendelser og geometrisk teori.
Ofte stillede spørgsmål om Trapezium i matematik
Hvad er trapezform?
Trapezium er en firkant, hvor et par linjer altid er parallelle. Det ligner formen på et bord. Dens navn er taget fra det græske ord trapez, som betyder bord.
Hvor mange typer trapez?
Der er to typer trapez,
- Almindelig trapez: Hvor det andet par linjer er lige store.
- Uregelmæssigt trapez: Hvor det andet linjepar ikke er ens.
Hvor mange parallelle sider har et trapez?
Vi ved, at trapez er en firkant med et par parallelle sider. Således har et trapez et par parallelle linjer(sider).
Kan et trapez betragtes som en firkant?
A har fire sider, fire hjørner og fire vinkler. Derfor kan det betragtes som en firkant, summen af alle fire indre vinkler af et trapez er 360 grader.
Kan en firkant kaldes et trapez?
Et trapez er en firkant med kun et par parallelle sider, og de to andre sider er ikke-parallelle. Men i tilfælde af en firkant har den to par parallelle sider, derfor kan den ikke betragtes som et trapez.
Er diagonaler af et trapez altid lige store?
Diagonaler af et trapez er muligvis ikke ens. I tilfælde af en regulær polygon er diagonalerne ens, men dette er ikke sandt i tilfælde af en uregelmæssig polygon.
Hvad er egenskaberne ved et trapez?
5 egenskaber ved et trapez er:
- I trapez er baser parallelle med hinanden.
- Et trapez har supplerende tilstødende vinkler.
- Kun ét par modstående sider er parallelle.
- Summen af alle indvendige vinkler i et trapez er altid 360°.
- Linje, der forbinder midtpunktet af ikke-parallelle sider, er altid parallel med baser.
