EN Fungere i matematik er en særlig relation mellem sættet af inputværdier og sættet af outputværdier. I Funktion giver hver inputværdi en bestemt outputværdi. Vi repræsenterer en funktion i matematik som, y = f(x) hvor x er inputværdien og for hver x vi får en outputværdi som y.

I denne artikel vil vi lære om, funktioner i matematik, deres forskellige typer, eksempler og andre i detaljer.

Indholdsfortegnelse

• Hvad er en funktion i matematik?
• Funktionsdefinition i matematik
• Eksempler på funktioner
• Betingelse for en funktion
• Repræsentation af funktioner i matematik
• Identifikation af funktion
• Typer af funktioner
• Hvad er en funktion i algebra?
• Domæne og rækkevidde af en funktion
• Sammensætning af funktioner
• Algebra af funktioner
• Hvad er en funktion på en graf?
• Grafiske funktioner
• Fælles funktioner
• Anvendelser af funktioner
• Eksempler på funktion
• Øv problemer om, hvad der er en funktion

Hvad er en funktion i matematik?

En funktion i matematik er en forhold mellem inputværdierne (domæne) og outputværdierne (range) for de givne sæt, således at ikke to variable fra domænesættene er knyttet til den samme variabel i intervalsættet. Et simpelt eksempel på en funktion i matematik er f(x) = 2x, som er defineret på R→R, her er enhver variabel i domænet relateret til kun én variabel i området.

En funktion i matematik har et domæne, codomæne og rækkevidde. Domænet er mængden af ​​alle mulige værdier af x, og rækkevidden af ​​funktionen er mængden af ​​alle outputværdier af y. Området er delmængden af ​​codomæne for en funktion. Vi kan også sige, at en funktion i matematik er en relation med et unikt output, og ingen to inputværdier har lignende output i en funktion, hvilket er tilfældet for relation.

Funktionsdefinition i matematik

Funktion er en speciel relation eller metode, der forbinder hvert medlem af sæt A til et unikt medlem af sæt B via en defineret relation. Sæt A kaldes domænet og sæt B kaldes funktionens co-domæne. En funktion i matematik fra mængde A til mængde B er defineret som,

f = ∀ a ∈ A, b ∈ B

Enhver funktion er en relation, men enhver relation er ikke en funktion. Kriterierne for, at enhver relation kan betragtes som en funktion, da hvert element i mængde A kun har ét billede i sæt B, mens et element i sæt A i relation kan have mere end ét billede i sæt B.

Vi definerer en funktion i matematik fra ikke-tomt sæt A til ikke-tomt sæt B, således at,

(a, b) ∈ f, så f(a) = b

hvor vi ringede b som billede af -en defineret under relationen f .

Hvert element 'en' af sæt A har et unikt billede ' b ’ i sæt B så er det en funktion.

Eksempler på funktioner

En funktion i matematik f er defineret som, y = f(x) hvor x er inputværdien, og for hver inputværdi af x får vi en unik værdi af y. Forskellige eksempler på funktionerne i matematik defineret på R→R er,

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 osv

Betingelse for en funktion

For to ikke-tomme sæt A og B, en funktion f: A→B betegner det f er en funktion fra A til B, hvor EN er et domæne og B er et co-domæne.

For ethvert element, a ∈ A, et unikt element, b ∈ B er der sådan, at (a,b) ∈ f. Det unikke element b, som er relateret til a, er betegnet med f(a) og læses som f af a. Dette kan bedre forstås fra billedet nedenfor:

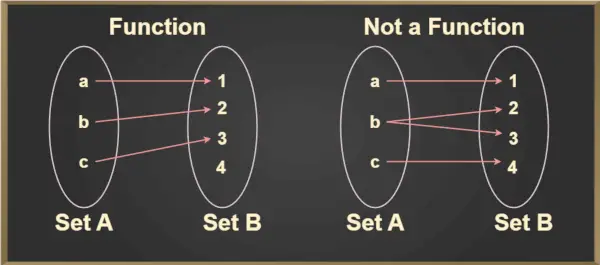
Vertikal linjetest

Vertikal linjetest bruges til at bestemme, om en kurve er en funktion eller ej. Hvis en kurve skærer en lodret linje ved mere end et punkt, er kurven ikke en funktion.

Repræsentation af funktioner i matematik

Vi repræsenterer en funktion i matematik som,

y = f(x) = x + 3

Her er værdisættet af x funktionens domæne, og sættet af outputværdier af y er funktionens co-domæne. Her er funktionen defineret for alle reelle tal, da den giver en unik værdi for hvert x, men det er ikke altid muligt at få output for hver værdi af x, hvis vi definerer funktionen i to dele, dette kan forstås som

• f(x) = 1/(x – 2), hvor x ≠ 2
• f(x) = x²hvor x ∈ {R}

Vi kan definere en funktion i matematik som en maskine, der tager noget input og giver et unikt output. Funktionen f(x) = x²defineres nedenfor som,

Vi kan repræsentere en funktion i matematik ved de tre metoder som,

• Sæt af bestilte par
• Tabel Form
• Grafisk Form

For eksempel, hvis vi repræsenterer en funktion som, f(x) = x³

En anden måde at repræsentere den samme funktion på er som sæt af bestilte par som,

f = {(1,1), (2,8), (3,27)}

I ovennævnte sæt er funktionens domæne D = {1, 2, 3} og rækkevidden af ​​funktionen er R = {1, 8, 27}

Identifikation af funktion

Funktion klassificeres som en særlig type relation i matematik. Der er følgende regler, som kan bruges til at identificere en funktion:

• En relation, hvor hvert input, der er afbildet til et unikt output, er en funktion. Dette kaldes en til en funktion.
• En relation, hvor to input(preimage) mappet til et enkelt output, er også en funktion. Dette er mange til én funktion.
• En relation, hvor et input er afbildet to forskellige output, er ikke en funktion.
• En relation, hvor mange input er afbildet til mange output efter ingen specifik regel, er ikke en funktion.

Typer af funktion

Forskellige Typer af funktioner bruges til at løse forskellige typer matematiske problemer især relateret til kurver og ligninger. Der er tre hovedtyper af funktioner i matematik, der er baseret på elementkortlægningen fra mængde A til mængde B.

Injektiv funktion eller en til en funktion

Funktionen, hvor hvert element i domænet har et særskilt billede i codomænet, kaldes Injektiv eller En-til-en funktion .

f: A → B siges at være en-til-en eller injektiv, hvis billederne af distinkte elementer i A under f er distinkte, dvs.

f(a ₁ ) = b ₁ , f(a ₂ ) = b ₂

hvor en₁, a₂∈ A og b₁, b₂∈ B

Surjektive funktioner eller Onto Function

Surjective Function er den funktion, hvor hvert element i codomænet har et præ-billede i domænet. Det kaldes også Til funktion hvilket betyder, at hvert element af codomæne er forbundet med hvert element i domænet. Intet element i codomæne bør have en tom relation. Antallet af elementer i codomæne og rækkevidde er det samme.

f: A → B siges at være på, hvis hvert element i B er billedet af et element af A under f, dvs. for hver b ϵ B, eksisterer der et element 'a' i A, således at f(a) = b.

Bijektiv funktion

Hvis en funktion har egenskaber af både Injective(Onto-En) og Surjective(Onto-funktion), så kaldes funktionen en Bijektiv funktion . I Bijective Function er hvert element i domænet relateret til hvert element i codomænet, og der er også en-til-en-relation. Dette indebærer, at antallet af elementer i codomænet og området er det samme, og at intet element hverken i domænet eller codomænet har tom relation.

Baseret på outputværdierne klassificeres funktionerne som ulige og lige funktioner. Lad os tage et kig på dem

Ulige funktioner

Ulige funktion er en type funktion, der udviser symmetri om oprindelsen. Specifikt, hvis f(x) er en ulige funktion, viser den, at f(-x) = -f(x)

Jævn funktion

Jævn funktion er en type funktion, der udviser symmetri om y-aksen. Specifikt, hvis f(x) er en lige funktion, viser den, at f(-x) = f(x)

Hvad er en funktion i algebra?

En funktion i algebra er en ligning, for hvilken ethvert x, der kan sættes ind i ligningen, vil producere nøjagtigt ét output, såsom y ud af ligningen. Det er repræsenteret som y = f(x), hvor x er en uafhængig variabel og y er en afhængig variabel.

For eksempel:

skrifttype gimp

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Domæne og rækkevidde af en funktion

Domæne og rækkevidde af en funktion er henholdsvis input- og outputværdi af en funktion. Lad os for eksempel sige, at vi har en funktion givet som f(x) = x². Her kan vi tage alt det reelle tal som inputværdien af ​​x, og outputtet vil altid være et positivt reelt tal. Derfor er dets domæne sat af alle reelle tal repræsenteret som R, mens dets område er sæt af positive reelle tal repræsenteret som R⁺

Sammensætning af funktioner

Hvis f: A → B og g: B→ C er to funktioner. Så er sammensætningen af ​​f og g betegnet som f(g), og den defineres som funktionen tåge = f(g(x)) for x ∈ A.

Lad os tage to funktioner f(x) = x + 3 og g(x) = 2x²

tåge = f(g(x))

⇒ tåge = f(2x²)

⇒ tand = 2x²+ 3

Lær mere, Sammensætning af funktion

Algebra af funktioner

Algebra af funktioner involverer de algebraiske operationer, der udføres mellem to funktioner. Den algebraiske operation for to funktioner f(x) og g(x) defineret på den reelle værdi af x er nævnt nedenfor:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (kf(x)) = k(f(x)); {For, k er et reelt tal}
• (f/g)(x) = f(x)/g(x); {For g(x) ≠ 0}

Hvad er en funktion på en graf?

En funktion kan let repræsenteres på en graf. Enhver funktion på grafen repræsenterer en kurve (inklusive en ret linje) i x-y-planet, der er kortlagt for dets input og tilsvarende outputværdier.

For at plotte en funktion på en skal du først finde nogle punkter, der ligger på funktionen, og derefter forbinde disse punkter i henhold til funktionens locus. For for eksempel at tegne funktionen (lige linie) f(x) = y = 5x – 2 skal vi bruge et punkt på grafen. For at finde punktet punktet på grafen tager vi først de tilfældige værdier af x og finder derefter deres tilsvarende værdier af y, som,

f(x) = y = 5x- 2

hvis x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

hvis x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

hvis x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Når vi nu forbinder disse punkter, kan vi få grafen for funktionen y = 5x – 2

Grafiske funktioner

At kende værdierne af x tillader en funktion f(x) at blive repræsenteret på en graf. Fordi y = f(x), kan vi finde den tilhørende værdi for y ved at starte med værdierne af x. Som et resultat kan vi plotte en graf i et koordinatplan ved hjælp af x- og y-værdier. Overvej følgende scenarie:

Antag y = x + 3

Når x = 0, er y = 3

Tilsvarende

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Som et resultat kan vi plotte grafen for funktion x + 3 ved at bruge disse værdier.

Fælles funktioner

Nogle almindelige funktioner, der almindeligvis bruges i matematik, er diskuteret nedenfor:

Virkelig funktion

Virkelig funktion i matematik refererer til en funktion, hvis domæne og område er delmængder af de reelle tal (betegnet som ℝ). I enklere vendinger er en reel funktion en matematisk regel eller et forhold, der tildeler en reel talværdi til hvert reelt tal input.

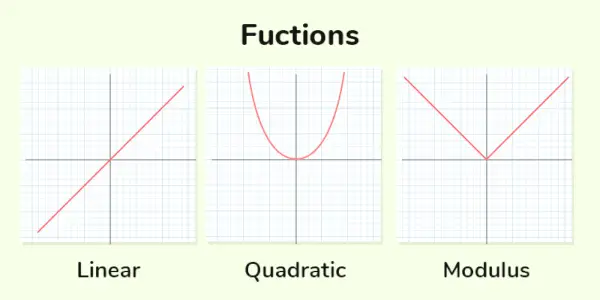
Virkelige funktioner

Polynomisk funktion

Funktionen, hvor eksponenterne af algebraiske variabler er ikke-negative heltal, kaldes a Polynomisk funktion . Hvis potensen af ​​variablen er 1 kaldes den en lineær funktion, hvis potensen er 2 kaldes den en andengradsfunktion, og hvis potensen er 3 kaldes den en kubisk funktion. Nogle eksempler på polynomiske funktioner er nævnt nedenfor:

• y = x²
• y = 2x + 3
• y = 3x³

Polynomisk funktion kan yderligere klassificeres i følgende typer:

Lineær funktion : Lineær funktion er dem, hvor den maksimale potens af variabel er 1. Den generelle form for Lineær funktion er y = mx + c

Kvadratisk funktion : Kvadratisk funktion er dem, hvor den maksimale effekt af variabel er 2. Generel form for kvadratisk funktion er, økse ² + bx + c = 0

Kubisk funktion : Kubisk funktion er dem, hvor den maksimale potens af variabel er 3. Generelt Form for kubisk funktion er givet som økse ³ + bx ² + cx + d = 0

Omvendt funktion

Omvendt funktion er den funktion, der indeholder det omvendte af en anden funktion. Lad os sige, at vi har en funktion y = f(x), så vil dens inverse funktion være x = f^-1(y). I y = f(x) er domænet x, og området er y, mens i tilfælde af x = f^-1(y), domænet er y og området er x. Således kan vi sige, at domænet for den oprindelige funktion er området for dens omvendte funktion, og området for den oprindelige funktion er domænet for den oprindelige funktion. Nogle eksempler på inverse funktioner er,

• y = så^-1(x)
• y = x^-1

Område funktion

Arealfunktion refererer typisk til en matematisk funktion, der beregner arealet af en geometrisk form eller et område. Arealfunktionen tager en eller flere parametre som input og returnerer arealet af den tilsvarende form. Nogle af områdefunktionerne diskuteres nedenfor:

Område med cirkelfunktion : Cirkelareal (A) er en funktion af dens radius(r), således at

A = πr ²

Område med trekantfunktion : Trekantområdet (A) er en funktion af dens base(b) og højde(h), således at,

A = (bh)/2

Eksponentiel funktion

Eksponentiel funktion er den, der er repræsenteret som f(x) = e^x. Det bruges ofte til at vise hurtig vækst eller forfald.

Logaritmisk funktion

Logaritmisk funktion er en matematisk funktion, der repræsenterer den inverse operation af eksponentiering. Det er repræsenteret som f(x) = log x.

Loft funktion

Loft funktion , angivet som ⌈x⌉, afrunder et reelt tal x op til det nærmeste heltal, der er større end eller lig med x. Med andre ord finder den den mindste heltalsværdi, der er større end eller lig med x.

Gulv funktion

Etagefunktion, angivet som ⌊x⌋, runder et reelt tal x ned til det nærmeste heltal, der er mindre end eller lig med x. Med andre ord finder den den største heltalsværdi, der er mindre end eller lig med x.

Modulus funktion

Modulus funktion , også kendt som den absolutte værdifunktion, returnerer størrelsen eller størrelsen af ​​et reelt tal uden hensyn til dets fortegn. Modulusfunktionen betegnes som ∣x∣, hvor x er inputværdien.

Signum funktion

Signum funktion , også kendt som fortegnsfunktionen eller signumfunktionen, er en matematisk funktion, der returnerer tegnet for et reelt tal. Det angiver, om tallet er positivt, negativt eller nul.

Trigonometriske funktioner

Trigonometriske funktioner er matematiske funktioner, der relaterer vinklerne i en retvinklet trekant til længden af ​​dens sider. De seks primære trigonometriske funktioner er sinus (sin), cosinus (cos), tangent (tan), cosecans (cosec), secant (sek) og cotangens (cot).

Komplekse funktioner

Enhver funktion, hvor inputvariablen er kompleks funktion, kaldes den komplekse funktion. Et komplekst tal er et tal, der kan plottes på det komplekse plan. I en komplekst tal vi har reelt tal og imaginært tal. Et komplekst tal(z) er repræsenteret som z= x + iy og en kompleks funktion er repræsenteret som f(z) = P(x, y) + iQ(x, y)

Anvendelser af funktioner

Når vi siger, at en variabel mængde y er en funktion af en variabel mængde x, angiver vi, at y er afhængig af x, og at y's værdi er bestemt af x's værdi. Denne afhængighed kan udtrykkes som følger: f = y (x).

• Radius af en cirkel kan bruges til at beregne arealet af en cirkel. Radius r påvirker område A. Vi erklærer, at A er en funktion af r i funktionernes matematiske sprog. Vi kan skrive A = f(r) =π×r²
• En kugles volumen V er en funktion af dens radius. V = f(r) = 4/3×r³angiver afhængigheden af ​​V af r.
• Kraft er en funktion af accelerationen af ​​et legeme med fast masse m. F = g(a) = m×a.

Folk læser også:

• Relation og funktion
  
• Domæne og række af trigonometriske funktioner
• Rækkevidde af en funktion
• Hyperbolsk funktion

Eksempler på funktion

Eksempel 1: For to funktioner er f og g defineret som f(x) = x ² og g(x) = ln(2x). Find den sammensatte funktion (gof )( x )

Løsning:

Givet:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f(x))

= ln(2x²)

= 2 ln(√2x)

Således, (gof)(x) = 2 ln(√2x)

Eksempel 2: Find output af funktionen g(t)= 6t ² + 5 kl

• (i) t = 0
• (ii) t = 2

Løsning:

Givet funktion,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Eksempel 3: Længden af ​​et rektangel er fem gange dets bredde, udtryk arealet af rektanglet som funktion af dets længde.

Løsning:

Lad, længden af ​​rektanglet være l og bredden af ​​rektanglet er b

Nu,

• b = l/5

Areal af rektangel(A) = l × l/5 = l²/5

Således er rektanglets område som funktionen af ​​dets længde,

A(l) = l ² /5

Øv problemer om, hvad der er en funktion

1. Givet funktionen f(x)=3x+5

• Find f(2)
• Find f(−1)
• Bestem funktionens domæne og rækkevidde.

2. Givet funktionen g(x)=x ² – 4x + 3

hvad er maven

• Find rødderne til funktionen.
• Find g(3) og g(0).
• Bestem toppunktet for funktionen.

3. Givet to funktioner f(x)=x + 2 og h(x)=2x – 3

• Find den sammensatte funktion (f ∘ h) (x)
• Evaluer (f ∘ h)(2)

Resumé – Hvad er en funktion

En funktion i matematik er en særlig relation mellem inputværdier (domæne) og outputværdier (interval), hvor hvert input er forbundet med et unikt output. Repræsenteret som y = f(x) har funktioner specifikke karakteristika og kan visualiseres ved hjælp af ordnede par, tabeller eller grafer. De er essentielle i forskellige matematiske problemer og findes i forskellige typer, herunder injektiv (en-til-en), surjektiv (onto) og bijektiv (begge). Funktioner kan testes ved hjælp af den lodrette linjetest og klassificeres yderligere i polynomiske, inverse, eksponentielle, logaritmiske og trigonometriske funktioner. Forståelse af funktioner involverer at genkende deres domæne, rækkevidde og reglerne, der definerer dem. Eksempler inkluderer simple lineære funktioner som y = 2x + 1 og komplekse sammensætninger af funktioner. Funktioner spiller en afgørende rolle i algebra, geometri og calculus og hjælper med repræsentation og analyse af matematiske sammenhænge og fænomener i den virkelige verden.

Ofte stillede spørgsmål om Hvad er en funktion

Hvad er definitionen af ​​en funktion?

En relation f defineret på et sæt A til et andet sæt B kaldes en funktion i matematik, hvis hver værdi af A har en unik værdi i sæt B.

Hvordan skriver man en funktion i matematik?

Funktionen f i matematik er repræsenteret som f: A → B og er defineret som, f(x) = x + 2. Her, for hver unik værdi af x, har vi en unik værdi af y.

Hvordan transformerer man en funktion?

Vi kan nemt transformere en funktion til andre funktioner ved blot at udføre grundlæggende algebraiske operationer på funktionen. Funktionens forskellige transformation er refleksion, translation, rotation osv.

Hvad er en rationel funktion?

En brøkfunktion, hvor tælleren og nævneren er polynomielle funktioner, kaldes den rationelle funktion. Nogle eksempler på den rationelle funktion er,

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), etc.

Hvad er en lineær funktion?

En algebraisk funktion, hvor hvert led i funktionen enten er konstant eller har en potens af én, kaldes en lineær funktion. Nogle eksempler på den lineære funktion er,

• f(x) = 2x + 3
• g(x) = x – 5 osv.

Hvad er domæne og codomæne for en funktion?

Hvis vi definerer funktionen som, y = f(x). Så er domænet for x alle værdierne af x, for hvilke y resulterer i en unik værdi. Og co-domænet af y er sættet af alle værdierne af y for hver værdi af x.

Hvordan identificerer man en funktion i matematik?

Hvis en inputværdi (x) af domænet i en relation har mere end ét billede (y), kan disse relationer aldrig være en funktion. Så hvis værdien af ​​x gentages i det ordnede par, er det aldrig en funktion.