Komplekse tal er den naturlige fortsættelse af reelle tal. I den moderne tidsalder bruges komplekse tal på mange områder, såsom digital signalbehandling, kryptografi og mange computerrelaterede felter.

I denne artikel lærer vi om imaginære tal, komplekse tal og dets type, forskellige operationer på komplekse tal, egenskaber ved komplekse tal, anvendelse af komplekse tal osv.

Definition af komplekse tal

Komplekse tal er tal af formularen (a + i b) hvor -en & b er de reelle tal og jeg er en imaginær enhed kaldet iota, der repræsenterer √-1. For eksempel er 2 + 3i et komplekst tal, hvor 2 er et reelt tal, og 3i er et imaginært tal. Komplekse tal kan skrives som a + ib, hvor a og b er rationelle tal, som kan repræsenteres på en tallinje, der strækker sig til uendelighed .

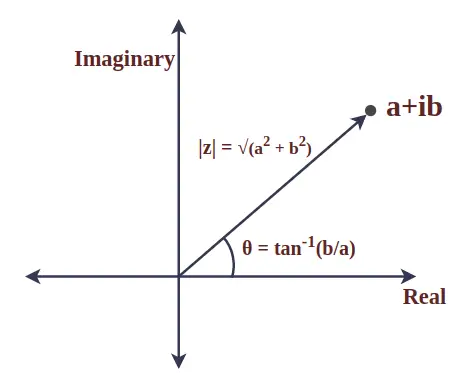
Modulus af komplekst tal

Modulus af det komplekse tal er den absolutte værdi og repræsenterer afstanden mellem oprindelsen og det givne punkt. Det er også kendt som størrelsen af ​​det komplekse tal. Lad os betragte et komplekst tal z = a + ib, så er modulus af z defineret som:

|z| = √(a ² + b ² )

hvor,

• -en er den reelle del af det komplekse tal z, og
• b er den imaginære del af det komplekse tal z.

Argument for komplekst tal

Vinklen mellem radiusvektoren for et komplekst tal og den positive x-akse kaldes argumentet for et komplekst tal. For et komplekst tal z = a + ib er det matematisk givet ved:

θ = tan ^-1 (b/a)

hvor,

• -en er den reelle del af det komplekse tal z, og
• b er den imaginære del af det komplekse tal z.

Power of i(iota)

i(iota) er defineret som kvadratroden af ​​-1. Enhver potens af i kan således udtrykkes som en gentagen multiplikation af i af sig selv, dvs.

• i = √(-1)
• jeg²= -1
• jeg³= – jeg
• jeg⁴= 1
• jeg⁵= i
• jeg⁶= – 1
• og så videre..

Behov for komplekse tal

I oldtiden havde man kun viden om naturlige tal som disse tal er mest intuitive af natur, da den menneskelige hjerne allerede har en forståelse af dem ved hjælp af billeder af ting som får og mad. Vi har således kun mængden af ​​naturlige tal ( N ) men i naturlige tal er der ingen løsning på ligningen x + a = b (a> b) og a, b ∈ N. Således opstod en forlængelse af naturlige tal, dvs. Heltal( jeg ).

Nu, igen i dette talsæt, er der ingen løsning på ligningen, ax = b (a ≠ 0) og a, b ∈ I, hvor a og b begge er heltal. Således udvides et sæt af heltal (I) til et sæt rationelle tal ( Q ).

Igen, i dette sæt af rationelle tal er der ingen løsning på ligningen x²= a (a> 0) og a ∈ Q. Således, Q udvides til at omfatte tal således, at x²= a(for a> 0) dvs. irrationelle tal. Dette sæt hedder Real Numbers og er repræsenteret af R .

Nu har man i lang tid troet, at vi ikke behøver at udvide dette sæt af reelle tal for at danne endnu et større sæt, da denne samling af tal synes komplet. Men igen opstod et nyt problem i dette sæt af tal, dvs. der er ikke noget reelt tal, således at x²= a (a <0) og a ∈ R. Således udvides mængden af ​​reelle tal yderligere til at omfatte alle sådanne værdisatte og navngivne dette sæt komplekse tal og er repræsenteret af C .

Klassificering af komplekse tal

Som vi ved er standardformen for et komplekst tal z = (a + i b) hvor a, b ∈ R, og i er iota (en imaginær enhed). Så afhængigt af værdierne af a (kaldet reel del) og b (kaldet imaginær del), er de komplekse tal klassificeret i fire typer:

• Nul komplekst tal
• Rent rigtige tal
• Rent imaginære tal
• imaginære tal

Lad os lære om disse typer i detaljer.

Nul komplekst tal

For ethvert komplekst tal z = a + ib, hvis a = 0 & b = 0, kaldes det komplekse tal nul komplekst tal. For eksempel er det eneste eksempel på dette 0.

Rent rigtige tal

For ethvert komplekst tal z = a + ib, hvis a ≠ 0 & b = 0, så kaldes det komplekse tal et rent reelt tal, dvs. et tal uden nogen imaginær del. Alle de reelle tal er eksempler på dette, således at 2, 3, 5, 7 osv.

Rent imaginære tal

For ethvert komplekst tal z = a + ib, hvis a = 0 & b ≠ 0, så kaldes et komplekst tal et rent imaginært tal, dvs. et tal uden reel del. Alle tal uden reelle dele er eksempler på denne type tal, dvs. -7i, -5i, -i, i, 5i, 7i osv.

imaginære tal

For ethvert komplekst tal z = a + ib, hvis a ≠ 0 & b ≠ 0, så kaldes et komplekst tal et imaginært tal . For eksempel (-1 – i), (1 + i), (1 – i), (2 + 3i) osv.

sorteret arraylist i java

Forskellige former for komplekse tal

Der er forskellige former for komplekse tal, der er,

• Rektangulær Form
• Polar Form
• Eksponentiel form

Lad os nu lære om dem i detaljer.

Rektangulær Form

Rektangulær Form er også kaldet Standard formular og det er repræsenteret ved (a + ib), hvor a og b er de reelle tal.

For eksempel: (5 + 5i), (-7i), (-3 – 4i) osv.

Polar Form

Polar Form er repræsentationen af ​​et komplekst tal, hvor polære koordinater [hvor koordinater er repræsenteret som (r, θ), hvor r er afstanden fra origo og θ er vinklen mellem linjen, der forbinder punktet og origo og den positive x-akse) bruges til at repræsentere et komplekst tal. Ethvert komplekst tal er repræsenteret som r [cos θ + i sin θ].

For eksempler: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6], osv.

Eksponentiel form

Eksponentielle former for komplekse tal er repræsentationen af ​​komplekse tal ved hjælp af Eulers formel og i denne form er komplekse tal repræsenteret ved re^jeg, hvor r er afstanden af ​​et punkt fra origo, og θ er vinklen mellem den positive x-akse og radiusvektor.

For eksempel: eⁱ⁽⁰⁾, Det er^i(π/2), 5.e^i(π/6), etc.

Bemærk: Alle tre former for de komplekse tal diskuteret ovenfor er indbyrdes konverterbare, dvs. disse kan konverteres fra en form til en anden meget nemt.

Operationer på komplekse tal

Følgende handlinger kan udføres på komplekse tal:

• Tilføjelse
• Subtraktion
• Multiplikation
• Division
• Konjugation

Tilføjelse af komplekse tal

Vi kan tilføje to komplekse tal ved blot at tilføje deres reelle og imaginære dele separat.

For eksempel (3 + 2i) + (1 + 4i) = 4 + 6i.

Subtraktion af komplekse tal

Vi kan trække to komplekse tal fra ved blot at trække deres reelle og deres imaginære dele fra hver for sig.

For eksempel (3 + 2i) – (1 + 4i) = 2 – 2i.

Multiplikation af komplekse tal

Vi kan gange to komplekse tal ved at bruge den distributive egenskab og det faktum, at jeg²= -1.

For eksempel (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Inddeling af komplekse tal

Vi kan dividere et komplekst tal med et andet ved blot at gange både tælleren og nævneren med nævnerens komplekse konjugat og yderligere simplificere udtrykket.

For eksempel (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Konjugering af komplekse tal

Vi kan nemt finde konjugeret af et komplekst tal, ved blot at ændre tegnet på dens imaginære del. Konjugat af et komplekst tal er ofte angivet med en streg over tallet, såsom z̄.

For eksempel er konjugatet af 3 + 2i 3 – 2i.

Identiteter for komplekse tal

For alle to komplekse tal z₁og z₂følgende algebraiske identiteter kan angives:

• (Med ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Med ₁ - Med ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Med ₁ ) ² - (Med ₂ ) ² = (z ₁ + z ₂ )(Med ₁ - Med ₂ )
• (Med ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Med ₂ +3(z ₂ ) ² Med ₁ + (z ₂ ) ³
• (Med ₁ - Med ₂ ) ³ = (z ₁ ) ³ – 3(z ₁ ) ² Med ₂ +3(z ₂ ) ² Med ₁ - (Med ₂ ) ³

Formler relateret til komplekse tal

Der er nogle formler relateret til komplekse tal, hvoraf nogle er som følger:

java er lig

Eulers formel

Eulers formel viser forholdet mellem den imaginære magt af eksponent og trigonometrisk forhold sin og cos og er givet ved:

det er ^ix = cos x + i sin x

De Moivres formel

De Moivres formel udtrykker n^thpotens af et komplekst tal i polær form og er givet ved:

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

Kompleks fly

Planen, hvorpå de komplekse tal er entydigt repræsenteret, kaldes det komplekse plan eller Argand-planet eller Gauss-planet.

Det komplekse plan har to akser:

• X-akse eller reel akse
• Y-akse eller imaginær akse

X-akse eller reel akse

hvis ellers i java

• Alle de rent reelle komplekse tal er entydigt repræsenteret af et punkt på det.
• Den reelle del Re(z) af alle komplekse tal er plottet i forhold til den.
• Derfor kaldes X-aksen også Virkelig akse .

Y-akse eller imaginær akse

• Alle de rent imaginære komplekse tal er entydigt repræsenteret af et punkt på det.
• Den imaginære del Im(z) af alle komplekse tal er plottet i forhold til den.
• Derfor kaldes Y-aksen også Imaginær akse .

Geometrisk repræsentation af komplekse tal

Som vi ved, at hvert komplekst tal (z = a + i b) er repræsenteret af et unikt punkt p(a, b) på den komplekse plan, og hvert punkt på den komplekse plan repræsenterer et unikt komplekst tal.

Følg disse konventioner for at repræsentere et komplekst tal z = (a + i b) på det komplekse plan:

• Den reelle del af z (Re(z) = a) bliver X-koordinaten til punktet p

• Den imaginære del af z (Im(z) = b) bliver Y-koordinaten for punktet p

Og til sidst z (a + i b) ⇒ p (a, b), som er et punkt på det komplekse plan.

Egenskaber for komplekse tal

Der er forskellige egenskaber ved komplekse tal, hvoraf nogle er som følger:

• For ethvert komplekst tal z = a + ib, hvis z = 0, så er a = 0 såvel som b = 0.
• For 4 reelle tal a, b, c og d, således at z₁= a + ib og z₂= c + id. Hvis z₁= z₂derefter a = c, og b=d.
• Tilføjelse af et komplekst tal med dets konjugat resulterer i et rent reelt tal, dvs. z + z̄ = reelt tal.

Lad z = a + ib,

z + z̄ = a + en + a – en

⇒ z + z̄ = 2a (som er rent reel)

• Produktet af et komplekst tal med dets konjugerede resultater er også et rent reelt tal, dvs. z × z̄ = reelt tal

Lad da z = a + ib

z × z̄ = (a + en) × (a – en)

⇒ z × z̄= a²– jeg²b²

⇒ z × z̄ = a²+ b²(som er rent ægte)

• Komplekse tal er kommutativ under drift af addition og multiplikation. Lad os betragte to komplekse tal z₁og z₂, og så

Med ₁ +z ₂ = z ₂ +z ₁

Med ₁ × z ₂ = z ₂ × z ₁

• Komplekse tal er associativ med operation af addition og multiplikation. Lad os betragte tre komplekse tal z₁, Med₂og z₃derefter

(Med ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Med ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Komplekse tal holder fordelingsejendom også multiplikation over addition. Lad os betragte tre komplekse tal z₁, Med₂og z₃derefter

Med ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Læs mere,

• Opdeling af komplekse tal
• Z-bjælke i komplekse tal

Eksempler på komplekse tal

Eksempel 1: Plot disse komplekse tal z = 3 + 2i på det komplekse plan.

Løsning:

Givet:

Med = 3 + 2 i

Så punktet er z(3, 2). Nu plotter vi dette punkt på nedenstående graf, her i denne graf repræsenterer x-aksen den reelle del og y-aksen repræsenterer den imaginære del.

Eksempel 2: Plot disse komplekse tal z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) på det komplekse plan.

Løsning:

Givet:

Med₁= (2 + 2 i)

Med₂= (-2 + 3 i)

Med₃= (-1 – 3 i)

Med₄= (1 – i)

Så punkterne er z₁(2, 2), z₂(-2, 3), z₃(-1, -3) og z₄(1, -1). Nu plotter vi disse punkter på nedenstående graf, her i denne graf repræsenterer x-aksen den reelle del og y-aksen repræsenterer den imaginære del.

linux task manager

Ofte stillede spørgsmål om komplekse tal

Definer komplekse tal.

Tal på formen a+ib kaldes komplekst tal, hvor a og b er det reelle tal, og i er den imaginære enhed, der repræsenterer kvadratroden af ​​-1.

Hvad er forskellen mellem et reelt tal og et komplekst tal?

Forskellen mellem reelle og komplekse tal er, at vi kun behøver et tal til at repræsentere et reelt tal, men har brug for to reelle tal for at repræsentere et komplekst tal.

Hvad er den reelle del og den imaginære del af et komplekst tal?

I et komplekst tal a + ib er a den reelle del af det komplekse tal, og b kaldes den imaginære del af det komplekse tal.

Hvad er det komplekse konjugat af et komplekst tal?

For et komplekst tal a + ib kaldes a – ib dets komplekse konjugat. Komplekse konjugater kan findes ved blot at ændre tegnet på den imaginære del.

Hvad er modulet af et komplekst tal?

Afstand mellem oprindelsen og punktet repræsenteret af et komplekst tal i argandplanet kaldes modulet af det komplette tal, og for z = a + ib er det matematisk givet ved:

|z| = √(a ² + b ² )

Hvad er argumentet for et komplekst tal?

Vinklen mellem radiusvektoren for et komplekst tal og den positive x-akse kaldes argumentet for et komplekst tal, og for z = a + ib er det matematisk givet ved:

θ = tan ^-1 (b/a)

Hvad er den polære form af et komplekst tal?

For ethvert komplekst tal, z = a + ib, er den polære form af dette givet ved:

r [cos θ + i sin θ]

Hvad er Eulers formel?

Eulers formel viser forholdet mellem den imaginære magt af eksponent og trigonometrisk forhold sin og cos og er givet ved:

det er ^ix = cos x + i sin x