Enhedscirkel er en cirkel, hvis radius er 1. Enhedscirklens centrum er ved origo(0,0) på aksen. Det omkreds af enhedscirkel er 2π enheder, hvorimod areal af enhedscirkel er π enheder2. Det bærer alle egenskaberne af Circle. Enhedscirkel har ligningen x2+ og2= 1. Denne enhedscirkel hjælper med at definere forskellige trigonometriske begreber.
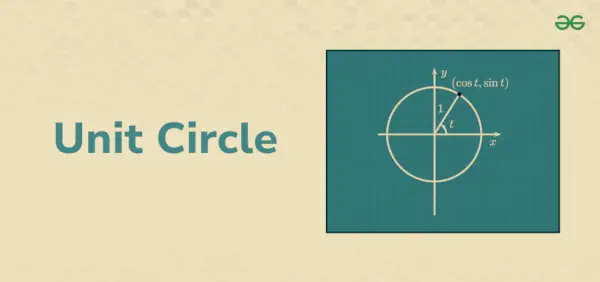
Enhedscirkel
Enhedscirklen betegnes ofte som S1generalisering til højere dimensioner er enhedssfæren. Lad os forstå mere om Unit Circle, Formel og Solved eksempler i detaljer nedenfor.
Hvad er Unit Circle?
Enhedscirkel er en cirkel, der har en radius på En(1) enhed. Vi bruger den kartesiske plan til at tegne en enhedscirkel, og en enhedscirkel er et 2-graders polynomium med to variable. Enhedscirklen har forskellige anvendelser inden for trigonometri og algebra og bruges hovedsageligt til at finde værdierne af forskellige trigonometriske forhold såsom sin x, cos x, tan x og andre.
Definition af enhedscirkel
I matematik definerer vi en enhedscirkel som stedet for et fikspunkt, der er i en afstand af en enhed fra cirklens centrum. En enhedscirkel har en radius på én enhed og deraf navnet enhedscirkel.
Ligning af enhedscirkel
Vi ved, at ligningen for enhver cirkel med centrum (h, k) og radius 'r' er,
(x – h) 2 + (y – k) 2 = r 2
For en enhedscirkel ved vi, at r er 1 enhed, og derfor er ligningen for enhedscirklen,
(x – h) 2 + (y – k) 2 = 1
Formel for enhedscirkel
Hvis centrum af enhedscirklen er oprindelse, dvs. (h, k) = (0, 0), så er ligningen for enhedscirklen,
x 2 + og 2 = 1
En enhedscirkel er repræsenteret i billedet tilføjet nedenfor, med centerkoordinat h, k og når cirklen er ved origo, er værdien af h og k nul, og radius AP er lig med 1 enhed.
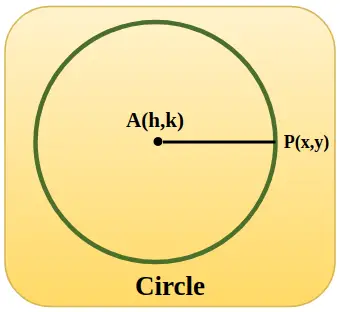
Trigonometriske funktioner ved hjælp af enhedscirkel
Anvendelsen af Pythagoras-sætningen i en enhedscirkel kan bedre bruges til at forstå trigonometriske funktioner. Til dette betragter vi en retvinklet trekant for at være placeret inde i en enhedscirkel i det kartesiske koordinatplan. Hvis vi bemærker, betegner radius af denne cirkel hypotenusen af den retvinklede trekant.
Cirklens radius danner en vektor. Dette fører til dannelsen af en vinkel, f.eks. θ med den positive x-akse. Lad os antage, at x er grundlængden, og y er højdelængden af henholdsvis den retvinklede trekant. Koordinaterne for radiusvektorens endepunkter er (x, y) hhv.
Den retvinklede trekant holder siderne 1, x og y henholdsvis. Det trigonometriske forhold kan nu beregnes som følger:
sin θ = Højde/Hypotenuse = y/1
cos θ = Base/Hypotenuse = x/1
konverter fra streng til heltal java
Nu,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Ved at erstatte værdierne af θ kan vi få hovedværdier for alle trigonometriske funktioner. Tilsvarende findes værdier af trigonometriske funktioner ved forskellige værdier.
Unit Circle med Sin Cos og Tan
Ethvert punkt på enhedscirklen med koordinaterne (x, y) er repræsenteret ved hjælp af trigonometriske identiteter som, (cosθ, sinθ). Koordinaterne for radiushjørnerne repræsenterer cosinus og sinus af θ-værdierne for en bestemt værdi af θ og radiuslinjen. Vi har cos θ = x, og sin θ = y. Der er fire dele af en cirkel, der hver ligger i en kvadrant, hvilket giver en vinkel på 90°, 180°, 270° og 360°. Radiusværdierne ligger mellem -1 til 1 hhv. Også sin θ og cos θ værdierne ligger mellem henholdsvis 1 og -1.
Enhedscirkel og trigonometriske identiteter
Enhedscirklens trigonometriske identiteter for cotangens, secant og cosecant kan beregnes ved hjælp af identiteterne for sin, cos og tan. Afslutningsvis får vi en retvinklet trekant med siderne henholdsvis 1, x og y. Beregning af enhedscirkelidentiteterne kan udtrykkes som,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- sek θ = 1/x
- cosec θ = 1/y
- barneseng θ = x/y
Enhedscirkeldiagram
Enhedscirkeldiagrammet er et diagram, der indeholder værdien af den trigonometriske funktion sinus og cosinus for forskellige vinkler. Enhedscirkeldiagrammet for det samme tilføjes nedenfor,
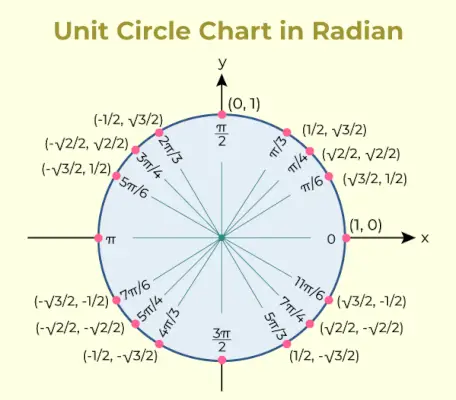
Enhedscirkelbord
De trigonometriske forhold, der bruges i enhedscirkeltabellen, bruges til at angive koordinaterne for de punkter på enhedscirklen, der svarer til fælles vinkler.
| Vinkler | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| uden | 0 | 1/2 | 1/√(2) avl træ | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| så | 0 | 1/√(3) | 1 | √(3) numpy dot produkt | Ikke defineret |
| csc | Ikke defineret | 2 | √(2) | 23) | 1 |
| sek | 1 | 23) | √(2) | 2 | Ikke defineret |
| barneseng | Ikke defineret | √(3) | 1 | 1/√(3) | 0 |
Enhedscirkel Pythagoras identiteter
Der er tre pythagoræiske identiteter, og alle kan nemt bevises ved hjælp af konceptet med enhedscirklen, de tre pythagoræiske identiteter er,
- uden2θ + cos2θ = 1
- 1 + så2θ = sek2jeg
- 1 + barneseng2θ = cosec2jeg
Unit Circle Complex Plane
Komplekse tal og Complex Plane er let forklaret ved hjælp af konceptet enhedscirkel. Ligningen for enhedscirkel i kompleks form er,
|z| = 1
fordele og ulemper ved teknologiELLER
x 2 + og 2 = 1
I Eulers form er komplekst tal repræsenteret som,
z = e det = cos t + i(sin t)
Læs mere
Løste eksempler på enhedscirkel
Q1: Bevis at punktet Q ligger på en enhedscirkel, Q = [1/√(6), √4/√6]
Løsning:
givet,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Ligning af enhedscirkel er,
x2+ og2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Punkt Q[1/√(6), √4/√6] ligger således ikke på enhedscirklen.
Q2: Beregn så 30 O ved hjælp af sin- og cos-værdierne for enhedscirklen.
Løsning:
tan 30° ved hjælp af sin- og cos-værdier,
solbrun 30° = (synd 30°)/ (cos 30°)
- uden 30° = 1/2
- cos 30° = √(3)/2
solbrun 30° = 1/2/√(3)/2
java mainsolbrun 30° = 1/√(3)
Q3: Bekræft om punktet P [1/2, √(3)/2] ligger på enhedscirklen.
Løsning:
givet,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Ligning af enhedscirkel er,
- x2+ og2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Øvelsesspørgsmål om Unit Circle
Q1. Kontroller, om punkterne A (1/2, 3/2) ligger på en enhedscirkel.
Q2. Kontroller, om punkterne A (2, 1/2) ligger på en enhedscirkel.
Q3. Find værdien af cos 240°
Q4. Find værdien af tan 320°
Q5. Find værdien af sin 160°
Unit Circle – ofte stillede spørgsmål
Hvad er Unit Circle?
En enhedscirkel er defineret som placeringen af et punkt én enhed væk fra et fast punkt. Den har et centrum ved (0,0) og værdien af dens radius er 1.
Hvordan kontrollerer man, om et punkt ligger på enhedscirklen?
Ethvert punkt, der ligger i et 2D-plan, der har formen (x, y), sættes i enhedscirkelligningen x2+ og2= 1 for at kontrollere, om den ligger på cirklen eller ej.
Hvad er formlen for enhedscirkel?
Enhedscirkelformlen er en formel, der bruges til at repræsentere en enhedscirkel algebraisk. Enhedscirkelformlen er givet som,
x 2 + og 2 = 1
Hvorfor kaldes det Unit Circle?
En enhedscirkel kaldes enhedscirkel, fordi den har en radius på en(1) enheder.
