Først vil vi forstå binært træ og binært søgetræ separat, og så vil vi se på forskellene mellem et binært træ og et binært søgetræ.

Hvad er et binært træ?

EN Binært træ er enPointer til venstre barn:Den gemmer referencen for venstre-under-knudepunktet.Pointer til det rigtige barn:Den gemmer referencen for højre-under-knuden.Dataelement:Dataelementet er værdien af ​​de data, som er lagret af noden.

Det binære træ kan repræsenteres som:

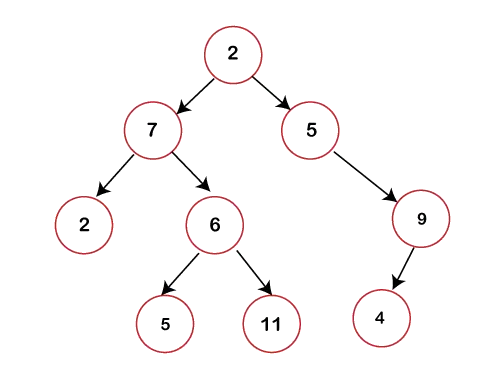
I ovenstående figur kan vi observere, at hver node indeholder højst 2 børn. Hvis en node ikke indeholder venstre eller højre underordnede, vil værdien af ​​markøren i forhold til det underordnede være NULL.

Grundlæggende terminologier brugt i et binært træ er:

Rodknude:Rodnoden er den første eller den øverste knude i et binært træ.Overordnet node:Når en node er forbundet til en anden node gennem kanter, er den node kendt som en overordnet node. I et binært træ kan forældreknudepunktet maksimalt have 2 børn.Barneknude:Hvis en node har sin forgænger, er den node kendt som en børneknude .Bladknude:Noden, som ikke indeholder et barn kendt som en bladknude .Intern knude:Noden, der har mindst 2 børn kendt som en intern knude .Dybde af en node:Afstanden fra rodknuden til den givne knude er kendt som a dybden af ​​en knude . Vi leverer etiketter til alle noderne, ligesom rodknude er mærket med 0, da den ikke har nogen dybde, børn af rodknudepunkter er mærket med 1, børn af rodbarn er mærket med 2.Højde:Den længste afstand fra rodknuden til bladknuden er højden af ​​noden .

I et binært træ er der ét træ kendt som et perfekt binært træ . Det er en træ, hvor alle de interne noder skal indeholde to noder, og alle bladknuderne skal være i samme dybde. I tilfælde af et perfekt binært træ kan det samlede antal noder, der findes i et binært træ, beregnes ved at bruge følgende ligning:

n = 2^m+1-1

hvor n er antallet af knudepunkter, m er dybden af ​​en knude.

Hvad er et binært søgetræ?

EN Binært søgetræ er et træ, der følger en eller anden rækkefølge for at arrangere elementerne, hvorimod det binære træ ikke følger nogen rækkefølge. I et binært søgetræ skal værdien af ​​den venstre node være mindre end den overordnede node, og værdien af ​​den højre node skal være større end den overordnede node.

Lad os forstå konceptet med et binært søgetræ gennem eksempler.

I ovenstående figur kan vi observere, at værdien af ​​rodknuden er 15, hvilket er større end værdien af ​​alle knuderne i det venstre undertræ. Værdien af ​​rodknude er mindre end værdierne af alle knudepunkter i et højre undertræ. Nu flytter vi til venstre underordnede af rodnoden. 10 er større end 8 og mindre end 12; det opfylder også egenskaben for det binære søgetræ. Nu flytter vi til det højre underordnede af rodknuden; værdien 20 er større end 17 og mindre end 25; det opfylder også egenskaben for binært søgetræ. Derfor kan vi sige, at træet vist ovenfor er det binære søgetræ.

Nu, hvis vi ændrer værdien af ​​12 til 16 i ovenstående binære træ, skal vi finde ud af, om det stadig er et binært søgetræ eller ej.

Værdien af ​​rodnoden er 15, hvilket er større end 10, men mindre end 16, så det opfylder ikke egenskaben for det binære søgetræ. Derfor er det ikke et binært søgetræ.

Operationer på binært søgetræ

Vi kan udføre indsættelses-, sletnings- og søgeoperationer på det binære søgetræ. Lad os forstå, hvordan en søgning udføres på en binær søgning. Det binære træ er vist nedenfor, som vi skal udføre søgeoperationen på:

Antag, at vi skal søge 10 i ovenstående binære træ. For at udføre den binære søgning vil vi overveje alle heltal i et sorteret array. Først opretter vi en komplet liste i et søgeområde, og alle numre vil eksistere i søgeområdet. Søgerummet er markeret med to pointere, dvs. start og slut. Arrayet i ovenstående binære træ kan repræsenteres som

Først vil vi beregne det midterste element og sammenligne det midterste element med det element, som skal søges. Det midterste element beregnes ved at bruge n/2. Værdien af ​​n er 7; derfor er det midterste element 15. Det midterste element er ikke lig med det søgte element, dvs. 10.

Bemærk: Hvis elementet, der søges efter, er mindre end det midterste element, vil søgningen blive udført i venstre halvdel; ellers vil søgningen blive udført på højre halvdel. Ved ligestilling findes elementet.

Da det element, der skal søges i, er mindre end det midterste element, vil søgningen blive udført på venstre array. Nu er søgningen reduceret til det halve, som vist nedenfor:

Midtelementet i venstre array er 10, hvilket er lig med det søgte element.

Tidskompleksitet

I en binær søgning er der n elementer. Hvis det midterste element ikke er lig med det søgte element, reduceres søgerummet til n/2, og vi bliver ved med at reducere søgerummet med n/2, indtil vi har fundet elementet. I hele reduktionen, hvis vi flytter fra n til n/2 til n/4 og så videre, vil det tage log₂n trin.

Forskelle mellem binært træ og binært søgetræ