TRIGONOMETRI TABEL

Trigonometri tabel er en standardtabel, der hjælper os med at finde værdierne af trigonometriske forhold for standardvinkler såsom 0°, 30°, 45°, 60° og 90°. Det består af alle seks trigonometriske forhold: sinus, cosinus, tangens, cosekant, sekant og cotangens.

Lad os lære om trigonometritabellen i detaljer.

Indholdsfortegnelse

Trigonometri tabel
Trigonometriske funktionstabel
Trick til at lære trigonometriske forhold
Sådan husker du trigonometrisk tabel
Sådan opretter du en trig-tabel
Trigonometriske formler
Trigonometriske identitetstabel
Trigonometriske tabeleksempler

Trigonometrisk tabel er arrangementet af værdierne for alle seks trigonometriske funktioner for deres fælles vinkler i en tabelform.

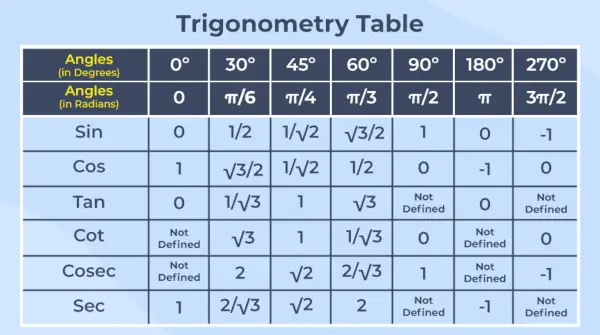
Trigonometri tabel

Bemærk – Trigonometri er en gren af matematikken, der beskæftiger sig med forholdet mellem vinkler og sider af retvinklede trekanter.

Trigonometriske funktionstabel

Trigonometri har 6 grundlæggende trigonometriske funktioner, de er sinus, cosinus, tangent, cosecant, sekant og cotangens. Lad os nu se på de trigonometriske funktioner.

For enhver retvinklet trekant med vinkelret (P), Base (B) og Hypotenuse (H) er de seks trigonometriske funktioner som følger,

Tabel over trigonometriske funktioner
Fungere	Definition	Repræsentation	Forholdet til siderne af en retvinklet trekant
Hans	Forholdet mellem vinkelret og hypotenusen	uden jeg	Modsatte side / Hypotenuse
Cosinus	Forholdet mellem base og hypotenuse	cos jeg	Tilstødende side / Hypotenuse
Tangent	Forholdet mellem sinus og cosinus af en vinkel	så jeg	Modsatte side / Tilstødende side
Cosecant	Gensidig af synd θ	csc jeg eller cosec jeg	Hypotenuse / Modsatte side
Sekant	Gensidig af cos θ	sek jeg	Hypotenuse / Tilstødende side
Cotangens	Gensidig af tan θ	barneseng jeg	Tilstødende side / Modsat side

Bemærk - Trigonometri er en gren af matematikken, der beskæftiger sig med forholdet mellem vinkler og sider af trekanter, især retvinklede trekanter. Det involverer undersøgelse og anvendelse af sinus, cosinus, tangent og andre trigonometriske funktioner til at løse problemer inden for forskellige områder.

Kontrollere : Trigonometri: formler, tabel, identiteter og forhold

Trick til at lære trigonometriske forhold

Studer tabellen diskuteret nedenfor for at lære de trigonometriske forhold på en let at huske måde.

Nogle mennesker har krøllet sort hår for at producere skønhed

sin θ (Nogle) = Vinkelrette(personer) / hypotenuse(har)

cos θ (krøllet) = Base (sort) / hypotenuse (hår)

tan θ (til) = Vinkelret(producer) / Base(skønhed)

Sådan husker du trigonometrisk tabel

Trigonometristabel er ret nem at huske, hvis du kender alle trigonometriformlerne. Der er også et trick kaldet enhånds trick at huske trigonometritabellen.

Sådan husker du trigonometrisk tabel

Trin 1: I figuren ovenfor, for sinustabellen, tæl fingrene på venstre side for standardvinklen.

Trin 2: Divider antallet af fingre på venstre side (beregn i 1. trin) med 4

Trin 3: Find kvadratroden af værdien beregnet i trin 2.

Kontrollere: Trigonometriske formler – Liste over alle trigonometriske identiteter og formler

java design mønstre

Sådan opretter du en trig-tabel

Studer følgende trin for at oprette den trigonometriske tabel for standardvinkler.

Trin 1: Opret tabellen

Lav en tabel og skriv alle vinklerne som f.eks 0°, 30°, 45°, 60° og 90°, i øverste række. Indtast alle trigonometriske funktioner sin, cos, tan, cosec, sec og cot i den første kolonne.

Trin 2: Evaluer værdien for alle vinklerne af sin funktion.

For at finde værdierne af sin funktion skal du dividere 0, 1, 2, 3 og 4 med 4 og tage under roden af hver værdi, henholdsvis som,

For værdien af sin 0° = √(0/4) = 0
Tilsvarende
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1

uden 0°	uden 30°	uden 45°	uden 60°	uden 90°
0	1/2	1/√2	√3/2	1

Trin 3: Evaluer værdien for alle vinklerne af cos-funktionen

Værdien af cos-funktionen er den modsatte af værdien af sin-funktionen, dvs. cos 0° = sin 90°, cos 30° = sin 60° og cos 45° = sin 45°, så

cos 0°	30°	45°	60°	90°
1	√3/2	1/√2	1/2	0

Trin 4: Evaluer værdien for alle vinklerne af tan-funktionen

Værdien af tan-funktionen er lig med sin-funktionen divideret med cos-funktionen, dvs. tan x = sin x / cos x. Værdien af alle vinklerne i tan-funktionen beregnes som,

tan 0°= sin 0° / cos 0° = 0/1 = 0, tilsvarende

altså 0°	altså 30°	altså 45°	altså 60°	altså 90°
0	1/√3	1	√3	Ikke defineret

Trin 5: Evaluer værdien for alle vinklerne af cosec-funktionen

Værdien af cosec-funktionen er lig med den reciproke af sin-funktionen. Værdien af cosec 0° opnås ved at tage den reciproke af sin 0°

cosec 0° = 1 / sin 0° = 1 / 0 = Ikke defineret. Tilsvarende

cosec 0°	cosec 30°	cosec 45°	cosec 60°	cosec 90°
Ikke defineret	2	√2	23	1

Trin 6: Evaluer værdien for alle vinklerne af sek-funktionen

Værdien af sek-funktionen er lig med den reciproke af cos-funktionen. Værdien af sek 0° opnås ved at tage den reciproke af cos 0°

sek 0° = 1 / cos 0° = 1 / 1 = 1. Tilsvarende

sek 0°	sek 30°	sek 45°	sek 60°	sek 90°
1	23	√2	2	Ikke defineret

Trin 7: Evaluer værdien for alle vinklerne af barnesengsfunktionen

Værdien af barnesengsfunktionen er lig med den gensidige solbrune funktion. Værdien af barneseng 0° opnås ved at tage den gensidige af tan 0°

tremmeseng 0° = 1 /tan 0° = 1 / 0 = Ikke defineret. Tilsvarende

barneseng 0°	tremmeseng 30°	tremmeseng 45°	tremmeseng 60°	tremmeseng 90°
Ikke defineret	√3	1	1/√3	0

På denne måde kan vi oprette følgende trigonometriske forholdstabel:

Trigonometrisk tabel for grader og radianer
Vinkel (i grader)	Vinkel (i radianer)	Uden	Cos	Så	Cosec	Sec	Barneseng
0°	0	0	1	0	Udefineret	1	Udefineret
30°	s/6	1/2	√3/2	1/√3	2	23	√3
45°	s/4	√2/2	√2/2	1	√2	√2	1
60°	s/3	√3/2	1/2	√3	23	2	1/√3
90°	p/2	1	0	Udefineret	1	Udefineret	0

Trigonometriske formler

Lad os lære om nogle trigonometriske formler relateret til komplementære og supplerende vinkler.

Komplementære vinkler: Vinkelpar, hvis sum er lig med 90°

Supplerende vinkler: Vinkelpar, hvis sum er lig med 180°

Kontrollere: Trigonometriske forhold

Trig-identiteter af komplementære vinkler

Identiteten af komplementære vinkler er baseret på forholdet mellem de trigonometriske funktioner af to vinkler, der summerer op til 90 grader (eller π/2 radianer). Disse er kendt som co-funktion identiteter .

Trigonometrisk funktion	Identitet
Hans	sin(90°- jeg )=cos jeg
Cosinus	cos(90°- jeg )=uden jeg
Tangent	tan(90°− jeg ) = barneseng jeg
Cotangens	barneseng (90°- jeg )=så jeg
Sekant	sek(90°− jeg )=csc jeg
Cosecant	cosec(90°− jeg )=sek jeg

Trig-identiteter af supplerende vinkler

Identiteten af supplerende vinkler relaterer sig til de trigonometriske funktioner af to vinkler, der summerer op til 180 grader (eller π radianer).

Trigonometrisk funktion	Identitet
Hans	sin(180°− jeg )=uden jeg
Cosinus	cos(180°- jeg )=−cos jeg
Tangent	solbrun (180°− jeg )=−tan jeg
Cotangens	tremmeseng (180°- jeg )=−sengeseng jeg
Sekant	sek(180°− jeg )=−sek jeg
Cosecant	cosec(180°− jeg )=cosec jeg

Trigonometriske identitetstabel

Trigonometriske identiteter er de identiteter, der er meget brugt til at løse trigonometriske problemer. Der er forskellige trigonometriske identiteter, men de tre vigtigste trigonometriske identiteter er,

Tabel over trigonometriske identiteter
Trigonometrisk identitet	Formel
Pythagoras identitet	uden²θ + cos²θ = 1
Sekant-tangent identitet	sek²θ – altså²θ = 1
Cosecant-Cotangens Identity	cosec²θ – barneseng²θ = 1

Tjek også:

Trigonometriske forhold

Omvendte trigonometriske identiteter

Højder og afstande

Trigonometriske tabeleksempler

Lad os løse nogle spørgsmål om den trigonometriske tabel.

Eksempel 1: Hvis sin θ = 4/5, så find alle de trigonometriske værdier.

Løsning:

Her har vi,
vlc for at downloade youtube-videoer

sin θ = 4/5

som, sin θ = Vinkelret / Hypotenus

så vi har vinkelret (P)= 4 og hypotenusen (H) = 5

Altså ifølge Pythagoras sætning H ² = P ² +B ²

Lad os finde ud af værdien af base (B)

5²= B²+ 4²
25 = B²+ 16
25 -16 = B²
B²= 9
B = 3

Nu har vi,
erstatte en farve i gimp

Sin θ = Vinkelret/Hypotenus
= AB/AC = 4/5

Cosinus θ = Base/Hypotenuse
= BC/AC = 3/5

Tangent θ = Vinkelret/Base
= AB/BC = 4/3

Cosecant θ = Hypotenuse/Perpendikulær
= AC/AB = 5/4

Secant θ = Hypotenuse/Base
= AC/BC = 5/3

Cotangens θ = Base/Perpendikulær
= BC/AB = 3/4

Eksempel 2: Find værdien af cos 45° + 2 sin 60° – tan 60°.

Løsning:

Fra trigonometritabellen,

cos 45° = 1/√2, sin 60° = √3/2 og tan 60° = √3

Dermed,

cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2

Eksempel 3: Find værdien af cos 75°.

Løsning:

Vi ved det,

cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2

cos 75°= (√3 – 1)/2√2.

Konklusion - Trigonometri tabel

Trigonometritabellen giver en omfattende reference for de trigonometriske funktioner sinus, cosinus, tangent, cosecant, sekant og cotangens sammen med deres respektive værdier for forskellige vinkler. jeg t fungerer som et værdifuldt værktøj til løsning trigonometriske ligninger, analyse af geometriske sammenhænge og forståelse af periodiske fænomeners adfærd. Uanset om i matematik, fysik, teknik eller andre områder, trigonometritabellen hjælper med beregninger, problemløsning og visualisering og bidrager til en dybere forståelse af trigonometriske begreber og deres anvendelser i scenarier i den virkelige verden.