det Cosinus funktion eller den cos funktion er kort fortalt en af ​​de seks Trigonometriske funktioner grundlæggende for trigonometri. Cosinus i trigonometri er givet som forholdet mellem basen og hypotenusen i en retvinklet trekant. Cosinusfunktion er repræsenteret som Cos x hvor x er den vinkel, som cosinusforholdet beregnes for. Med hensyn til funktion kan vi sige, at x er input eller domæne for cosinusfunktionen.

Det er flittigt brugt i en bred vifte af emner som fysik, geometri og teknik blandt andet generelt ved at udnytte dets periodiske karakter. For eksempel bruges det til at definere lydbølgers bølgekarakter, beregninger af elektrisk flux gennem en plan overflade osv. I denne artikel lærer vi i detaljer om, hvad der er cosinusfunktion, dvs. domæne og rækkevidde af cosinusfunktionen, perioden og grafen for cosinusfunktionen.

Indholdsfortegnelse

• Hvad er cosinusfunktionen?
• Cos i enhedscirkel
• Cosinus funktionsgraf
• Omvendt af cosinusfunktion
• Cosinus funktion i beregning
• Cos Funktionsidentiteter

Hvad er cosinusfunktionen?

Cosinusfunktion er en trigonometrisk funktion, som grundlæggende er periodisk i naturen. Cosinusfunktion udtrykkes som cos x hvor x er en af ​​de spidse vinkler i en retvinklet trekant. Cosinusfunktion finder forholdet mellem base og hypotenusa for en given værdi af x. Cosinusfunktionen forkortes som cos(x) eller cos(θ), hvor x er vinklen i radianer og theta θ er vinklen i grader generelt. Cosinusfunktionen kan defineres ved hjælp af en enhedscirkel, dvs. en cirkel med enhedsradius, som vi vil se senere i denne artikel. Det er periodisk i naturen og gentager sine værdier efter hver fuldstændig rotation af vinkler. På et kartesisk plan kan det omtales som vektorkomponenten af ​​hypotenusen parallelt med x-aksen.

Definition af cosinusfunktion

Cosinusfunktionen er defineret i en retvinklet trekant som forholdet mellem længden af ​​den side, der støder op til den pågældende vinkel, og længden af ​​hypotenusen. Matematisk er Cosinus Funktion givet som

Cos x = Cos θ = Længde af base/længde af hypotenus = b/h = OB/OA

hvor x er vinklen i radianer, og θ er den ækvivalente vinkel i grader.

Domæne og rækkevidde af Cos-funktion

Vi ved, at for en funktion er domæne de tilladte inputværdier, og range er outputværdien for den pågældende input- eller domæneværdi. Derfor kan vi antage, at funktionen fungerer som en processor, der tager input, behandler det og giver et bestemt output. Cos-funktionens domæne og rækkevidde diskuteres nedenfor:

• Domæne for cosinusfunktion: R dvs. sæt af alle reelle tal.
• Cosinusfunktionsområde: [-1, 1], dvs. output varierer mellem alle reelle tal mellem -1 og 1.

Periode for en cosinusfunktion

Det fungere er periodisk af natur, dvs. den gentager sig selv efter 2π eller 360°. Med andre ord, det gentager sig selv efter hver fuldstændig rotation. Derfor er perioden for cosinusfunktionen en fuldstændig rotation eller en vinkel på 360° (eller 2π).

Gensidig af en cosinusfunktion

Det reciproke af en cosinusfunktion er kendt som sekant funktion eller sek for kort. Matematisk er den reciproke af cosinusfunktion givet som

git status -s

sek(θ) = 1/cos(θ)

I henhold til reglerne for Gensidige , hvis vi multiplicerer Cos x med Sec x, vil produktet altid være 1.

Cosinus funktionsgraf

Grafen for cosinusfunktionen ligner grafen for sinusfunktionen med en grundlæggende forskel, at for x = 0 passerer sin funktionsgraf fra origo, mens ved x = 0 går cosinusfunktionsgrafen fra (0, 1) ved y-aixs. Følgende er grafen for værdien af ​​cosinusfunktionen, dvs. y = cos x

Egenskaberne diskuteret ovenfor kan ses i grafen ligesom den periodiske karakter af funktionen.

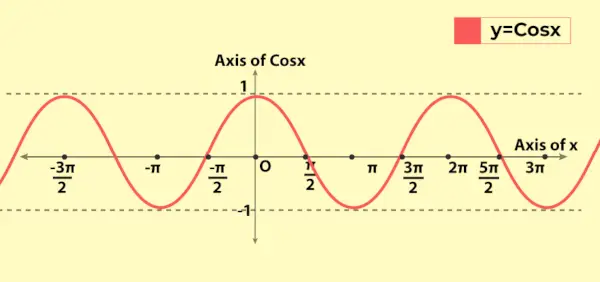
Variation af cosinusfunktion i graf

Da området for cosinusfunktionen er [-1, 1], varierer det derfor fra -1 til 1 i grafen. Det udviser sin periodiske natur, da grafen gentages efter hver længde 2π på x-aksen. Dette afspejler, at cosinusfunktionen har en periode på 2π (eller 360°).

Cos i enhedscirkel

Cosinus Funktion kan defineres ved hjælp af enhedscirkel. Lad os forstå, hvordan vi kan definere cosinusfunktion i form af enhedscirkel.

Overvej et linjestykke OA, der roterer omkring punktet O, hvor O er udgangspunktet for det kartesiske plan. Rotationen af ​​OA beskriver således en enhedscirkel (cirkel af enhedsradius) centreret ved origo O og punktet A ligger altid på denne cirkel. Hvis vi dropper en vinkelret fra A på x-aksen og kalder skæringspunktet for B, og θ er den vinkel OA laver med x-aksens positive retning, så er cos(θ) = projektion af hypotenusen på x -akse = OB/|OA| = OB (da |OA| = 1 enhed).

Bemærk, at retningen OB er vigtig som det ses i de følgende figurer. Det grønne segment angiver længden/størrelsen, og pilen angiver retningen (+ve eller -ve) af cos(θ)

Bemærk, at værdien af ​​cos(θ) er positiv for θ, der tilhører første og fjerde kvadrant, mens negativ for θ, der tilhører anden og tredje kvadrant.

Omvendt af cosinusfunktion

Det omvendte af en cosinusfunktion kendt som bue-cosinus funktion og forkortet som arccos(x) eller cos ^-1 (x) er defineret som følger

cos(x) = y

⇒ cos ^-1 (y) = x

Domæne og rækkevidde af invers cosinusfunktion

Domænet og området for invers cosinusfunktion er nævnt nedenfor:

• Domæne med omvendt cosinusfunktion: Alle reelle tal i området [-1, 1]
• Omfang af invers cosinusfunktion: Alle reelle tal i området [0, π]

Hyperbolsk cosinusfunktion

Hyperbolske funktioner er analoge ækvivalenter til trigonometrisk funktion, hvis algebraiske udtryk er i form af eksponentiel funktion. Den hyperbolske cosinusfunktion forkortet som cosh(x) hvor x er en hyperbolsk vinkel er et koncept for hyperbolsk geometri. Ligesom (cos(x), sin(x)) repræsenterer et punkt på en enhedscirkel, (cosh(x), sinh(x)) repræsenterer et punkt på en enhedshyperbel, dvs. xy = 1 hvor sinh(x) repræsenterer hyperbolsk sinus funktion. Den algebraiske udvidelse af hyperbolsk cos-funktion er givet som

cosh(x) = (e ^x + og ^-x )/2

Flere detaljer om hyperbolske funktioner er uden for rammerne af denne artikel, men du kan henvise til denne artikel .

Cosinus funktion i beregning

Den gren af ​​calculus i matematik beskæftiger sig med differentiering og integration af en given funktion. Funktionsdifferentiering er ændringshastigheden i funktionen i forhold til den uafhængige variabel, mens integration er den omvendte differentieringsproces, der handler om at finde integralet af en funktion, hvis afledte eksisterer.

Afledt af cosinusfunktion

Det afledte af cosinusfunktion er lig med minus af sinusfunktion. Matematisk

d(cos(x))/dx = -sin(x)

Integration af cosinusfunktion

Det ubestemt integral af cosinusfunktionen er lig med sinusfunktionen. Matematisk -

∫cos(x)dx = sin(x) + C, hvor C er integrationskonstanten.

Sinus- og Cosinusfunktioner

Følgende graf repræsenterer nøgleforskellen mellem både sinus- og cosinusfunktion:

Forskellen mellem sinus- og cosinusfunktioner

Følgende tabel viser forskellene mellem sinus- og cosinusfunktion –

Cos værdi tabel

Følgende tabel giver værdierne af cosinusfunktion for nogle almindelige vinkler i den første kvadrant af kartesisk plan -

Vi kan nemt beregne værdierne af andre almindelige vinkler som 15°, 75°, 195°, -15° osv. ved at bruge disse værdier ved at bruge formlerne cos (x + y) og cos (x – y) beskrevet senere i dette artikel.

Kontrollere, Trigonometrisk bord

Cos Funktionsidentiteter

De grundlæggende trigonometriske identiteter relateret til cosinusfunktion er nævnt nedenfor:

• uden²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/sek(x)
• cos 2x = cos²x – synd²x = 1 – 2sin²x = 2cos²x – 1 = (1 – tan²x/1 + tan²x)
• cos 3x = 4cos³x – 3cos x

relaterede artikler

• Differentiering af trigonometriske funktioner
• Inverse trigonometriske funktioner
• Inverse trig-derivater

Løste eksempler på cosinusfunktion

Her er nogle løste eksempler for at hjælpe dig med bedre at forstå begrebet cosinusfunktion.

Eksempel 1: Hvad er maksimum- og minimumværdierne for cosinusfunktionen?

Løsning:

Den maksimale værdi af cosinusfunktionen er 1 ved 0° og 180°, mens minimumsværdien for funktionen er -1 ved 180°.

Eksempel 2: Ved hvilken(e) vinkler i området [0, 360] er værdien af ​​cosinusfunktionen 0?

Løsning:

Værdien af ​​cosinusfunktionen er 0 ved vinklerne 90° og 270°.

Eksempel 3: For hvilke kvadranter er værdien af ​​cosinusfunktionen negativ?

Løsning:

Cosinusfunktionen er negativ i II^ndog III^rdkvadranter.

Eksempel 4: Beregn værdien af ​​cos (45°).

Løsning:

java returkommando

Som pr. identitet 4 givet ovenfor, cos(-x) = cos(x).

Derfor er cos(-45°) = cos(45°) = 1/√2

Eksempel 5: Beregn værdien af ​​cos(15°).

Løsning:

Brug af identitet 3 angivet ovenfor –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Eksempel 6: Hvad er cos ^-1 (1/2) i området [0,π]?

Løsning:

Lad cos^-1(1/2) = y.

Derfor er cos(y) = 1/2 ⇒ y = π/3 i det ovenfor givne område.

Derfor er svaret π/3.

Eksempel 7: Hvad er værdien af ​​cos(-15°)?

Løsning:

Brug af identitet 3 angivet ovenfor –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternativt kan vi også bruge identiteten cos(-x) = cos(x) og bruge værdien af ​​cos(15°) beregnet i eksempel 5.

Eksempel 8: Beregn arealet under grafen for cosinusfunktionen for x = 0 til x = π/2.

Løsning:

Det givne areal kan beregnes ved at løse følgende bestemte integral –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Derfor er svaret 1 kvadratenhed.

Eksempel 9: Hvis cos(x) = π/3, find værdien af ​​cos(3x) (i decimalform med to decimalcifret præcision).

Løsning:

Brug af identiteten – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Eksempel 10: Find værdien af ​​cos(120°).

Løsning:

Brug af identiteten til cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Praksisspørgsmål: Cos-funktioner

Q1. Hvad er formlen til at beregne cos for en vinkel i en retvinklet trekant?

Q2. Hvad er den geometriske fortolkning af cos på kartesisk plan?

Q3. Beregn værdien af ​​cos(120°).

Q4. Find værdien af ​​cos ^-1 (√3/2) i området [π, 2π].

Q5. Hvis en pæl kaster en skygge af samme længde på jorden, skal du finde solens vinkel i forhold til jorden, hvis solen er i østlig retning.

Resumé – Cosinus funktion

Cosinusfunktionen, betegnet som cos(x), er en grundlæggende trigonometrisk funktion defineret som forholdet mellem basen og hypotenusen i en retvinklet trekant og er essentiel på tværs af forskellige felter som fysik, teknik og geometri på grund af dens periodiske natur , som er medvirkende til modellering af bølgeadfærd. Det har et domæne med alle reelle tal og et område fra -1 til 1, gentager sin cyklus hver 2. Pi radianer eller 360 grader, tydeligt fra dens bølgelignende graf, der starter ved (0,1). Med hensyn til calculus er den afledte af cos(x) − sin( x ), og dets integral giver sin( x )+ C , med C som integrationskonstanten. Denne funktion strækker sig også til hyperbolske former, såsom cosh(x), hvilket forbedrer dens anvendelse i forskellige matematiske sammenhænge og løsninger, herunder bølgeberegninger og svingninger i fysiske systemer.

Cosinus-funktion: ofte stillede spørgsmål

1. Hvad er cosinusfunktion?

Cosinusfunktionen er en af ​​de grundlæggende trigonometriske funktioner. Det er defineret i en retvinklet trekant som forholdet mellem længden af ​​den side, der støder op til den pågældende vinkel, og længden af ​​hypotenusen.

2. Er Cos og Cosinus det samme i trigonometri?

Ja. cos er en forkortelse/kortform af cosinusfunktionen.

3. Hvad er området for Cos-funktionen?

Området for cos- eller cosinusfunktionen er alle reelle tal fra -1 til 1, dvs. [-1,1].

4. Hvad er Domain of Cos-funktionen?

Domænet for cos eller cosinusfunktionen er seren af ​​alle reelle tal, dvs. R .

5. Hvad er den maksimale værdi af Cosinus-funktionen?

Den maksimale værdi af cosinusfunktionen er 1 for alle vinkler svarende til 0° eller 360°.

6. Hvad er minimumsværdien af ​​cosinusfunktionen?

Minimumsværdien af ​​cosinusfunktionen er -1 for alle vinkler svarende til 180°.

7. Hvordan finder man værdien af ​​Cos(-x)?

Værdien af ​​cos(-x) kan beregnes ved at beregne værdien af ​​cos(x) på grund af eksistensen af ​​følgende identitet: cos(-x) = cos(x).

8. Hvordan tegner man Cosinus funktion?

For at tegne grafen for cosinusfunktionen på et kartesisk plan skal du henvise til x-aksen som repræsenterer vinkler i radianer (eller grader) og y-aksen som repræsenterer værdierne af cosinusfunktionen for tilsvarende vinkel på x-aksen. Nu,

• Trin 1: Tag en delmængde af x-aksen, som du gerne vil tegne grafen for.
• Trin 2: Opdel x-aksen i dette område i ækvidistante punkter (dvs. der er lige stor plads mellem alle underpunkterne). Bemærk, at jo større antal delinger, jo større præcision er den resulterende graf.
• Trin 3: For hvert af disse underpunkter x skal du markere punktet (x, cos(x)) på grafen.
• Trin 4: Forbind alle de markerede punkter for at få grafen for cosinusfunktionen (for den delmængde af x-aksen, du valgte).

9. Hvordan finder man perioden for en cosinusfunktion?

Perioden for en cosinusfunktion refererer til det minimumsinterval af værdier, hvorefter funktionen begynder at gentage sig selv. Vi ved, at cosinusfunktionen gentager sig selv efter hver fuldstændig rotation, hvilket betyder 2π radianer. Derfor er perioden for cosinusfunktionen 2π radianer eller 360°.

10. Hvad er amplitude af en cosinusfunktion?

Amplituden af ​​en cosinusfunktion refererer til den maksimale forskydning af værdien af ​​funktionen fra middelpositionen, dvs. x-aksen. Amplituden af ​​cosinusfunktionen er 1, da den maksimale forskydning er 1 (for værdierne -1 og 1 ved henholdsvis 180 og 0 grader. Bemærk, at området for cosinusfunktionen er [-amplitude, amplitude].