Vinklen måles i grader (°) og radianer. Det er dannet mellem de to tilstødende sider af en polygon. Hver polygon har forskellige sider og forskellige antal vinkler. Formlen til at finde vinklerne i grader er nyttig i geometri og trigonometri. Det er vigtigt at forstå andre begreber inden for matematik, såsom bue, en central vinkel på cirklen osv.
- En fuld cirkel = 360°
- En ret linje = 180°
- En halvcirkel = 180°
- En kvart cirkel = 90°
Beregning af vinkler i grader
Der er tre forskellige metoder til at finde vinkler i grader, som er som følger:
- Brug af beskytteren D
- Brug af Pythagoras-sætningen og trigonometrifunktionen i en retvinklet trekant
- Brug af vinkelsummen formlen
- Central vinkel i en cirkel
Brug af beskytteren D
En beskytter er en type lineal eller skala, der bruges til at måle afstand i centimeter eller millimeter. Beskytteren, der bruges til at måle vinkler, er i form af 'D' med værdien af vinkler markeret fra 0 til 180 ° fra begge retninger (højre eller venstre). Vi skal justere aksen med linjen på D for at måle vinklen. Den midterste cirkel af beskytteren er justeret til toppunktet for den vinkel, der måles. Strålerne langs vinkelspidsen hjælper med at finde vinklen i grader.
Brug af Pythagoras-sætningen og trigonometrifunktionen i en retvinklet trekant
I trigonometri er der seks funktioner, sinus, cos, cosec, tan, cot, og sek. En retvinklet trekant har tre sider, base, vinkelret og hypotenusen.
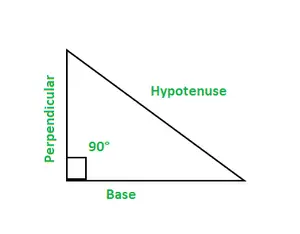
- Base: Det er en tilstødende side til vinklen på 90°. Vinkelret: Det er også en tilstødende side til vinklen på 90°. Hypotenuse: Det er en side modsat vinklen på 90°.
En retvinklet trekant er repræsenteret ved en vinkel på 90° som en af vinklerne. Den samlede sum af vinklen i en trekant er 180°.
- Cosecθ: Det er repræsenteret som hypotenusen divideret med vinkelret.
Cosecθ =
- Cotθ: Det er repræsenteret som base divideret med vinkelret.
Cotθ =
De andre trigonometriske funktioner er repræsenteret som:
sinθ =
Cosθ =
tanθ =
sekθ =
Cosecθ kan også repræsenteres som 1/ sinθ
secθ kan også repræsenteres som 1/ cosθ
alfabet med talCotθ kan også repræsenteres som 1/ tanθ
Hvor,
Θ er vinklen
Pythagoras sætning
Hvis to sider af en ret vinkel er kendt, kan vi nemt beregne den tredje side af en retvinklet trekant. I en retvinklet trekant er Pythagoras sætning givet ved:
(Hypotenuse)2= (Basis)2+ (vinkelret)2
Formel for vinklerum
Vinkelsummen refererer til den samlede sum af indre vinkler af en polygon, der dannes mellem de to sider. Hvis der er seks sider af en polygon, er der omkring seks vinkler. Det hjælper at finde en vinkel, hvis andre vinkler og summen af vinkler af en polygon er kendt.
Formlen til at finde den samlede sum af vinkler af en polygon er givet ved:
Samlet sum af vinkler = 180 (n – 2)
Hvor,
n er antallet af sider af en polygon
Eksempel:
- Hvis n = 4,

Samlet sum af vinkler = 180 (4 – 2)
= 180 (2)
= 360°
Hvis n = 5,
Samlet sum af vinkler = 180 (5 – 2)
= 180 (3)
= 540°
- Hvis n = 6

Samlet sum af vinkler = 180 (6 – 2)
= 180 (4)
= 720°
Central vinkel i en cirkel
En cirkel er en figur med rund form, hvis grænse er lige langt fra dens midtpunkt. Afstanden mellem midtpunktet og grænsen er kendt som cirklens radius. Vinklen dannet af de to radier af cirklen er kendt som den centrale vinkel. Værdien af en cirkels centrale vinkel ligger mellem 0 og 360 grader.

Formlen til at beregne centervinklen af en cirkel er givet ved:
Længde af buen = 2πr × (θ/360)
Θ = 360L/2pr
Hvor,
r er radius af cirklen
AB er buen
Theta er vinklen i grader.
L = Buelængde
Prøveproblemer
Spørgsmål 1: Find den centrale vinkel på en cirkel med en radius på 2m med en buelængde på 4m?
Løsning :
Formlen til at beregne centervinklen af en cirkel er givet ved:
Θ = 360L/2pr
Hvor,
r er radius af cirklen
Theta er vinklen i grader.
L = Buelængde
Θ = Vinkel i grader
r = 2m
L = 4m
Θ = 360 × 4 /2 × π × 2
Θ = 114,6°
Cirklens centrale vinkel er således 114,6°.
Spørgsmål 2: Find den centrale vinkel på en cirkel med en radius på 10 cm med en buelængde på 18 cm?
Løsning :
Formlen til at beregne centervinklen af en cirkel er givet ved:
Θ = 360L/2pr
Hvor,
r er radius af cirklen
Theta er vinklen i grader.
L = Buelængde
r = 10 cm
L = 18 cm
Θ = Vinkel i grader
Θ = 360 × 18 /2 × π × 10
Θ = 103,13°
Cirklens centrale vinkel er således 103,13°.
Spørgsmål 3: Find vinklen på et parallelogram, hvis de tre andre vinkler er 80°, 95° og 105°?
Løsning :
Der er fire sider i et parallelogram med den samlede sum af vinkler 360°.
Formel til at finde summen af vinkler = 180 (n – 2)
Hvor,
n er antallet af sider af en polygon
Her er n = 4,
Den samlede sum af vinkler = 180 (4 – 2)
= 180 (2)
= 360°
Samlet sum = Vinkel 1 + Vinkel 2 + Vinkel 3 + Vinkel 4
360 = 80+ 95+ 105+ Vinkel 4
360 = 280 + Vinkel 4
Vinkel 4 = 360 – 280
Vinkel 4 = 80°
Spørgsmål 4: Find vinkel A i den givne figur.

Løsning :
Givet: Hypotenuse = 12
Vinkelret = 6
Trigonometrifunktionen til at beregne vinklen er givet ved:
sinA = 6/12
A = 30°
Spørgsmål 5: Find vinkel A i den givne figur.

Løsning :
forskel mellem firma og virksomhed
Givet: Hypotenuse = 10
Base = 5
Trigonometrifunktionen til at beregne vinklen er givet ved:
CosA = 5/10
A = 60°
Spørgsmål 6: Find vinklen på en femkant, hvis andre fire vinkler er 115°, 100°, 105° og 100°?
Løsning :
Der er fem sider i en femkant med den samlede sum af vinkler 540°.
Formel til at finde summen af vinkler = 180 (n – 2)
Hvor,
n er antallet af sider af en polygon
Her er n = 5,
Samlet sum af vinkler = 180 (5 – 2)
= 180 (3)
= 540°
Samlet sum = Vinkel 1 + Vinkel 2 + Vinkel 3 + Vinkel 4 + Vinkel 5
540 = 115° + 100° + 105°+100° + Vinkel 5
540 = 420 + Vinkel 5
Vinkel 5 = 540 – 420
Vinkel 5 = 120°
Spørgsmål 7: Find vinkel A i den givne figur.

Løsning :
Givet: Basis = √3
Vinkelret = 1
Trigonometrifunktionen til at beregne vinklen er givet ved:
tanθ =
tanθ = 1/√3
A = 30°
Spørgsmål 8: Find vinklen på et parallelogram, hvis andre tre vinkler er 100°, 70° og 80°?
Løsning :
Der er fire sider i et parallelogram med den samlede sum af vinkler 360°.
Formel til at finde summen af vinkler = 180 (n – 2)
Hvor,
n er antallet af sider af en polygon
Her er n = 4,
Samlet sum af vinkler = 180 (4 – 2)
= 180 (2)
= 360°
Samlet sum = Vinkel 1 + Vinkel 2 + Vinkel 3 + Vinkel 4
360 = 100 + 70 + 80 + Vinkel 4
360 = 250 + Vinkel 4
Vinkel 4 = 360 – 250
Vinkel 4 = 110°
Den anden vinkel er således 110°.
Spørgsmål 9: Find vinklen på en sekskant, hvis andre fem vinkler er 120°, 115°, 110°, 125° og 105°?
Løsning :
Der er seks sider i en sekskant med den samlede sum af vinkler 720°.
Formel til at finde summen af vinkler = 180 (6 – 2)
Hvor,
n er antallet af sider af en polygon
Her er n = 6,
manuel testSamlet sum af vinkler = 180 (6 – 2)
= 180 (4)
= 720°
Samlet sum = Vinkel 1 + Vinkel 2 + Vinkel 3 + Vinkel 4 + Vinkel 5 + Vinkel 6
720 = 120 + 115 + 110 + 125 + 105 + Vinkel 6
720 = 575 + Vinkel 6
Vinkel 6 = 720 – 575
Vinkel 6 = 145°
Således er den sjette sekskantvinkel 145°.






