Givet to strenge, S1 og S2 , er opgaven at finde længden af ​​den længste fælles sekvens, dvs. den længste sekvens til stede i begge strenge.

deterministiske endelige automater

EN længste fælles subsequence (LCS) er defineret som den længste undersekvens, der er fælles i alle givne inputsekvenser.

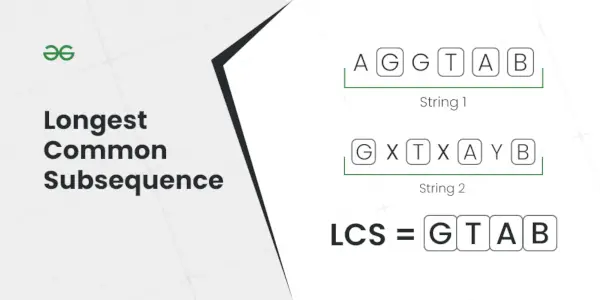
Længste fælles efterfølger

Eksempler:

Input: S1 = ABC, S2 = ACD
Produktion: 2
Forklaring: Den længste undersekvens, der er til stede i begge strenge, er AC.

Input: S1 = AGGTAB, S2 = GXTXAYB
Produktion: 4
Forklaring: Den længste almindelige undersekvens er GTAB.

Input: S1 = ABC, S2 = CBA
Produktion: 1
Forklaring: Der er tre almindelige undersekvenser af længde 1, A, B og C og ingen fælles undersekvens af længde mere end 1.

Input: S1 = XYZW, S2 = XYWZ
Produktion: 3
Forklaring: Der er to almindelige undersekvenser med længde 3 XYZ og XYW, og ingen fælles undersekvens. af længde mere end 3.

Længste fælles subsequence (LCS) ved hjælp af rekursion:

Generer alle mulige undersekvenser og find den længste blandt dem, der er til stede i begge strenge ved hjælp af Følg nedenstående trin for at implementere ideen:

python-program til binær søgning

• Opret en rekursiv funktion [sig lcs() ].
• Tjek forholdet mellem de første tegn i strengene, der endnu ikke er behandlet.
  • Afhængigt af relationen kalder den næste rekursive funktion som nævnt ovenfor.
• Returner længden af ​​det modtagne LCS som svar.

Nedenfor er implementeringen af ​​den rekursive tilgang:

C++

// A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

C

// A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>b) ? a:b; } // Driverkode int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0, j = 0;  // Funktion Kald printf('Længde af LCS er %d', lcs(S1, S2, i, j));  retur 0; }>

Java

// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b) ? a:b; } // Driverkode public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.længde();  int n = S2.længde();  System.out.println('Længde af LCS er' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Denne kode er bidraget af Saket Kumar>

Python

# A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>

C#

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b) ? a:b; } // Driverkode offentlig statisk void Main() { String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.Længde;  int n = S2.Længde;  Console.Write('Længde af LCS er' + ' ' + lcs(S1, S2, m, n));  } } // Denne kode er bidraget af Sam007>

Javascript

>

PHP

 // A Naive recursive PHP  // implementation of LCS problem  function lcs($X, $Y, $m, $n)  $n == 0) return 0; else if ($X[$m - 1] == $Y[$n - 1]) return 1 + lcs($X, $Y, $m - 1, $n - 1); else return max(lcs($X, $Y, $m, $n - 1), lcs($X, $Y, $m - 1, $n));  // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; echo 'Length of LCS is '; echo lcs($S1 , $S2, strlen($S1), strlen($S2)); // This code is contributed  // by Shivi_Aggarwal  ?>>

Produktion

Length of LCS is 4>

Tidskompleksitet: O(2^m+n)
Hjælpeplads: O(1)

Længste fælles subsequence (LCS) ved hjælp af Memoisering :

Hvis vi lægger mærke til det, kan vi observere, at ovenstående rekursive løsning har følgende to egenskaber:

1. Optimal underbygning:

Se for at løse strukturen af ​​L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) vi tager hjælp af understrukturerne af X[0 , 1, …, m-2], Y[0, 1,…, n-2], afhængigt af situationen (dvs. at bruge dem optimalt) for at finde løsningen af ​​helheden.

2. Overlappende underproblemer:

Hvis vi bruger ovenstående rekursive tilgang til strenge BD og ABCD , vil vi få et delvist rekursionstræ som vist nedenfor. Her kan vi se, at delproblemet L(BD, ABCD) bliver beregnet mere end én gang. Hvis det samlede træ betragtes, vil der være flere sådanne overlappende underproblemer.

L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
//
L(AXY, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)

Nærme sig: På grund af tilstedeværelsen af ​​disse to egenskaber kan vi bruge Dynamisk programmering eller Memoization til at løse problemet. Nedenfor er tilgangen til løsningen ved hjælp af rekursion.

• Opret en rekursiv funktion. Opret også et 2D-array for at gemme resultatet af en unik tilstand.
• Under rekursionsopkaldet, hvis den samme tilstand kaldes mere end én gang, kan vi direkte returnere svaret, der er gemt for denne tilstand, i stedet for at beregne igen.

Nedenfor er implementeringen af ​​ovenstående tilgang:

C++

// A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) returner 0;  hvis (X[m - 1] == Y[n - 1]) returner dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Driverkode int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  vektor> dp(m + 1, vektor (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>

Java

/*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>

Python

# A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>

C#

/* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>b) ? a:b; } public static void Main() { String s1 = 'AGGTAB';  String s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X. Længde;  int n = Y. Længde;  int[,] L = ny int[m + 1, n + 1];  for (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>

Javascript

/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>

Produktion

Length of LCS is 4>

Tidskompleksitet: O(m * n) hvor m og n er strenglængderne.
Hjælpeplads: O(m * n) Her ignoreres det rekursive stakrum.

Længste almindelige delsekvens (LCS) ved brug af bottom-up (tabel):

Vi kan bruge følgende trin til at implementere den dynamiske programmeringstilgang til LCS.

binært træ vs binært søgetræ

• Opret et 2D-array dp[][] med rækker og kolonner lig med længden af ​​hver inputstreng plus 1 [antallet af rækker angiver indeksene for S1 og kolonnerne angiver indeksene for S2 ].
• Initialiser den første række og kolonne i dp-arrayet til 0.
• Iterer gennem rækkerne i dp-arrayet, startende fra 1 (f.eks. brug iterator jeg ).
  • For hver jeg , gentag alle kolonnerne fra j = 1 til n :
    • Hvis S1[i-1] er lig med S2[j-1] , indstil det aktuelle element i dp-arrayet til værdien af ​​elementet til ( dp[i-1][j-1] + 1 ).
    • Ellers skal du indstille det aktuelle element i dp-arrayet til den maksimale værdi af dp[i-1][j] og dp[i][j-1] .
• Efter de indlejrede sløjfer vil det sidste element i dp-arrayet indeholde længden af ​​LCS.

Se nedenstående illustration for en bedre forståelse:

Illustration:

Sig, at strengene er S1 = AGGTAB og S2 = GXTXAYB .

Første skridt: Opret først en 2D-matrix (f.eks. dp[][]) i størrelsen 8 x 7, hvis første række og første kolonne er fyldt med 0.

Oprettelse af dp-tabellen

Andet trin: Travers for i = 1. Når j bliver 5, er S1[0] og S2[4] lige store. Så dp[][] er opdateret. For de andre elementer tag maksimum af dp[i-1][j] og dp[i][j-1]. (I dette tilfælde, hvis begge værdier er ens, har vi brugt pile til de foregående rækker).

Udfyldning af række nr. 1

lytteport

Tredje trin: Mens krydset for i = 2, er S1[1] og S2[0] de samme (begge er 'G'). Så dp-værdien i den celle opdateres. Resten af ​​elementerne opdateres i henhold til betingelserne.

Udfyldning af rækkenr. 2

Fjerde trin: For i = 3 er S1[2] og S2[0] igen ens. Opdateringerne er som følger.

Fyldningsrækkenr. 3

Femte trin: For i = 4 kan vi se, at S1[3] og S2[2] er ens. Så dp[4][3] opdateret som dp[3][2] + 1 = 2.

Fyldningsrække 4

Sjette trin: Her kan vi se, at for i = 5 og j = 5 er værdierne af S1[4] og S2[4] de samme (dvs. begge er 'A'). Så dp[5][5] opdateres i overensstemmelse hermed og bliver 3.

Fyldningsrække 5

Sidste trin: For i = 6, se de sidste tegn i begge strenge er ens (de er 'B'). Derfor bliver værdien af ​​dp[6][7] 4.

Fylder den sidste række

Så vi får den maksimale længde af fælles efterfølger som 4 .

java compareto metode

Følgende er en tabel for implementering af LCS-problemet.

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>

Java

// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>b) ? a:b; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.længde();  int n = S2.længde();  System.out.println('Længde af LCS er' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Denne kode er bidraget af Saket Kumar>

Python

# Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>b) ? a:b; } // Driverkode offentlig statisk void Main() { String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  int m = S1.Længde;  int n = S2.Længde;  Console.Write('Længde af LCS er' + ' ' + lcs(S1, S2, m, n));  } } // Denne kode er bidraget af Sam007>

Javascript

// Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers  function max(a, b) {  if (a>b) returnere a;  ellers returnere b; } // Returnerer længden af ​​LCS for X[0..m-1], Y[0..n-1] funktion lcs(X, Y, m, n) { var L = new Array(m + 1);  for(var i = 0; i< L.length; i++)   {  L[i] = new Array(n + 1);  }  var i, j;    /* Following steps build L[m+1][n+1] in  bottom up fashion. Note that L[i][j]  contains length of LCS of X[0..i-1]  and Y[0..j-1] */  for(i = 0; i <= m; i++)  {  for(j = 0; j <= n; j++)   j == 0)  L[i][j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }    /* L[m][n] contains length of LCS  for X[0..n-1] and Y[0..m-1] */  return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>

PHP

 // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>

Produktion

Length of LCS is 4>

Tidskompleksitet: O(m * n), hvilket er meget bedre end den værst tænkelige tidskompleksitet ved naiv rekursiv implementering.
Hjælpeplads: O(m * n), fordi algoritmen bruger en matrix af størrelse (m+1)*(n+1) til at gemme længden af ​​de fælles understrenge.

Længste fælles subsequence (LCS) ved hjælp af Bottom-Up (space-optimering):

• I ovenstående tabuleringstilgang bruger vi L[i-1][j] og L[i][j] osv., her refererer L[i-1] testamentet til matricen L's forrige række og L[i] refererer til den aktuelle række.
• Vi kan lave rumoptimering ved at bruge to vektorer, en er tidligere og en anden er aktuel.
• Når den indre for sløjfe forlader vi initialiserer forrige lig med nuværende.

Nedenfor er implementeringen:

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector forrige(m + 1, 0), cur(m + 1, 0);  for (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>

Java

// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>

Python

def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>

C#

using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>

Javascript

function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>

Produktion

Length of LCS is 4>

Tidskompleksitet: O(m * n), som forbliver den samme.
Hjælpeplads: O(m), fordi algoritmen bruger to arrays af størrelsen m.