- DFA refererer til deterministiske endelige automater. Deterministisk refererer til det unikke ved beregningen. De endelige automater kaldes deterministiske endelige automater, hvis maskinen læses en inputstreng et symbol ad gangen.
- I DFA er der kun én vej til specifik input fra den aktuelle tilstand til den næste tilstand.
- DFA accepterer ikke nul-bevægelsen, dvs. DFA'en kan ikke ændre tilstand uden noget inputtegn.
- DFA kan indeholde flere endelige tilstande. Det bruges i leksikalsk analyse i compiler.
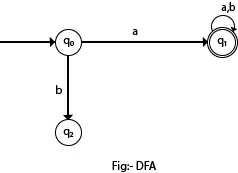
I det følgende diagram kan vi se, at fra tilstand q0 for input a, er der kun én vej, som går til q1. På samme måde er der fra q0 kun én vej for input b, der går til q2.
Formel definition af DFA
En DFA er en samling af 5-tupler, som vi har beskrevet i definitionen af FA.
java arv
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Overgangsfunktion kan defineres som:
δ: Q x ∑→Q
Grafisk repræsentation af DFA
En DFA kan repræsenteres af digrafer kaldet tilstandsdiagram. Hvori:
- Staten er repræsenteret ved toppunkter.
- Buen mærket med et inputtegn viser overgangene.
- Starttilstanden er markeret med en pil.
- Den endelige tilstand er angivet med en dobbelt cirkel.
Eksempel 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Løsning:
Overgangsdiagram:

Overgangstabel:
| Nuværende tilstand | Næste tilstand for input 0 | Næste inputtilstand 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Eksempel 2:
DFA med ∑ = {0, 1} accepterer alle, der starter med 0.
Løsning:

Forklaring:
print fra java
- I ovenstående diagram kan vi se, at på givet 0 som input til DFA i tilstand q0 ændrer DFA tilstand til q1 og går altid til sluttilstand q1 ved start af input 0. Den kan acceptere 00, 01, 000, 001... .etc. Den kan ikke acceptere en streng, der starter med 1, fordi den aldrig vil gå til den endelige tilstand på en streng, der starter med 1.
Eksempel 3:
DFA med ∑ = {0, 1} accepterer alle, der ender med 0.
Løsning:

Forklaring:
I ovenstående diagram kan vi se, at på givet 0 som input til DFA i tilstand q0, ændrer DFA tilstand til q1. Det kan acceptere enhver streng, der ender med 0 som 00, 10, 110, 100 ... osv. Den kan ikke acceptere en streng, der slutter med 1, fordi den aldrig vil gå til den endelige tilstand q1 på 1 input, så strengen, der slutter med 1, vil ikke blive accepteret eller vil blive afvist.
