Begrebet Memoisering kommer af det latinske ord notat ( at huske ), som almindeligvis forkortes til memo på amerikansk engelsk, og som betyder at transformere resultaterne af en funktion til noget at huske.
Inden for databehandling bruges memoization til at fremskynde computerprogrammer ved at eliminere den gentagne beregning af resultater og ved at undgå gentagne opkald til funktioner, der behandler det samme input.

Hvad er huskeseddel
Indholdsfortegnelse
- Hvad er Memoization?
- Hvorfor bruges Memoization>
- Hvor kan man bruge Memoization?
- Typer af Memoization
- Hvordan memoiseringsteknik bruges i dynamisk programmering?
- Hvordan Memoization er forskellig fra tabulering?
- Problemer med kodningspraksis til huskeseddel
- Ofte stillede spørgsmål
- 1) Er memoization bedre end DP?
- 2) Er memoization det samme som caching?
- 3) Hvorfor huskes det top-down?
- 4) Bruger memoization rekursion?
- 5) Skal jeg bruge tabulering eller huskeseddel?
- 6) Hvor bruges huskeseddel?
- 7) Hvorfor kaldes det memorisering?
- 8) Hvordan reducerer memorisering tidskompleksitet?
- 9) Hvad er forskellen mellem memoization og caching?
- 10) Hvorfor er tabulering hurtigere end huskeskrivning?
- Konklusion
Hvorfor bruges Memoization?
Memoisering er en bestemt form for caching der bruges i dynamisk programmering . Formålet med caching er at forbedre ydeevnen af vores programmer og holde data tilgængelige, som kan bruges senere. Den gemmer grundlæggende det tidligere beregnede resultat af delproblemet og bruger det lagrede resultat til det samme delproblem. Dette fjerner den ekstra indsats for at beregne igen og igen for det samme problem. Og vi ved allerede, at hvis det samme problem opstår igen og igen, så er det problem af rekursiv karakter.
Hvor kan man bruge Memoization?
Vi kan bruge husketeknikken, hvor brug af de tidligere beregnede resultater kommer ind i billedet. Denne form for problemer bruges mest i forbindelse med rekursion , især med problemer, der involverer overlappende delproblemer .
Lad os tage et eksempel, hvor det samme underproblem gentages igen og igen.
Eksempel til at vise, hvor man kan bruge huskeseddel:
Let us try to find the factorial of a number .>
Nedenfor er en rekursiv metode for at finde fakultetet af et tal:
int factorial(usigneret int n)
{
hvis (n == 0)
retur 1;
returner n * factorial(n – 1);
}
Hvad sker der, hvis vi bruger denne rekursive metode?
Hvis du skriver den komplette kode til ovenstående kodestykke, vil du bemærke, at der vil være 2 metoder i koden:
1. factorial(n) 2. main()>
Hvis vi nu har flere forespørgsler for at finde faktorialet, såsom at finde factorial af 2, 3, 9 og 5, så bliver vi nødt til at kalde factorial()-metoden 4 gange:
factorial(2) factorial(3) factorial(9) factorial(5)>
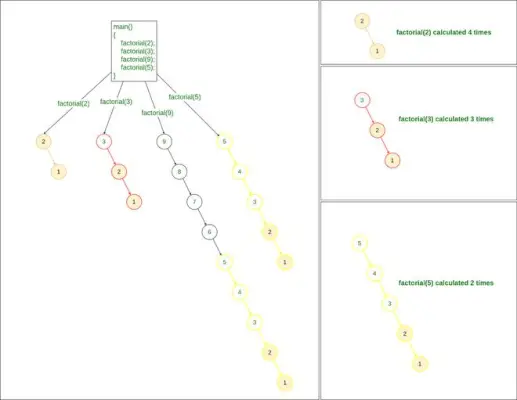
Rekursiv metode til at finde Faktoriel
Så det er sikkert at sige, at for at finde fakultet af tal K-tal, vil den nødvendige tidskompleksitet være O(N*K)
- PÅ) at finde fakultetet for et bestemt tal, og
- PIL) at kalde factorial() metoden K forskellige tidspunkter.
Hvordan Memoization kan hjælpe med sådanne problemer?
Hvis vi bemærker i ovenstående problem, mens beregningsfaktoren på 9:
c#
- Vi beregner fakultetet af 2
- Vi beregner også faktoren af 3,
- og vi beregner også faktoren 5
Derfor, hvis vi gemmer resultatet af hver enkelt faktor på det første tidspunkt for beregningen, kan vi nemt returnere fakultetet for ethvert påkrævet tal på kun O(1) tid. Denne proces er kendt som Memoisering .
Løsning ved hjælp af Memoization (Hvordan fungerer Memoization?):
Hvis vi først finder factorialet på 9 og gemmer resultaterne af individuelle delproblemer, kan vi nemt udskrive factorialet for hvert input i O(1).
Derfor vil tidskompleksiteten til at finde faktornumre ved hjælp af huskes være PÅ)
- PÅ) for at finde faktoren for det største input
- O(1) for at udskrive fakultetet for hvert input.
Typer af Memoization
Implementeringen af memoization afhænger af de skiftende parametre, der er ansvarlige for at løse problemet. Der er forskellige dimensioner af caching, der bruges i memoiseringsteknik. Nedenfor er nogle af dem:
- 1D Memoization: Den rekursive funktion, der kun har ét argument, hvis værdi ikke var konstant efter hvert funktionskald.
- 2D Memoization: Den rekursive funktion, der kun har to argumenter, hvis værdi ikke var konstant efter hvert funktionskald.
- 3D Memoization : Den rekursive funktion, der kun har tre argumenter, hvis værdier ikke var konstante efter hvert funktionskald.
Hvordan Memoization teknik bruges i dynamisk programmering?
Dynamisk programmering hjælper til effektivt at løse problemer, der har overlappende delproblemer og optimale understrukturegenskaber. Ideen bag dynamisk programmering er at dele problemet op i mindre delproblemer og gemme resultatet til fremtidig brug, og dermed eliminere behovet for at beregne resultatet gentagne gange.
Der er to tilgange til at formulere en dynamisk programmeringsløsning:
- Top-down tilgang: Denne tilgang følger huskes teknik . Den består af rekursion og caching . Ved beregning repræsenterer rekursion processen med at kalde funktioner gentagne gange, hvorimod cache refererer til processen med at gemme mellemresultater.
- Bottom-up tilgang: Denne tilgang bruger tabulering teknik at implementere den dynamiske programmeringsløsning. Den løser de samme problemer som før, men uden gentagelser. I denne tilgang erstatter iteration rekursion. Derfor er der ingen stak overløbsfejl eller overhead af rekursive procedurer.
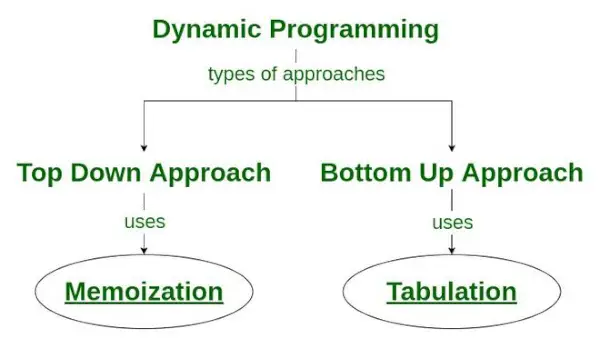
Hvordan Memoization teknik bruges i dynamisk programmering
Hvordan Memoization er forskellig fra tabulering?

Tabulation vs Memoization
For flere detaljer henvises til: Tabulation vs. Memoisering
Problemer med kodningspraksis på huskeseddel
| Spørgsmål | Artikel | Øve sig | Video |
|---|---|---|---|
| Tæl måder at nå den n’te trappe på | Udsigt | Løse | Holde øje |
| Word Break Problem | DP-32 | Udsigt | Løse | Holde øje |
| Program til Fibonacci-numre | Udsigt | Løse | Holde øje |
| n. catalansk nummer | Udsigt | Løse | Holde øje |
| Guldmine problem | Udsigt | Løse | Holde øje |
| Subset Sum Problem | Udsigt | Løse | Holde øje |
| Skæring af en stang | Udsigt | Løse | Holde øje |
| Min omkostningssti | Udsigt | Løse | Holde øje |
| Minimum antal hop for at nå slutningen | Udsigt | Løse | Holde øje |
| Længste palindromiske understreng | Sæt 1 | Udsigt | Løse | Holde øje |
| Længste gentagelsessekvens | Udsigt | Løse | Holde øje |
| Tæl måder at nå den n'te trappe ved at bruge trin 1, 2 eller 3 | Udsigt | Løse | Holde øje |
| Optælling af forskellige måder at udtrykke N på som summen af 1, 3 og 4 es5 vs es6 | Udsigt | Løse | Holde øje |
| Tæl antallet af måder at tilbagelægge en afstand på | Udsigt | Løse | Holde øje |
| Antal arrays med på hinanden følgende element med forskellige værdier | Udsigt | Løse | Holde øje |
| Største Sum Contiguous Subarray | Udsigt | Løse | Holde øje |
| Mindste sum sammenhængende underarray | Udsigt | Løse | Holde øje |
| Unikke stier i et gitter med forhindringer | Udsigt | Løse | Holde øje |
| Forskellige måder at summere n på ved hjælp af tal større end eller lig med m | Udsigt | Løse | Holde øje |
Ofte stillede spørgsmål (FAQs) om Memoization
1: Er memoization bedre end DP?
Memoization er top-down-tilgangen til at løse et problem med dynamisk programmering. Det kaldes memoisering, fordi vi vil oprette et notat for de værdier, der returneres fra at løse hvert problem.
2: Er memoisering det samme som caching?
Memoisering er faktisk en bestemt type caching. Udtrykket caching kan generelt henvise til enhver lagringsteknik (såsom HTTP caching) til fremtidig brug, men memoizing refererer mere specifikt til cachingfunktion, der returnerer værdien.
3: Hvorfor huskes der top-down?
Top-Down-tilgangen deler det store problem op i flere underproblemer. hvis underproblemet allerede er løst, så genbrug svaret. Ellers skal du løse underproblemet og gemme resultatet i noget hukommelse.
4: Bruger memoization rekursion?
Memoisering følger top-down tilgang til at løse problemet. Den består af rekursion og caching. Ved beregning repræsenterer rekursion processen med at kalde funktioner gentagne gange, hvorimod cache refererer til processen med at gemme mellemresultater.
5: Skal jeg bruge tabulering eller huskeseddel?
For problemer, der kræver, at alle delproblemer skal løses, udkonkurrerer tabulering typisk memoisering med en konstant faktor. Dette skyldes, at tabuleringen ikke har nogen overhead af rekursion, hvilket reducerer tiden til at løse rekursionsopkaldsstakken fra stakhukommelsen.
Når et delproblem skal løses for at det oprindelige problem kan løses, er huskeseddel at foretrække, da et delproblem løses dovent, dvs. kun de beregninger, der kræves, udføres.
6: Hvor bruges huskeseddel?
Memoisering er en optimeringsteknik, der bruges til at fremskynde computerprogrammer ved at cache resultaterne af dyre funktionskald og returnere dem, når de samme input støder på igen.
7: Hvorfor kaldes det memorisering?
Udtrykket memoization kommer fra det latinske ord memorandum (at huske), som almindeligvis forkortes til memo på amerikansk engelsk, og som betyder at transformere resultaterne af en funktion til noget at huske.
8: Hvordan reducerer memorisering tidskompleksitet?
At løse det samme problem igen og igen tager tid og øger kørselstidskompleksiteten af det overordnede program. Dette problem kan løses ved at opretholde en cache eller hukommelse, hvor vi gemmer det allerede beregnede resultat af problemet for et bestemt input. Så hvis vi ikke vil genberegne det samme problem, kan vi blot bruge resultatet, der er gemt i hukommelsen og reducere tidskompleksiteten.
9: Hvad er forskellen mellem memoization og caching?
Memoisering er faktisk en specifik type caching, der involverer cachelagring af returværdien af en funktion baseret på input. Caching er en mere generel betegnelse. For eksempel er HTTP-caching caching, men det er ikke memoisering.
10: Hvorfor er tabulering hurtigere end huskeskrivning?
Tabulation er normalt hurtigere end memoisering, fordi den er iterativ, og løsning af underproblemer kræver ingen overhead af rekursive opkald.
Memoisering er en teknik, der bruges inden for datalogi til at fremskynde udførelsen af rekursive eller beregningsmæssigt dyre funktioner ved at cache resultaterne af funktionskald og returnere de cachelagrede resultater, når de samme input forekommer igen.
Den grundlæggende idé med memoization er at gemme outputtet af en funktion for et givet sæt af input og returnere det cachelagrede resultat, hvis funktionen kaldes igen med de samme input. Denne teknik kan spare beregningstid, især for funktioner, der kaldes ofte eller har en høj tidskompleksitet.
Her er en trin-for-trin guide til implementering af memoization:
Identificer den funktion, du ønsker at optimere ved hjælp af huskeseddel. Denne funktion skal have gentagne og dyre beregninger for det samme input.
Opret et ordbogsobjekt for at gemme de cachelagrede resultater af funktionen. Nøglerne til ordbogen skal være inputparametrene til funktionen, og værdierne skal være de beregnede resultater.
I begyndelsen af funktionen skal du kontrollere, om inputparametrene allerede er til stede i cacheordbogen. Hvis de er, returner det cachelagrede resultat.
Hvis inputparametrene ikke er i cacheordbogen, skal du beregne resultatet og gemme det i cacheordbogen med inputparametrene som nøglen.
Returner det beregnede resultat.
Her er et Python-kodeeksempel på implementering af memoization ved hjælp af en ordbog:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
>Produktion
>
I ovenstående kode definerer vi en funktion kaldet fibonacci, der beregner det n'te tal i Fibonacci-sekvensen. Vi bruger et ordbogsobjekt kaldet cache til at gemme resultaterne af funktionskaldene. Hvis inputparameteren n allerede er til stede i cacheordbogen, returnerer vi det cachelagrede resultat. Ellers beregner vi resultatet ved hjælp af rekursive kald til fibonacci-funktionen og gemmer det i cache-ordbogen, før vi returnerer det.
Memoisering kan bruges til at optimere ydeevnen af mange funktioner, der har gentagne og dyre beregninger. Ved at cache resultaterne af funktionskald kan vi undgå unødvendige beregninger og fremskynde udførelsen af funktionen.
Konklusion
Memoization er et programmeringskoncept og kan anvendes på ethvert programmeringssprog. Dets absolutte mål er at optimere programmet. Normalt ses dette problem, når programmer udfører tunge beregninger. Denne teknik cacherer alle de tidligere resultater, der er beregnet, så det ikke skal genberegnes for det samme problem.
Relaterede artikler:
- Memoisering ved hjælp af dekoratorer i Python
- JavaScript Memoization
