logo

TechCodeview

Største tal i BST, som er mindre end eller lig med k

Givet roden til en Binært søgetræ og et heltal k . Opgaven er at finde største antal i det binære søgetræ altså mindre end eller lige til k hvis der ikke findes et sådant element print -1. 

Eksempler:  

Input:



Største-antal-i-BST-som-er-mindre-end-eller-lig-til-k-1' title=

Output: 21
Forklaring: 19 og 25 er de to tal, der er tættest på 21, og 19 er det største tal med værdi mindre end eller lig med 21.

Input: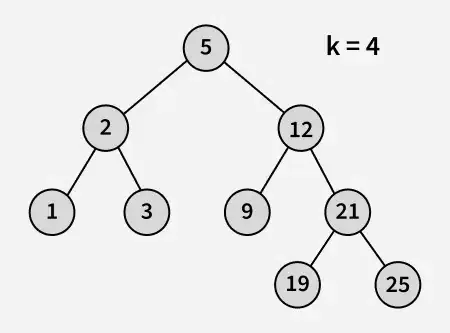

Største-antal-i-BST-som-er-mindre-end-eller-lig-til-k-2' loading='lazy' title=

Output: 3
Forklaring: 3 & 5 er de to tal, der er tættest på 4, og 3 er det største tal med værdi mindre end eller lig med 4.

Indholdsfortegnelse

[Naiv tilgang] Brug af rekursion - O(h) tid og O(h) rum

Tanken er at starte kl rod og sammenlign dens værdi med k. Hvis nodens værdi er større end k, flyttes til venstre undertræ. Ellers find værdien af ​​største tal mindre end lig med k i højre undertræ . Hvis højre undertræ returnerer -1 (hvilket betyder, at der ikke findes en sådan værdi), så returner den aktuelle nodes værdi. Ellers returnerer værdien returneret af højre undertræ (da den vil være større end den nuværende nodes værdi, men mindre end lig med k).

C++ 
// C++ code to find the largest value  // smaller than or equal to k using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;    Node(int val){  data = val;  left = nullptr;  right = nullptr;  } }; // function to find max value less than k int findMaxFork(Node* root int k) {    // Base cases  if (root == nullptr)  return -1;  if (root->data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root->data < k) {    int x = findMaxFork(root->right k);  if (x == -1)  return root->data;  else  return x;  }  // If root's data is greater   // return value from left subtree.  return findMaxFork(root->left k);  } int main() {    int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node* root = new Node(5);  root->left = new Node(2);  root->left->left = new Node(1);  root->left->right = new Node(3);  root->right = new Node(12);  root->right->left = new Node(9);  root->right->right = new Node(21);  root->right->right->left = new Node(19);  root->right->right->right = new Node(25);    cout << findMaxFork(root k);  return 0; }
Java 
// Java code to find the largest value  // smaller than or equal to k using recursion class Node {  int data;  Node left right;    Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int findMaxFork(Node root int k) {    // Base cases  if (root == null)  return -1;  if (root.data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  int x = findMaxFork(root.right k);  if (x == -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return findMaxFork(root.left k);  }  public static void main(String[] args) {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  System.out.println(findMaxFork(root k));  } }
Python 
# Python code to find the largest value  # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): # Base cases if root is None: return -1 if root.data == k: return k # If root's value is smaller # try in right subtree elif root.data < k: x = findMaxFork(root.right k) if x == -1: return root.data else: return x # If root's data is greater # return value from left subtree. return findMaxFork(root.left k) if __name__ == '__main__': k = 24 # creating following BST # # 5 # /   # 2 12 # /  /   # 1 3 9 21 # /   # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
C# 
// C# code to find the largest value  // smaller than or equal to k using recursion using System; class Node {  public int data;  public Node left right;    public Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int FindMaxFork(Node root int k) {    // Base cases  if (root == null)  return -1;  if (root.data == k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  int x = FindMaxFork(root.right k);  if (x == -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return FindMaxFork(root.left k);  }  static void Main() {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  Console.WriteLine(FindMaxFork(root k));  } }
JavaScript 
// JavaScript code to find the largest value  // smaller than or equal to k using recursion class Node {  constructor(val) {  this.data = val;  this.left = null;  this.right = null;  } } // function to find max value less than k function findMaxFork(root k) {    // Base cases  if (root === null)  return -1;  if (root.data === k)  return k;  // If root's value is smaller  // try in right subtree  else if (root.data < k) {  let x = findMaxFork(root.right k);  if (x === -1)  return root.data;  else  return x;  }  // If root's data is greater  // return value from left subtree.  return findMaxFork(root.left k); } let k = 24; // creating following BST // // 5 // /   // 2 12 // /  /   // 1 3 9 21 // /   // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));

Produktion 
21

[Forventet tilgang] Brug af iteration - O(h) tid og O(1) mellemrum

Tanken er at starte kl rod og sammenligne dens værdi med k . Hvis nodens værdi er <= k opdater resultatværdien til roots værdi og flyt til højre undertræ ellers flytte til venstre undertræ. Ved iterativt Ved at anvende denne operation på tværs af alle noder kan vi minimere den nødvendige plads til rekursion stak.

C++ 
// C++ code to find the largest value  // smaller than or equal to k using recursion #include    using namespace std; class Node { public:  int data;  Node *left *right;    Node(int val){  data = val;  left = nullptr;  right = nullptr;  } }; // function to find max value less than k int findMaxFork(Node* root int k) {    int result = -1;    // Start from root and keep looking for larger   while (root != nullptr) {  // If root is smaller go to right side  if (root->data <= k){  result = root->data;  root = root->right;  }  // If root is greater go to left side   else  root = root->left;  }    return result; } int main() {    int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node* root = new Node(5);  root->left = new Node(2);  root->left->left = new Node(1);  root->left->right = new Node(3);  root->right = new Node(12);  root->right->left = new Node(9);  root->right->right = new Node(21);  root->right->right->left = new Node(19);  root->right->right->right = new Node(25);    cout << findMaxFork(root k);  return 0; }
Java 
// Java code to find the largest value  // smaller than or equal to k using recursion class Node {  int data;  Node left right;    Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int findMaxFork(Node root int k) {  int result = -1;    // Start from root and keep looking for larger   while (root != null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result;  }  public static void main(String[] args) {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  System.out.println(findMaxFork(root k));  } }
Python 
# Python code to find the largest value  # smaller than or equal to k using recursion class Node: def __init__(self val): self.data = val self.left = None self.right = None # function to find max value less than k def findMaxFork(root k): result = -1 # Start from root and keep looking for larger  while root is not None: # If root is smaller go to right side if root.data <= k: result = root.data root = root.right # If root is greater go to left side  else: root = root.left return result if __name__ == '__main__': k = 24 # creating following BST # # 5 # /   # 2 12 # /  /   # 1 3 9 21 # /   # 19 25 root = Node(5) root.left = Node(2) root.left.left = Node(1) root.left.right = Node(3) root.right = Node(12) root.right.left = Node(9) root.right.right = Node(21) root.right.right.left = Node(19) root.right.right.right = Node(25) print(findMaxFork(root k))
C# 
// C# code to find the largest value  // smaller than or equal to k using recursion using System; class Node {  public int data;  public Node left right;    public Node(int val) {  data = val;  left = null;  right = null;  } } class GfG {    // function to find max value less than k  static int FindMaxFork(Node root int k) {  int result = -1;    // Start from root and keep looking for larger   while (root != null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result;  }  static void Main() {  int k = 24;  // creating following BST  //  // 5  // /    // 2 12  // /  /    // 1 3 9 21  // /    // 19 25  Node root = new Node(5);  root.left = new Node(2);  root.left.left = new Node(1);  root.left.right = new Node(3);  root.right = new Node(12);  root.right.left = new Node(9);  root.right.right = new Node(21);  root.right.right.left = new Node(19);  root.right.right.right = new Node(25);  Console.WriteLine(FindMaxFork(root k));  } }
JavaScript 
// JavaScript code to find the largest value  // smaller than or equal to k using recursion class Node {  constructor(val) {  this.data = val;  this.left = null;  this.right = null;  } } // function to find max value less than k function findMaxFork(root k) {  let result = -1;    // Start from root and keep looking for larger   while (root !== null) {  // If root is smaller go to right side  if (root.data <= k) {  result = root.data;  root = root.right;  }  // If root is greater go to left side   else {  root = root.left;  }  }    return result; } let k = 24; // creating following BST // // 5 // /   // 2 12 // /  /   // 1 3 9 21 // /   // 19 25 let root = new Node(5); root.left = new Node(2); root.left.left = new Node(1); root.left.right = new Node(3); root.right = new Node(12); root.right.left = new Node(9); root.right.right = new Node(21); root.right.right.left = new Node(19); root.right.right.right = new Node(25); console.log(findMaxFork(root k));

Produktion 
21
Opret Quiz