Trigonometri er en vigtig gren af matematikken, der beskæftiger sig med forholdet mellem vinkler og længder af siderne i en retvinklet trekant. De seks trigonometriske forhold eller funktioner er sinus, cosinus, tangent, cosecant og sekant, og et trigonometrisk forhold er et forhold mellem siderne i en retvinklet trekant. Sinus-, cosinus- og tangensfunktioner er tre vigtige trigonometriske funktioner, da de tre andre, dvs. cosecant-, sekant- og cotangensfunktioner er de reciproke funktioner af henholdsvis sinus-, cosinus- og tangentfunktioner.
- sin θ = Modsat side/hypotenuse
- cos θ = Tilstødende side/Hypotenuse
- tan θ = Modsat side/tilstødende side
- cosec θ = Hypotenuse/Modsat side
- sek θ = Hypotenuse/tilstødende side
- barneseng θ = Tilstødende side/Modsatte side
Tangentfunktion er en af de 6 trigonometriske funktioner, der bruges i trigonometriske formler .
Indholdsfortegnelse
Tangent formel
Tangent af en vinkel i en retvinklet trekant er forholdet mellem længden af den modsatte side og længden af den tilstødende side til den givne vinkel. Vi skriver en tangentfunktion som tan. Lad os betragte en retvinklet trekant XYZ, og en af dens spidse vinkler er θ. En modsat side er den side, der er modsat vinklen θ, og den tilstødende side er den side, der støder op til vinklen θ.
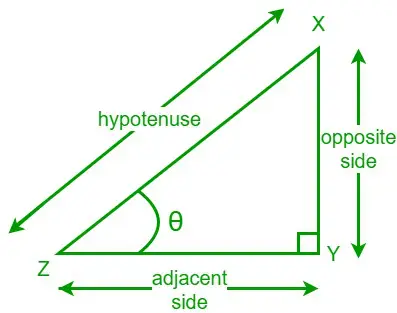
Nu er tangentformlen for den givne vinkel θ,
tan θ = Modsat side/tilstødende side
Nogle grundlæggende Tangent-formler
Tangentfunktion i kvadranter
Tangentfunktionen er positiv i første og tredje kvadrant og negativ i anden og fjerde kvadrant.
- tan (2π + θ) = tan θ (1stkvadrant)
- tan (π – θ) = – tan θ (2ndkvadrant)
- tan (π + θ) = tan θ (3rdkvadrant)
- tan (2π – θ) = – tan θ (4thkvadrant)
Tangentfunktion som en negativ funktion
Tangentfunktionen er en negativ funktion, da tangenten af en negativ vinkel er den negative af en tangent positiv vinkel.
tan (-θ) = – tan θ
Tangentfunktion i form af sinus- og cosinusfunktion
Tangentfunktion i form af sinus- og cosinusfunktioner kan skrives som,
tan θ = sin θ/cos θ
Vi ved, at tan θ = Modsat side/tilstødende side
Divider nu både tælleren og nævneren med hypotenusen
tan θ = (modsat side/hypotenuse)/(tilstødende side/hypotenuse)
Vi ved, at sin θ = modsatte side/hypotenuse
cos θ = tilstødende side/hypotenuse
Derfor er tan θ = sin θ/cos θ
Tangentfunktion i form af sinusfunktion
Tangentfunktion i form af sinusfunktionen kan skrives som,
tan θ = sin θ/(√1 – sin 2 jeg)
Vi ved det,
tan θ = sin θ/cos θ
kø og prioritetskø i java
Fra de pythagoræiske identiteter har vi,
uden2θ + cos2θ = 1
cos2θ = 1 – sin2jeg
cos θ = √(1 – sin2jeg)
Derfor er tan θ = sin θ/(√1 – sin2jeg)
Tangentfunktion i form af cosinusfunktion
Tangentfunktion i form af cosinusfunktionen kan skrives som,
tan θ = (√1 -cos 2 i)/cos i
Vi ved det,
tan θ = sin θ/cos θ
Fra de pythagoræiske identiteter har vi,
uden2θ + cos2θ = 1
uden2θ = 1 – cos2jeg
sin θ = √(1 – cos2jeg)
Derfor er tan θ = (√1 – cos2i)/cos i
Tangent-funktion i form af Cotangent-funktion
Tangentfunktion med hensyn til cotangensfunktionen kan skrives som,
tan θ = 1/seng θ
eller
tan θ = tremmeseng (90° – θ) (eller) tremmeseng (π/2 – θ)
Tangent-funktion i form af Cosecant-funktion
Tangentfunktion i form af cosecant-funktionen kan skrives som,
tan θ = 1/√(cosec 2 i – 1)
Fra de pythagoræiske identiteter har vi,
cosec2θ – barneseng2θ = 1
barneseng2θ = cosec2i – 1
barneseng θ = √(kossek2i – 1)
Vi ved det,
tan θ = 1/seng θ
Derfor er tan θ = 1/√(cosec2i – 1)
Tangentfunktion i form af sekantfunktion
Tangentfunktion med hensyn til sekantfunktionen kan skrives som,
tan θ = √sek 2 i – 1
Fra de pythagoræiske identiteter har vi,
sek2θ – altså2θ = 1
tan θ = sek2i – 1
Derfor er tan θ = √(sek2i – 1)
Tangent funktion i form af dobbelt vinkel
Tangentfunktion for en dobbelt vinkel er,
tan 2θ = (2 tan θ)/(1 – tan 2 jeg)
Tangentfunktion i form af tredobbelt vinkel
Tangentfunktion for en tredobbelt vinkel er,
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 tan 2 jeg)
Tangentfunktion i form af halvvinkel
Tangentfunktion for en halv vinkel er,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Tangentfunktion i form af addition og subtraktion af to vinkler
Sum- og differensformler for en tangentfunktion er,
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Trigonometrisk forholdstabel
| Vinkel (i grader) | Vinkel (i radianer) | synd i | cos θ | tan θ = sin θ/cos θ | cosec θ | sek θ | barneseng i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Udefineret | 1 | Udefineret |
| 30° | s/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | s/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | s/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 formatere en dato i java | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = udefineret | 1 | Udefineret | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Udefineret | -1 | Udefineret |
Løst eksempel på Tangent-formler
Eksempel 1: Find værdien af tan θ hvis sin θ = 2/5 og θ er den første kvadrantvinkel.
Løsning:
givet,
- sin θ = 2/5
Fra de pythagoræiske identiteter, vi har,
uden2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Da θ er den første kvadrantvinkel, er cos θ positiv.
cos θ = √21/5
Vi ved det,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21/21
Så værdien af tan θ når sin θ = 2/5 og θ er i første kvadrant er (2√21) /(21)
Eksempel 2: Find værdien af tan x hvis sek x = 13/12 og x er den fjerde kvadrantvinkel.
Løsning:
Givet, sek x = 13/12
Fra de pythagoræiske identiteter har vi,
sek2x – altså2x = 1
så2x = sek2x – 1= (13/12)2- 1
så2x = (169/144) – 1 = 25/144
tan x = ± 5/12
Da x er den fjerde kvadrantvinkel, er tan x negativ.
tan x = – 5/12
Derfor, tan x = – 5/12
Eksempel 3: Hvis tan X = 2/3 og tan Y = 1/2, hvad er så værdien af tan (X + Y)?
Løsning:
givet,
tan X = 2/3 og tan Y = 1/2
Vi ved det,
tan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Derfor, tan(X + Y) = 7/4
Eksempel 4: Beregn tangentfunktionen, hvis de tilstødende og modstående sider af en retvinklet trekant er henholdsvis 4 cm og 7 cm.
Løsning:
konverter strengdato
givet,
Tilstødende side = 4 cm
Modsatte side = 7 cm
Vi ved det,
tan θ = Modsat side/tilstødende side
tan 6 = 7/4 = 1,75
Derfor, tan θ = 1,75
Eksempel 5: En mand ser på et klokketårn i en vinkel på 60° til toppen af tårnet, hvis højde er 100 m. Hvad er afstanden mellem manden og foden af tårnet?
Løsning:
givet,
Tårnets højde = 100 m og θ = 60°
Lad afstanden mellem mennesket og foden af tårnet = d
Vi har,
tan θ = Modsat side/tilstødende side
brun 60° = 100/d
√3 = 100/d [Siden, så 60° = √3]
d = 100/√3
Derfor er afstanden mellem manden og foden af tårnet 100/√3
Eksempel 6: Find værdien af tan θ hvis sin θ = 7/25 og sek θ = 25/24.
Løsning:
givet,
sin θ = 7/25
sek θ = 25/24
Vi ved det,
sek θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Vi har,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
Derfor, tan θ = 7/24
Eksempel 7: Find værdien af tan θ hvis cosec θ = 5/3, og θ er den første kvadrantvinkel.
Løsning:
Givet, cosec θ = 5/3
Fra de pythagoræiske identiteter har vi,
string.format javacosec2θ – barneseng2θ = 1
barneseng2θ = cosec2i – 1
barneseng θ = (5/3)2– 1 = (25/9) – 1 = 16/9
barneseng θ = ±√16/9 = ± 4/3
Da θ er den første kvadrantvinkel, er både cotangens- og tangentfunktioner positive.
barneseng θ = 4/3
Vi ved det,
barneseng θ = 1/tan θ
4/3 = 1/tanθ
tan θ = 3/4
Derfor, tan θ = 3/4
Eksempel 8: Find tan 3θ hvis sin θ = 3/7 og θ er den første kvadrantvinkel.
Løsning :
Givet, sin θ = 12/13
Fra de pythagoræiske identiteter, vi har,
uden2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Da θ er den første kvadrantvinkel, er cos θ positiv.
cos θ = 5/13
Vi ved det,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Derfor er tan θ = 12/5
Nu ved vi det,
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

