I den virkelige verden maskinelæring applikationer, er det almindeligt at have mange relevante funktioner, men kun en delmængde af dem kan observeres. Når man beskæftiger sig med variabler, der nogle gange er observerbare og nogle gange ikke, er det faktisk muligt at bruge de tilfælde, hvor denne variabel er synlig eller observeret, for at lære og lave forudsigelser for de tilfælde, hvor den ikke er observerbar. Denne tilgang omtales ofte som håndtering af manglende data. Ved at bruge de tilgængelige tilfælde, hvor variablen er observerbar, kan maskinlæringsalgoritmer lære mønstre og relationer fra de observerede data. Disse indlærte mønstre kan derefter bruges til at forudsige værdierne af variablen i tilfælde, hvor den mangler eller ikke kan observeres.

Forventningsmaksimeringsalgoritmen kan bruges til at håndtere situationer, hvor variabler er delvist observerbare. Når visse variabler er observerbare, kan vi bruge disse forekomster til at lære og estimere deres værdier. Derefter kan vi forudsige værdierne af disse variable i tilfælde, hvor det ikke er observerbart.

EM-algoritmen blev foreslået og navngivet i et banebrydende papir udgivet i 1977 af Arthur Dempster, Nan Laird og Donald Rubin. Deres arbejde formaliserede algoritmen og demonstrerede dens anvendelighed i statistisk modellering og estimering.

EM-algoritmen er anvendelig til latente variabler, som er variabler, der ikke er direkte observerbare, men som udledes af værdierne af andre observerede variabler. Ved at udnytte den kendte generelle form for sandsynlighedsfordelingen, der styrer disse latente variable, kan EM-algoritmen forudsige deres værdier.
EM-algoritmen fungerer som grundlaget for mange uovervågede klyngealgoritmer inden for maskinlæring. Det giver en ramme til at finde de lokale maksimale sandsynlighedsparametre for en statistisk model og udlede latente variabler i tilfælde, hvor data mangler eller er ufuldstændige.

Forventningsmaksimering (EM) Algoritme

Expectation-Maximization (EM) algoritmen er en iterativ optimeringsmetode, der kombinerer forskellige uovervågede maskinelæring algoritmer til at finde maksimal sandsynlighed eller maksimale posteriore estimater af parametre i statistiske modeller, der involverer uobserverede latente variabler. EM-algoritmen bruges almindeligvis til latente variable modeller og kan håndtere manglende data. Det består af et estimeringstrin (E-trin) og et maksimeringstrin (M-trin), der danner en iterativ proces for at forbedre modeltilpasningen.

• I E-trinnet beregner algoritmen de latente variable, dvs. forventningen til log-sandsynligheden ved hjælp af de aktuelle parameterestimater.
• I M-trinnet bestemmer algoritmen de parametre, der maksimerer den forventede log-sandsynlighed opnået i E-trinnet, og tilsvarende modelparametre opdateres baseret på de estimerede latente variable.

Forventningsmaksimering i EM-algoritme

Ved iterativt at gentage disse trin søger EM-algoritmen at maksimere sandsynligheden for de observerede data. Det bruges almindeligvis til uovervågede læringsopgaver, såsom clustering, hvor latente variabler udledes og har applikationer inden for forskellige områder, herunder maskinlæring, computersyn og naturlig sprogbehandling.

Nøgleord i forventningsmaksimeringsalgoritmen (EM).

Nogle af de mest almindeligt anvendte nøglebegreber i Expectation-Maximization (EM) Algorithm er som følger:

Latente variable: Latente variable er uobserverede variable i statistiske modeller, som kun kan udledes indirekte gennem deres virkninger på observerbare variable. De kan ikke måles direkte, men kan detekteres ved deres indvirkning på de observerbare variable. Sandsynlighed: Det er sandsynligheden for at observere de givne data givet modellens parametre. I EM-algoritmen er målet at finde de parametre, der maksimerer sandsynligheden. Log-Likelihood: Det er logaritmen af ​​sandsynlighedsfunktionen, som måler godheden af ​​tilpasning mellem de observerede data og modellen. EM-algoritmen søger at maksimere log-sandsynligheden. Maximum Likelihood Estimation (MLE): MLE er en metode til at estimere parametrene for en statistisk model ved at finde de parameterværdier, der maksimerer likelihood-funktionen, som måler, hvor godt modellen forklarer de observerede data. Posterior sandsynlighed: I sammenhæng med Bayesiansk inferens kan EM-algoritmen udvides til at estimere de maksimale a posteriori (MAP) estimater, hvor den posteriore sandsynlighed for parametrene beregnes baseret på den forudgående fordeling og sandsynlighedsfunktionen. Forventningstrin (E) : E-trinnet i EM-algoritmen beregner den forventede værdi eller posteriore sandsynlighed for de latente variable givet de observerede data og aktuelle parameterestimater. Det involverer at beregne sandsynligheden for hver latent variabel for hvert datapunkt. Maksimering (M) Trin: M-trinnet i EM-algoritmen opdaterer parameterestimaterne ved at maksimere den forventede log-sandsynlighed opnået fra E-trinnet. Det går ud på at finde de parameterværdier, der optimerer likelihood-funktionen, typisk gennem numeriske optimeringsmetoder. Konvergens: Konvergens refererer til tilstanden, når EM-algoritmen har nået en stabil løsning. Det bestemmes typisk ved at kontrollere, om ændringen i log-sandsynligheden eller parameterestimaterne falder under en foruddefineret tærskel.

Sådan fungerer forventningsmaksimeringsalgoritmen (EM):

Essensen af ​​Expectation-Maximization-algoritmen er at bruge de tilgængelige observerede data fra datasættet til at estimere de manglende data og derefter bruge disse data til at opdatere værdierne af parametrene. Lad os forstå EM-algoritmen i detaljer.

EM Algoritme Flowchart

Initialisering:
• Indledningsvis overvejes et sæt initialværdier for parametrene. Et sæt ufuldstændige observerede data gives til systemet med den antagelse, at de observerede data kommer fra en specifik model.
E-trin (forventningstrin): I dette trin bruger vi de observerede data til at estimere eller gætte værdierne af de manglende eller ufuldstændige data. Det bruges grundlæggende til at opdatere variablerne.
• Beregn den bageste sandsynlighed eller ansvar for hver latent variabel givet de observerede data og aktuelle parameterestimater.
• Estimer de manglende eller ufuldstændige dataværdier ved hjælp af de aktuelle parameterestimater.
• Beregn log-sandsynligheden for de observerede data baseret på de aktuelle parameterestimater og estimerede manglende data.
M-trin (maksimeringstrin): I dette trin bruger vi de komplette data, der er genereret i det foregående Forventningstrin, for at opdatere parametrenes værdier. Det bruges grundlæggende til at opdatere hypotesen.
• Opdater modellens parametre ved at maksimere den forventede fuldstændige datalogsandsynlighed opnået fra E-trinnet.
• Dette involverer typisk løsning af optimeringsproblemer for at finde de parameterværdier, der maksimerer log-sandsynligheden.
• Den specifikke optimeringsteknik, der anvendes, afhænger af problemets art og den anvendte model.
Konvergens: I dette trin kontrolleres det, om værdierne konvergerer eller ej, hvis ja, stop ellers gentag trin-2 og trin-3 dvs. Forventning – trin og Maksimering – trin indtil konvergensen indtræffer.
• Tjek for konvergens ved at sammenligne ændringen i log-sandsynlighed eller parameterværdierne mellem iterationer.
• Hvis ændringen er under en foruddefineret tærskel, skal du stoppe og betragte algoritmen som konvergeret.
• Ellers skal du gå tilbage til E-trinnet og gentage processen, indtil konvergens er opnået.

Forventnings-maksimeringsalgoritme Trin for trin implementering

Importer de nødvendige biblioteker

Python3

>

>

Generer et datasæt med to Gaussiske komponenter

Python3

>

>

Produktion :

Densitet Plot

Initialiser parametre

Python3

>

>

Udfør EM-algoritme

• Itererer for det angivne antal epoker (20 i dette tilfælde).
• I hver epoke beregner E-trinnet ansvar (gammaværdier) ved at evaluere de Gaussiske sandsynlighedstætheder for hver komponent og vægte dem med de tilsvarende proportioner.
• M-trinnet opdaterer parametrene ved at beregne det vægtede gennemsnit og standardafvigelsen for hver komponent

Python3

>

>

Produktion :

Epoke vs Log-sandsynlighed

Plot den endelige estimerede tæthed

Python3

>

tilfældig ikke i java

>

Produktion :

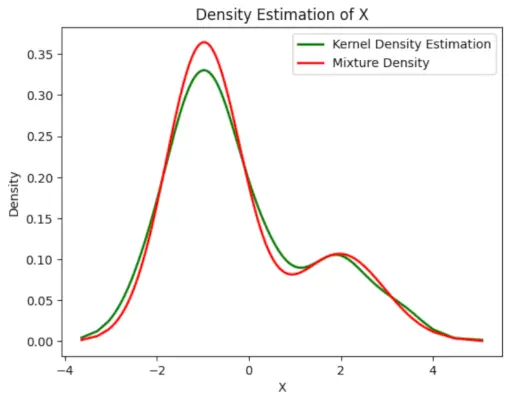
Estimeret tæthed

Ansøgninger af EM algoritme

• Det kan bruges til at udfylde de manglende data i en prøve.
• Det kan bruges som grundlag for uovervåget læring af klynger.
• Den kan bruges til at estimere parametrene for Hidden Markov Model (HMM).
• Det kan bruges til at opdage værdierne af latente variabler.

Fordele ved EM-algoritme

• Det er altid garanteret, at sandsynligheden vil stige med hver iteration.
• E-trinnet og M-trinnet er ofte ret nemt for mange problemer med hensyn til implementering.
• Løsninger på M-trinene findes ofte i den lukkede form.

Ulemper ved EM-algoritme

• Det har langsom konvergens.
• Det gør kun konvergens til det lokale optima.
• Det kræver både sandsynligheder fremad og bagud (numerisk optimering kræver kun fremadrettet sandsynlighed).