Er hvert rektangel en rombe? Rektangel er en todimensionel geometrisk figur afbildet af fire sider og fire hjørner. Et rektangel indeholder sider, således at længden af de modstående sider er lige store, og disse sider er parallelle med hinanden. Siderne deler et hjørne fra tilstødende sider med en vinkel på 90° mellem dem. Derfor er der fire rette vinkler i rektanglet.

Indholdsfortegnelse
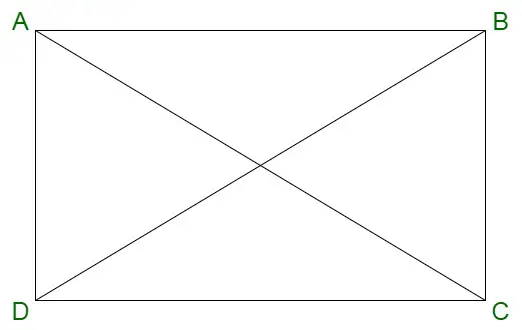
Rektangel
Egenskaberne for et rektangel er angivet nedenfor:
- Den har fire kanter og fire hjørner, kendt som hjørner.
- Diagonaler i et rektangel halverer hinanden.
- Arealet af et rektangel svarer til produktet af dets længde og bredde.
- Hvert toppunkt har en vinkel lig med 90O
- De modsatte sider af et rektangel er lige store og parallelle med hinanden.
- Omkreds svarer til det dobbelte af summen af dens længde og bredde.
- Summen af alle indvendige vinkler er lig med 360 grader
Omkredsen af et rektangel
Den totale forskydning dækket af at gå gennem rektanglets grænse kan betegnes som omkredsen. Da både længde og bredde er angivet med længdeenhed, måles omkredsen også i længdeenhed.
Omkreds kan betegnes med,
Omkreds, P = 2 (længde + bredde)
Areal af rektangel
Området dækket af en todimensionel geometrisk figur i et plan kaldes arealet af en figur. Således er arealet af et rektangel det område, der er inkluderet inden for dets grænser. Det måles i kvadratenheder. Arealet svarer til produktet af rektanglets længde og bredde.
Området kan betegnes med,
Areal, A = Længde × Bredde sq. enheder
Diagonal af en rektangelformel
Diagonaler af enhver geometrisk figur forbinder alternative hjørner. Længden af diagonaler af et rektangel kan beregnes ved hjælp af følgende formel, angivet med d,
d = sqrt{( l^2 + w^2)} hvor,
l = længden af rektanglet
w = rektanglets bredde
Læs i detaljer: Egenskaber for rektangel: Definition, formler, eksempler
Rhombus
En rhombus er også kendt som en firsidet firkant. Det anses for at være et særligt tilfælde af et parallelogram. En rombe indeholder parallelle modstående sider og lige store modsatte vinkler. En rhombus er også kendt under navnet diamant eller rhombus diamant. En rhombus indeholder alle siderne af en rhombus lige lange. Også diagonalerne på en rombe halverer hinanden i rette vinkler.
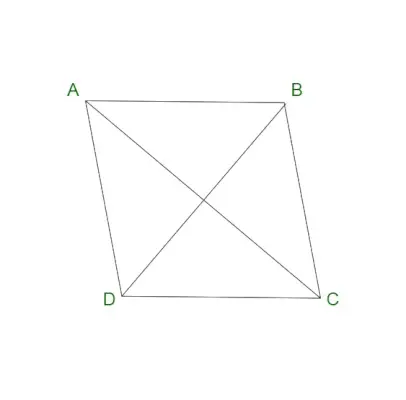
Egenskaber af en Rhombus
En rombe indeholder følgende egenskaber:
- En rombe indeholder alle lige sider.
- Diagonaler på en rombe halverer hinanden i rette vinkler.
- De modsatte sider af en rombe er parallelle i naturen.
- Summen af to tilstødende vinkler på en rombe er lig med 180O.
- Der er ingen indskrivende cirkel inden i en rombe.
- Der er ingen omskrivende cirkel omkring en rombe.
- Diagonalerne på en rombe fører til dannelsen af fire retvinklede trekanter.
- Disse trekanter er kongruente med hinanden.
- De modsatte vinkler på en rombe er lige store.
- Når du forbinder midtpunktet af siderne af en rombe, dannes et rektangel.
- Når midtpunkterne på halvdelen af diagonalen er forbundet, dannes en anden rombe.
Omkreds af Rhombus
Omkredsen af en rombe er defineret som den samlede længde af dens grænser, der danner figuren. Det kan også betegnes som den samlede summering af længden af fire sider af en rombe. Omkredsen af en rombe er defineret ved:
Omkreds, P = 4a enheder
hvor rhombus diagonaler er angivet med d1& d2og 'a' er siden.
Område af Rhombus
Arealet af romben er defineret som området indesluttet i et todimensionalt plan. Arealet af en rombe er ækvivalent med produktet af diagonaler på rombe divideret med 2. Arealet af romben kan defineres med følgende formel:
Areal, A =
frac{(d_1 imes d_2)}{2} kvm enhederhvor d1og d2er diagonalerne på en rombe.
Vi kan let bemærke, at hver rombe er et parallelogram, men det omvendte er ikke sandt. Et kvadrat kan betragtes som et specialtilfælde af en rombe, da det indeholder fire sider af lige længde. Et kvadrat har alle rette vinkler. Men alle vinklerne på en rombe er ikke nødvendigvis rette vinkler . Afslutningsvis kan en rombe indeholdende rette vinkler betragtes som en firkant. Derfor kan vi sige, at
- Alle romber er parallellogrammer.
- Alle parallelogrammer er ikke romber.
- Alle romber er ikke firkanter.
- Alle firkanter er romber.
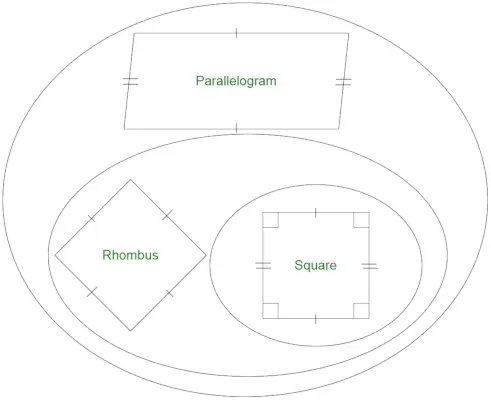
Er hvert rektangel en Rhombus?
Et rektangel er en geometrisk figur, der ikke indeholder alle lige sider. Et kvadrat er et specialtilfælde af rektangel med alle lige sider. Da vi ved, en rombe har alle lige sider. Sæt af rektangler og romber skærer kun hinanden i tilfælde af kvadrater. Derfor er rektanglet ikke en rombe.
vb og vb net

Hvorfor er en Rhombus et rektangel?
En rombe er et specialtilfælde af et rektangel. Da vi ved, at diagonalerne på en rombe skærer hinanden i lige store vinkler, mens diagonalerne i et rektangel er lige lange. Ved at forbinde midtpunkterne på siderne af en rombe dannes et rektangel.
Læs mere: Hvorfor er en rombe ikke en firkant?
Prøvespørgsmål – Er hvert rektangel en rombe
Spørgsmål 1. Beregn arealet af en rektangulær ramme, som har 6 tommer inde længde og er 3 tommer bred.
Løsning:
Da vi ved,
Arealet af et rektangel = (Længde × Bredde) kvadratenheder.
Ved at erstatte værdierne får vi,
arealet af rektangulær ramme = 6 × 3 = 18 kvadrattommer
Spørgsmål 2. Find længden af diagonalen af et rektangel, som har en længde på henholdsvis 12 cm og en bredde på 8 cm.
Løsning:
Vi ved,
Diagonal længde,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Spørgsmål 3. Find arealet af en rombe med de to diagonallængder d 1 og d 2 at være henholdsvis 6 cm og 12 cm.
Løsning:
Vi har,
Diagonal d1= 6 cm
Diagonal d2= 12 cm
Arealet af rhombus er givet ved,
A =
frac{(d_1 imes d_2)}{2} kvm enhederA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Derfor er arealet af rombe = 36 cm2.
Spørgsmål 4. Forskel mellem Rhombus og rektangel?
Løsning:
| Ejendom | Rhombus | Rektangel |
| Sider | Lige sider. | Modsatte sider er lige store. |
| Diagonaler | Diagonalerne halverer hinanden ved 90°. Diagonaler danner rette vinkler i midten. | Diagonalerne halverer hinanden i forskellige vinkler. Den ene vinkel er en stump vinkel, og den anden er en spids vinkel. Diagonaler danner forskellige vinkler i midten - en stump vinkel og en spids vinkel. |
| Vinkler | Modsatte vinkler er lige store. Tilstødende vinkler tilføjer op til 180°. | Modsatte og tilstødende vinkler er lige store. En vinkel dannet af de tilstødende sider af et rektangel er 90°. |
