Slet-funktionen bruges til at slette den angivne node fra et binært søgetræ. Vi skal dog slette en node fra et binært søgetræ på en sådan måde, at egenskaben for binært søgetræ ikke overtræder. Der er tre situationer med sletning af en node fra binært søgetræ.
Noden, der skal slettes, er en bladknude
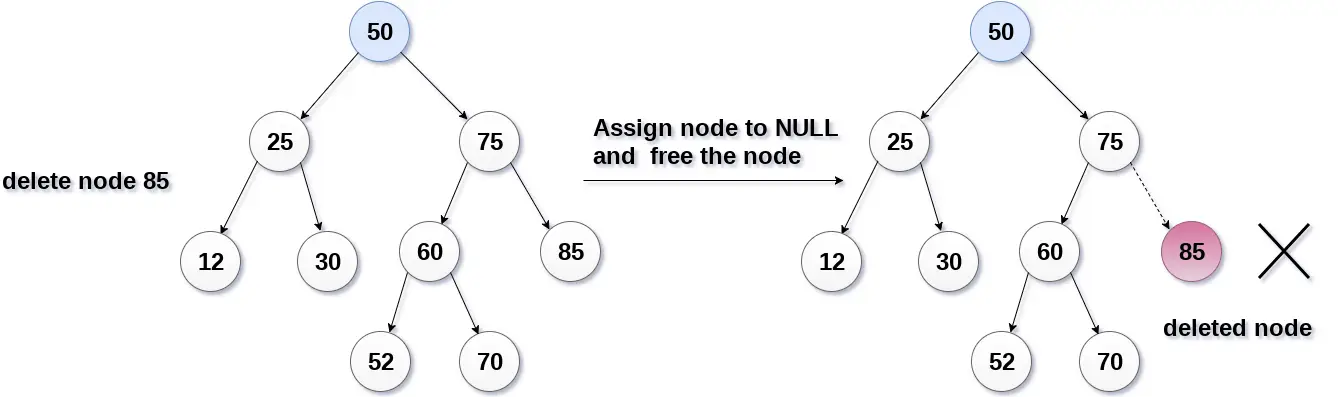
Det er det enkleste tilfælde, i dette tilfælde skal du udskifte bladknuden med NULL og ganske enkelt frigøre den tildelte plads.
I det følgende billede sletter vi noden 85, da noden er en bladknude, derfor vil noden blive erstattet med NULL og tildelt plads vil blive frigivet.
Noden, der skal slettes, har kun ét underordnet.
I dette tilfælde skal du erstatte noden med dens underordnede og slette den underordnede node, som nu indeholder den værdi, der skal slettes. Du skal blot udskifte den med NULL og frigøre den tildelte plads.
I det følgende billede skal knudepunktet 12 slettes. Den har kun ét barn. Noden vil blive erstattet med dens underordnede node, og den erstattede node 12 (som nu er bladnode) vil simpelthen blive slettet.

Noden, der skal slettes, har to børn.
Det er en lidt kompleks sag sammenlignet med to andre sager. Imidlertid erstattes knudepunktet, som skal slettes, med sin i rækkefølge efterfølger eller forgænger rekursivt, indtil nodeværdien (der skal slettes) er placeret på træets blad. Efter proceduren skal du erstatte noden med NULL og frigøre den tildelte plads.
I det følgende billede skal knudepunktet 50 slettes, som er træets rodknude. Træet i rækkefølge, vist nedenfor.
6, 25, 30, 50, 52, 60, 70, 75.
erstatte 50 med dens i rækkefølge efterfølger 52. Nu vil 50 blive flyttet til bladet af træet, som simpelthen vil blive slettet.

Algoritme
Slet (TRÆ, ITEM)
Skriv 'vare ikke fundet i træet' ANDERS HVIS VAREDATA
Slet(TRÆ->VENSTRE, ITEM)
ANDET HVIS VARE > TRÆ -> DATA
Slet(TRÆ -> HØJRE, VARE)
ANDET HVIS TRÆ -> VENSTRE OG TRÆ -> HØJRE
SET TEMP = findLargestNode(TRÆ -> VENSTRE)
INDSTIL TRÆ -> DATA = TEMP -> DATA
Slet(TRÆ -> VENSTRE, TEMP -> DATA)
ANDET
INDSTIL TEMP = TRÆ
HVIS TRÆ -> VENSTRE = NULL OG TRÆ -> HØJRE = NULL
SÆT TRÆ = NULL
ANDET HVIS TRÆ -> VENSTRE != NULL
SÆT TRÆ = TRÆ -> VENSTRE
ANDET
SÆT TRÆ = TRÆ -> HØJRE
[SLUT PÅ HVIS]
FRI TEMP
[SLUT PÅ HVIS]
Fungere:
void deletion(Node*& root, int item) { Node* parent = NULL; Node* cur = root; search(cur, item, parent); if (cur == NULL) return; if (cur->left == NULL && cur->right == NULL) { if (cur != root) { if (parent->left == cur) parent->left = NULL; else parent->right = NULL; } else root = NULL; free(cur); } else if (cur->left && cur->right) { Node* succ = findMinimum(cur- >right); int val = succ->data; deletion(root, succ->data); cur->data = val; } else { Node* child = (cur->left)? Cur- >left: cur->right; if (cur != root) { if (cur == parent->left) parent->left = child; else parent->right = child; } else root = child; free(cur); } } Node* findMinimum(Node* cur) { while(cur->left != NULL) { cur = cur->left; } return cur; } 