Vandrette linjer er defineret som linjer, der er parallelle med horisonten eller jorden, deraf navnet vandret linje . Vandret linje har nul hældning, dvs. hældningsvinklen for disse linjer er nul grader. Hvis de vandrette linjer er tegnet på de kartesiske planer, skærer de kun langs y-aksen, da de altid er parallelle med x-aksen og aldrig skærer den.
I denne artikel vil vi lære om den vandrette linje, dens egenskaber, hældningen af den vandrette linje, ligningen for den vandrette linje, eksempler og ofte stillede spørgsmål relateret til de vandrette linjer og andre i detaljer.
Indholdsfortegnelse
- Horisontal linje definition
- Hældning af vandret linje
- Tegning af en vandret linje
- Horisontal linjeligning
- Horisontal linjetest
- Vandrette og lodrette linjer
- Forskelle mellem lodrette linjer og vandrette linjer
- Kort note om vandret linje
- Eksempler på vandret linje
Horisontal linjedefinition
Vi ved, at en linje er en lige vej, der forbinder to eller flere to punkter og løber op til det uendelige. Således definerer vi vandrette linjer som linjer, der er parallelle med jorden eller horisonten og er i konstant højde fra jorden.
Hvis vi plotter disse linjer på det kartesiske system, er disse linjer de linjer, der ikke har nogen skæring på x-aksen, men som har en skæring på y-aksen. Vandrette linjer har nul hældning, dvs. de har nul vinkel med x-aksen eller jorden.
Vandrette linjer danner bunden af de forskellige objekter, former og figurer, som vi studerer i geometri. Antag at vi skal tegne et rektangel, kvadrat, trekant, trapez , osv., så er bunden af disse figurer for det meste vandrette linjer. Vi observerer også vandrette løgne i det virkelige liv, da linjerne på gulvet og taget af rummene, bunden af trappen osv. også er lavet af de vandrette linjer.
Disse linjer er også kendt som soveliner, da de ikke har nogen lodret bevægelse og altid forbliver i en konstant højde fra jorden. Billedet tilføjet nedenfor viser den vandrette linje.
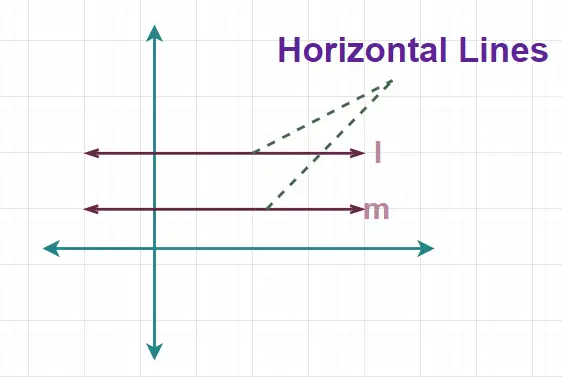
Her, i figuren tilføjet ovenfor, er linjer l og m vandrette linjer.
Hældning af vandret linje
Vi har allerede nævnt, at hældningen af den vandrette linje er nul . Lad os nu lære, hvordan hældningen af den vandrette linje er nul. Vi beregner hældningen af en vandret linje ved at bruge formlen,
Hældning = Stig/løb
ELLER
Linjehældning = Ændring i y-koordinat/Ændring i x-koordinat
Hvor stigning er højden opnået af linjen, mens den løber fra venstre mod højre, da vi allerede ved, at den vandrette linje er parallel med x-aksen og altid er i konstant højde, så siger vi, at disse linjer har nul stigning, så hældningen af disse linjer er,
Hældning = 0/Kørsel = 0
Således konkluderes det, at hældningen af den vandrette linje er nul.
Tegning af en vandret linje
Vandrette linjer tegnes nemt ved at bruge de trin, der er beskrevet nedenfor,
Trin 1: Tag et punkt på det kartesiske plan, som vi skal finde den vandrette linje for. Antag, at punktet er (1, 2)
Trin 2: Markerer punktets y-koordinat. I dette tilfælde er y-koordinaten 2.
Trin 3: Marker andre punkter, hvor y-koordinaten er den samme som punktet i trin 1. Lad de andre punkter være (-2, 2), (0, 2) og (7, 2)
Trin 4: Forbind alle punkterne for at få et linjestykke, og stræk dem ud på begge sider for at få en vandret linje.
Dette er den nødvendige vandrette linje, der går gennem punktet (1, 2) og har en hældning på nul.

Horisontal linjeligning
Vi ved, at linjens ligning i 2-D koordinatsystemet er,
y = mx + c
Hvor,
- m er linjens hældning
- c er skæringspunktet på y-aksen
Vi ved, at for den vandrette linje er hældningen nul. Ved at erstatte denne værdi i ovenstående ligning får vi ligningen for den vandrette linje til at være,
y = 0x + c
y = c
Hvor c er en konstant.
Således er ovenstående ligning y = c ligningen for den vandrette linje.
Denne ligning betyder, at den vandrette linje er en linje, der går gennem alle punkter i den kartesiske, hvor y-koordinaten er lig med 'c'. Dette linjesnit har ingen x-koordinat, og derfor skærer denne linje aldrig x-aksen, og den skærer y-aksen ved punktet (0, c).
Således kan vi sige, at ligningen for den vandrette linje er, y = c(konstant), og den går gennem punktet (a, c), hvor a kan tage en hvilken som helst værdi og c altid er konstant.
Horisontal linjetest
En test, der bruges til at definere, om en funktion er en en-til-en-funktion eller ej, er den vandrette linjetest. I den vandrette linjetest tegner vi en vandret linje, der går gennem et hvilket som helst punkt på funktionen, og hvis linjerne skærer funktionen på et hvilket som helst andet punkt, så er funktionen IKKE en en-til-en funktion. For at en funktion skal være en-til-en, skal den bestå den vandrette linjetest, dvs. at enhver vandret linje kun skal skære funktionen én gang.
Vi ved, at en-til-en-funktioner er de funktioner, hvor vi for hver værdi af x kun har én værdi af y. Så hvis den vandrette linje passerer gennem funktionen og kun skærer den én gang, kan vi sige, at for den unikke værdi af y, har vi en unik værdi af x. Men hvis den vandrette linje skærer funktionen mere end én gang, får vi to værdier for den unikke værdi af y, hvilket ikke er tilfældet for en-til-en-funktionen.
Horisontal linjetest hjælper os med at afgøre, om en funktion er en en-en-funktion. Dette kan forstås ved hjælp af billedet tilføjet nedenfor.

På det første billede er funktionen en-til-en, fordi den vandrette linje kun passerer gennem ét punkt i funktionen.
På det andet billede er funktionen IKKE en-til-en, da den vandrette linje går gennem mere end et punkt i funktionen.
Vandrette og lodrette linjer
Vandrette linjer er linjer, der er parallelle med jorden eller horisonten. Disse linjer kaldes også for sovelinjer. I det kartesiske system er disse linjer parallelle med x-aksen, mens det for de lodrette linjer er de linjer, der er vinkelrette på de vandrette linjer, de kaldes de stående linjer. og er parallelle med y-aksen i det kartesiske system.
Vandrette linjer er de linjer, der løber fra venstre mod højre i det kartesiske system, mens lodrette linjer er de linjer, der løber op og ned i det kartesiske system.
Lodrette og vandrette linjer er vinkelrette på hinanden. Billedet tilføjet nedenfor viser en lodret og vandret linje.

Forskelle mellem lodrette linjer og vandrette linjer
Forskellene mellem lodrette linjer og vandrette linjer kan let forstås ved at studere tabellen tilføjet nedenfor.
| Vandret linje | Lodret linje |
|---|---|
| Disse linjer er parallelle med jorden eller horisonten. | Disse linjer er vinkelret til jorden eller horisonten. |
| Hældningen af den vandrette linje er nul. | Hældningen af den lodrette linje er udefineret. |
| Vandret linje lavede en vinkel på nul grader med horisonten. | Lodret linje lavede en vinkel på 90 grader med horisonten. |
| Ligningen for den vandrette linje, der går gennem punktet (h, k), er, y = k | Ligningen for den lodrette linje, der går gennem punktet (h, k), er, x = h |
| Vandrette linjer er parallelle med x-aksen i det kartesiske system. | Lodrette linjer er parallelle med y-aksen i det kartesiske system. |
| Eksempler der repræsenterer de vandrette linjer er,
| Eksempler der repræsenterer de lodrette linjer er,
|
Kort note om vandret linje
En vandret linje i matematik er perfekt plan, parallel med horisonten. Den løber fra venstre mod højre og har en hældning på 0. I geometri er den repræsenteret som en lige linje, der forbinder to punkter i samme højde på et plan. Ligningen for en vandret linje er af formen (y = k), hvor (k) er en konstant værdi, der repræsenterer højden af linjen på y-aksen.
Læs mere:
- Typer af linjer
- Parallelle linier
- Hvordan tilføjer man vandret linje i HTML?
- Hvordan bruger man komplet vandret linjerum i HTML?
- Sådan tegner du vandrette og lodrette linjer i en Android-app ved hjælp af XML
Eksempler på vandret linje
Eksempel 1: Find ligningen for den vandrette linje, der går gennem punktet (1, -1).
Løsning:
Vi ved, at hældningen af den vandrette linje er m = 0.
Givet punkt (1, -1)
Ligning for linjen, der går gennem et punkt (x1, og1) og har en hældning (m) er,
og – og1= m(x – x1)
Ved at erstatte værdierne i ovenstående ligning får vi,
y – (-1) = 0(x – 1)
og + 1 = 0
y = -1
Således er ligningen for den vandrette linje, der går gennem punktet (1, -1), y = -1
Eksempel 2: Find ligningen for den vandrette linje, der går gennem punktet (5, 9).
Løsning:
Vi ved, at hældningen af den vandrette linje er m = 0.
Givet punkt (5, 9)
Ligning for linjen, der går gennem et punkt (x1, og1) og har en hældning (m) er,
og – og1= m(x – x1)
Ved at erstatte værdierne i ovenstående ligning får vi,
y – (9) = 0(x – 5)
java læs fil linje for linjeog – 9 = 0
y = 9
Således er ligningen for den vandrette linje, der går gennem punktet (5, 9), y = 9
Eksempel 3: Find ligningen for den vandrette linje, når y-skæringspunktet for linjen er 5.
Løsning:
Ligningen for den vandrette linje er,
y = k
hvor k er y-afskæring
Givet
- k = 5
Ligning for den vandrette linje,
y = 5
Således er ligningens vandrette linje med y-skæringspunktet som 5, y = 5
Eksempel 4: Find ligningen for den vandrette linje, når y-skæringspunktet for linjen er -11/3.
Løsning:
Ligningen for den vandrette linje er,
y = k
hvor k er y-afskæring
Givet
- k = -11/3
Ligning for den vandrette linje,
y = -11/3
3y = -11
3y + 11 = 0
Således er ligningens vandrette linje med y-skæringspunktet som -11/3, 3y + 11 = 0
Vandrette linjer – ofte stillede spørgsmål
Hvad er vandrette linjer?
Vandrette linjer er linjer, der er parallelle med horisonten eller jorden. I det kartesiske system er vandrette linjer parallelle med x-aksen.
Hvad er ligningen for den vandrette linje?
Ligningen for den vandrette linje er,
y = k
hvor k er skæringspunktet på y-aksen.
Hvad er hældningen af en vandret linje?
Hældningen af den vandrette linje er altid lig nul, da de danner nul graders vinkel med x-aksen.
Hvad er eksempler på vandrette linjer?
Eksempler der repræsenterer de vandrette linjer er,
- Lige vej
- Bunden af trappen
- Base af enhver figur osv.
Hvad hedder de vandrette linjer på kloden?
Vandrette linjer, der løber på kloden, kaldes breddegrader, og de løber parallelt med ækvator.
Hvad er egenskaberne ved vandrette linjer?
Forskellige egenskaber ved de vandrette linjer er,
- De er parallelle med jorden, horisonten og x-aksen.
- De er vinkelrette på y-aksen.
- Hældningen af den vandrette linje er nul osv.
Hvilken linje er lodret og vandret?
En lodret linje er parallel med y-aksen og løber lige op og ned i et koordinatplan, mens en vandret linje er parallel med x-aksen og løber lige til venstre og højre.
Hvad er hældningen af en vandret og lodret linje?
Hældningen af en linje angiver dens stejlhed og retning. Det beregnes som forholdet mellem den lodrette ændring og den vandrette ændring mellem to punkter på linjen.
Hvad er de vandrette og lodrette punktlinjer?
Vandrette linjer strækker sig fra venstre mod højre eller højre mod venstre og løber parallelt med x-aksen, mens lodrette linjer strækker sig op og ned og løber parallelt med y-aksen. Disse to typer linjer er vinkelrette på hinanden.
