EN Binær bunke er en komplet binært træ som bruges til at gemme data effektivt for at få max- eller min-elementet baseret på dets struktur.
En binær bunke er enten Min Heap eller Max Heap. I en Min Binary Heap skal nøglen ved roden være minimum blandt alle nøgler, der findes i Binary Heap. Den samme egenskab skal være rekursivt sand for alle noder i binært træ. Max Binary Heap ligner MinHeap.
Eksempler på Min Heap:
10 10
//
20 100 15 30
/ / /
30 40 50 100 40
Hvordan er Binary Heap repræsenteret?
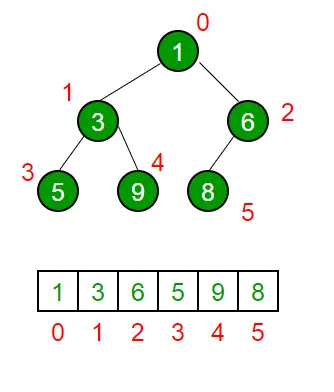
En binær bunke er en Komplet binært træ . En binær heap er typisk repræsenteret som en matrix.
- Rodelementet vil være ved Arr[0].
- Nedenstående tabel viser indekser for andre noder for ithnode, dvs. Arr[i]:
| Arr[(i-1)/2] | Returnerer den overordnede node |
| Arr[(2*i)+1] | Returnerer den venstre underordnede node |
| Arr[(2*i)+2] | Returnerer den rigtige underordnede node |
Traversalmetoden, der bruges til at opnå Array-repræsentation, er Level Order Traversal . Vær sød at henvise til Array-repræsentation af binær bunke for detaljer.
Operationer på Heap:
Nedenfor er nogle standardoperationer på min heap:
- getMin(): Det returnerer rodelementet i Min Heap. Tidskompleksiteten af denne operation er O(1) . I tilfælde af en maxheap ville det være getMax() .
- extractMin() : Fjerner minimumselementet fra MinHeap. Tidskompleksiteten af denne operation er O(log N) da denne operation skal vedligeholde heap-egenskaben (ved at kalde heapify() ) efter at have fjernet roden.
- formindsk nøgle() : Formindsker nøglens værdi. Tidskompleksiteten af denne operation er O(log N) . Hvis den reducerede nøgleværdi for en node er større end nodens forælder, behøver vi ikke at gøre noget. Ellers er vi nødt til at krydse op for at reparere den krænkede bunkeejendom.
- indsæt() : Indsættelse af en ny nøgle tager O(log N) tid. Vi tilføjer en ny nøgle for enden af træet. Hvis den nye nøgle er større end dens forælder, behøver vi ikke at gøre noget. Ellers er vi nødt til at krydse op for at reparere den krænkede bunkeejendom.
- slet() : Det tager også at slette en nøgle O(log N) tid. Vi erstatter nøglen, der skal slettes med minimum uendelig ved at ringe formindsk nøgle() . Efter reductionKey() skal minus uendelige værdi nå root, så vi kalder extractMin() for at fjerne nøglen.
Nedenfor er implementeringen af grundlæggende heap-operationer.
C++
// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>'
Overflow: Could not insertKey
'>;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest != i) { swap(&harr[i], &harr[smallest]); MinHeapify(smallest); } } // A utility function to swap two elements void swap(int *x, int *y) { int temp = *x; *x = *y; *y = temp; } // Driver program to test above functions int main() { MinHeap h(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); cout << h.extractMin() << ' '; cout << h.getMin() << ' '; h.decreaseKey(2, 1); cout << h.getMin(); return 0; }> |
>
>
kat timpf højde
Java
// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0> && heapArray[i] swap(heapArray, i, parent(i)); i = parent(i); } return true; } // Decreases value of given key to new_val. // It is assumed that new_val is smaller // than heapArray[key]. public void decreaseKey(int key, int new_val) { heapArray[key] = new_val; while (key != 0 && heapArray[key] swap(heapArray, key, parent(key)); key = parent(key); } } // Returns the minimum key (key at // root) from min heap public int getMin() { return heapArray[0]; } // Method to remove minimum element // (or root) from min heap public int extractMin() { if (current_heap_size <= 0) { return Integer.MAX_VALUE; } if (current_heap_size == 1) { current_heap_size--; return heapArray[0]; } // Store the minimum value, // and remove it from heap int root = heapArray[0]; heapArray[0] = heapArray[current_heap_size - 1]; current_heap_size--; MinHeapify(0); return root; } // This function deletes key at the // given index. It first reduced value // to minus infinite, then calls extractMin() public void deleteKey(int key) { decreaseKey(key, Integer.MIN_VALUE); extractMin(); } // A recursive method to heapify a subtree // with the root at given index // This method assumes that the subtrees // are already heapified private void MinHeapify(int key) { int l = left(key); int r = right(key); int smallest = key; if (l smallest = l; } if (r smallest = r; } if (smallest != key) { swap(heapArray, key, smallest); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } // Driver Code class MinHeapTest { public static void main(String[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); System.out.print(h.extractMin() + ' '); System.out.print(h.getMin() + ' '); h.decreaseKey(2, 1); System.out.print(h.getMin()); } } // This code is contributed by rishabmalhdijo> |
>
>
Python
streng array c
# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>self>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if> (l heapArray[l] { smallest = l; } if (r heapArray[r] { smallest = r; } if (smallest != key) { Swap(ref heapArray[key], ref heapArray[smallest]); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] { increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } static class MinHeapTest{ // Driver code public static void Main(string[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); Console.Write(h.extractMin() + ' '); Console.Write(h.getMin() + ' '); h.decreaseKey(2, 1); Console.Write(h.getMin()); } } // This code is contributed by // Dinesh Clinton Albert(dineshclinton)> |
>
række af strenge i c
>
Javascript
// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]] this.MinHeapify(smallest); } } } let h = new MinHeap(); h.insert(3); h.insert(2); h.deleteKey(1); h.insert(15); h.insert(5); h.insert(4); h.insert(45); console.log(h.extractMin() + ' '); console.log(h.getMin() + ' '); h.decreaseKey(2, 1); console.log(h.extractMin());> |
>
>Produktion
2 4 1>
Anvendelser af Heaps:
- Dynge sortering : Heap Sort bruger Binary Heap til at sortere et array i O(nLogn) tid.
- Prioritetskø: Prioritetskøer kan implementeres effektivt ved hjælp af Binary Heap, fordi den understøtter insert(), delete() og extractmax(), reductionKey() operationer i O(log N) tid. Binomial Heap og Fibonacci Heap er variationer af Binary Heap. Disse variationer udfører forening også effektivt.
- Graph Algorithms: Prioritetskøerne bruges især i Graph Algorithms som Dijkstras korteste vej og Prim's Minimum Spanning Tree .
- Mange problemer kan løses effektivt ved hjælp af Heaps. Se f.eks. følgende. en) K'th største element i et array . b) Sorter en næsten sorteret matrix/ c) Flet K sorterede arrays .
Relaterede links:
- Kodningspraksis på Heap
- Alle artikler om Heap
- PriorityQueue: Binær heap-implementering i Java-bibliotek
