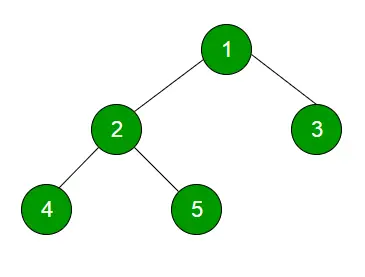
Level Order Traversal teknik er defineret som en metode til at krydse et træ, således at alle noder, der er til stede i samme niveau, gennemløbes fuldstændigt, før de krydser det næste niveau.

Eksempel:
Anbefalet praksis Gennemgang af ordrer på niveau Prøv det!Input:
Produktion:
1
23
Fire. Fem
Hvordan fungerer Level Order Traversal?
Hovedideen med niveaurækkefølgegennemgang er at krydse alle knuderne på et lavere niveau, før du flytter til nogen af knudepunkterne på et højere niveau. Dette kan gøres på en af følgende måder:
- den naive (finder højden af træet og krydser hvert niveau og udskriver noderne på det niveau)
- effektivt at bruge en kø.
Level Order Traversal (naiv tilgang):
Find højde af træ. Kør derefter en rekursiv funktion for hvert niveau ved at opretholde den aktuelle højde. Når niveauet for en node matcher, skal du udskrive den node.
Nedenfor er implementeringen af ovenstående tilgang:
C++ // Recursive CPP program for level // order traversal of Binary Tree #include using namespace std; // A binary tree node has data, // pointer to left child // and a pointer to right child class node { public: int data; node *left, *right; }; // Function prototypes void printCurrentLevel(node* root, int level); int height(node* node); node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(node* root, int level) { if (root == NULL) return; if (level == 1) cout << root->data<< ' '; else if (level>1) { printCurrentLevel(rod->venstre, niveau - 1); printCurrentLevel(root->right, level - 1); } } // Beregn 'højden' af et træ -- antallet af // noder langs den længste vej fra rodknuden // ned til den fjerneste bladknude. int height(node* node) { if (node == NULL) return 0; else { // Beregn højden af hvert undertræ int lheight = height(node->venstre); int højre = højde(node->højre); // Brug den større hvis (lheight> rheight) { return (lheight + 1); } andet { return (højre + 1); } } } // Hjælpefunktion, der tildeler // en ny node med de givne data og // NULL venstre og højre pointere. node* newNode(int data) { node* Node = new node(); Node->data = data; Node->venstre = NULL; Node->right = NULL; returnere (Node); } // Driverkode int main() { node* root = newNode(1); root->venstre = nyNode(2); root->right = newNode(3); root->venstre->venstre = nyNode(4); root->venstre->højre = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; } // This code is contributed by rathbhupendra> C // Recursive C program for level // order traversal of Binary Tree #include #include // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node *left, *right; }; // Function prototypes void printCurrentLevel(struct node* root, int level); int height(struct node* node); struct node* newNode(int data); // Function to print level order traversal a tree void printLevelOrder(struct node* root) { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Print nodes at a current level void printCurrentLevel(struct node* root, int level) { if (root == NULL) return; if (level == 1) printf('%d ', root->data); else if (niveau> 1) { printCurrentLevel(rod->venstre, niveau - 1); printCurrentLevel(root->right, level - 1); } } // Beregn 'højden' af et træ -- antallet af // noder langs den længste sti fra rodknuden // ned til den fjerneste bladknude int height(struct node* node) { if (node) == NULL) returner 0; else { // Beregn højden af hvert undertræ int lheight = height(node->venstre); int højre = højde(node->højre); // Brug den større hvis (lheight> rheight) return (lheight + 1); ellers retur (højre + 1); } } // Hjælpefunktion, der allokerer en ny node med de // givne data og NULL venstre og højre pointere. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); node->data = data; node->venstre = NULL; node->right = NULL; returnere (knudepunkt); } // Driverprogram til at teste ovenstående funktioner int main() { struct node* root = newNode(1); root->venstre = nyNode(2); root->right = newNode(3); root->venstre->venstre = nyNode(4); root->venstre->højre = newNode(5); printf('Niveauordensgennemgang af binært træ er
'); printLevelOrder(rod); retur 0; }> Java // Recursive Java program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { int data; Node left, right; public Node(int item) { data = item; left = right = null; } } class BinaryTree { // Root of the Binary Tree Node root; public BinaryTree() { root = null; } // Function to print level order traversal of tree void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number of // nodes along the longest path from the root node // down to the farthest leaf node. int height(Node root) { if (root == null) return 0; else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rheight) return (lheight + 1); ellers retur (højre + 1); } } // Udskriv noder på det aktuelle niveau void printCurrentLevel(Node rod, int niveau) { if (root == null) return; if (niveau == 1) System.out.print(root.data + ' '); else if (niveau> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, niveau - 1); } } // Driverprogram til at teste ovenstående funktioner public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = ny Node(1); tree.root.left = ny node(2); tree.root.right = ny node(3); tree.root.left.left = ny Node(4); tree.root.left.right = ny node(5); System.out.println('Niveaurækkefølgegennemgang af' + 'binært træ er '); træ.printLevelOrder(); } }> Python # Recursive Python program for level # order traversal of Binary Tree # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Function to print level order traversal of tree def printLevelOrder(root): h = height(root) for i in range(1, h+1): printCurrentLevel(root, i) # Print nodes at a current level def printCurrentLevel(root, level): if root is None: return if level == 1: print(root.data, end=' ') elif level>1: printCurrentLevel(root.left, level-1) printCurrentLevel(root.right, level-1) # Beregn højden af et træ - antallet af noder # langs den længste vej fra rodknuden ned til # det fjerneste blad node def height(node): hvis node er Ingen: returner 0 andet: # Beregn højden af hvert undertræ lheight = height(node.left) rheight = height(node.right) # Brug den større hvis lheight> rheight: returner lheight+1 else: return rheight+1 # Driverprogram til at teste ovenstående funktion hvis __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) rod. left.left = Node(4) root.left.right = Node(5) print('Niveaurækkefølgegennemgang af binært træ er -') printLevelOrder(rod) # Denne kode er bidraget af Nikhil Kumar Singh(nickzuck_007)> C# // Recursive c# program for level // order traversal of Binary Tree using System; // Class containing left and right // child of current node and key value public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = right = null; } } class GFG { // Root of the Binary Tree public Node root; public void BinaryTree() { root = null; } // Function to print level order // traversal of tree public virtual void printLevelOrder() { int h = height(root); int i; for (i = 1; i <= h; i++) { printCurrentLevel(root, i); } } // Compute the 'height' of a tree -- // the number of nodes along the longest // path from the root node down to the // farthest leaf node. public virtual int height(Node root) { if (root == null) { return 0; } else { // Compute height of each subtree int lheight = height(root.left); int rheight = height(root.right); // use the larger one if (lheight>rheight) { return (lheight + 1); } andet { return (højre + 1); } } } // Udskriv noder på det nuværende niveau public virtual void printCurrentLevel(Node rod, int niveau) { if (root == null) { return; } if (niveau == 1) { Console.Write(root.data + ' '); } else if (niveau> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, niveau - 1); } } // Driver Code public static void Main(string[] args) { GFG tree = new GFG(); tree.root = ny Node(1); tree.root.left = ny node(2); tree.root.right = ny node(3); tree.root.left.left = ny Node(4); tree.root.left.right = ny node(5); Console.WriteLine('Niveaurækkefølgegennemgang ' + 'af binært træ er '); træ.printLevelOrder(); } } // Denne kode er bidraget af Shrikant13> Javascript // Recursive javascript program for level // order traversal of Binary Tree // Class containing left and right child of current // node and key value class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Root of the Binary Tree var root= null; // Function to print level order traversal of tree function printLevelOrder() { var h = height(root); var i; for (i = 1; i <= h; i++) printCurrentLevel(root, i); } // Compute the 'height' of a tree -- the number // of nodes along the longest path // from the root node down to the farthest leaf node. function height(root) { if (root == null) return 0; else { // Compute height of each subtree var lheight = height(root.left); var rheight = height(root.right); // Use the larger one if (lheight>rheight) return (lheight + 1); ellers retur (højre + 1); } } // Udskriv noder på det aktuelle niveau funktion printCurrentLevel(root , level) { if (root == null) return; if (niveau == 1) console.log(root.data + ' '); else if (niveau> 1) { printCurrentLevel(root.left, level - 1); printCurrentLevel(root.right, niveau - 1); } } // Driverprogram til at teste ovenstående funktioner root = new Node(1); root.left = ny Node(2); root.right = ny Node(3); root.left.left = ny node(4); root.left.right = ny node(5); console.log('Niveaurækkefølgegennemgang af binært træ er '); printLevelOrder(); // Denne kode er bidraget af umadevi9616> Produktion
Level Order traversal of binary tree is 1 2 3 4 5>
Tidskompleksitet: O(N), hvor N er antallet af noder i det skæve træ.
Hjælpeplads: O(1) Hvis rekursionsstakken betragtes, er pladsen O(N).
algoritme for bfs
Level Order Traversal vha Kø
Vi er nødt til at besøge noderne på et lavere niveau før en hvilken som helst node på et højere niveau, denne idé er ret lig den i en kø. Skub noderne på et lavere niveau i køen. Når en node er besøgt, skal du åbne den node fra køen og skubbe barnet til den node i køen.
Dette sikrer, at noden på et lavere niveau besøges før enhver node på et højere niveau.
Nedenfor er implementeringen af ovenstående tilgang:
C++ // C++ program to print level order traversal #include using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // Iterative method to find height of Binary Tree void printLevelOrder(Node* root) { // Base Case if (root == NULL) return; // Create an empty queue for level order traversal queueq; // Sæt Root i kø og initialiser højden q.push(root); while (q.empty() == false) { // Udskriv forsiden af køen og fjern den fra køen Node* node = q.front(); cout<< node->data<< ' '; q.pop(); // Enqueue left child if (node->venstre != NULL) q.push(node->venstre); // Enqueue right child if (node->right != NULL) q.push(node->right); } } // Hjælpefunktion til at oprette en ny trænode Node* newNode(int data) { Node* temp = new Node; temp->data = data; temp->venstre = temp->højre = NULL; retur temp; } // Driverprogram til at teste ovenstående funktioner int main() { // Lad os oprette binært træ vist i ovenstående diagram Node* root = newNode(1); root->venstre = nyNode(2); root->right = newNode(3); root->venstre->venstre = nyNode(4); root->venstre->højre = newNode(5); cout<< 'Level Order traversal of binary tree is
'; printLevelOrder(root); return 0; }> C // Iterative Queue based C program // to do level order traversal // of Binary Tree #include #include #define MAX_Q_SIZE 500 // A binary tree node has data, // pointer to left child // and a pointer to right child struct node { int data; struct node* left; struct node* right; }; // Function prototypes struct node** createQueue(int*, int*); void enQueue(struct node**, int*, struct node*); struct node* deQueue(struct node**, int*); // Given a binary tree, print its nodes in level order // using array for implementing queue void printLevelOrder(struct node* root) { int rear, front; struct node** queue = createQueue(&front, &rear); struct node* temp_node = root; while (temp_node) { printf('%d ', temp_node->data); // Enqueue left child if (temp_node->left) enQueue(queue, &rear, temp_node->venstre); // Enqueue right child if (temp_node->right) enQueue(queue, &rear, temp_node->right); // Dequeue node og gør den temp_node temp_node = deQueue(queue, &front); } } // Hjælpefunktioner struct node** createQueue(int* front, int* rear) { struct node** queue = (struct node**)malloc( sizeof(struct node*) * MAX_Q_SIZE); *front = *bagside = 0; returkø; } void enQueue(struct node** queue, int* rear, struct node* new_node) { queue[*rear] = new_node; (*bag)++; } struct node* deQueue(struct node** kø, int* front) { (*front)++; returkø[*front - 1]; } // Hjælpefunktion, der tildeler en ny node med de // givne data og NULL venstre og højre pointere. struct node* newNode(int data) { struct node* node = (struct node*)malloc(sizeof(struct node)); node->data = data; node->venstre = NULL; node->right = NULL; returnere (knudepunkt); } // Driverprogram til at teste ovenstående funktioner int main() { struct node* root = newNode(1); root->venstre = nyNode(2); root->right = newNode(3); root->venstre->venstre = nyNode(4); root->venstre->højre = newNode(5); printf('Niveauordensgennemgang af binært træ er
'); printLevelOrder(rod); retur 0; }> Java // Iterative Queue based Java program // to do level order traversal // of Binary Tree import java.util.LinkedList; import java.util.Queue; // Class to represent Tree node class Node { int data; Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order // using array for implementing queue void printLevelOrder() { Queuekø = ny LinkedList(); queue.add(rod); mens (!queue.isEmpty()) { // poll() fjerner det nuværende hoved. Node tempNode = queue.poll(); System.out.print(tempNode.data + ' '); // Enqueue left child if (tempNode.left != null) { queue.add(tempNode.left); } // Enqueue right child if (tempNode.right != null) { queue.add(tempNode.right); } } } public static void main(String args[]) { // Oprettelse af et binært træ og indtastning af // noderne BinaryTree tree_level = new BinaryTree(); tree_level.root = ny node(1); tree_level.root.left = ny node(2); tree_level.root.right = ny node(3); tree_level.root.left.left = ny node(4); tree_level.root.left.right = ny node(5); System.out.println('Niveaurækkefølgegennemgang af binært træ er - '); tree_level.printLevelOrder(); } }> Python # Python program to print level # order traversal using Queue # A node structure class Node: # A utility function to create a new node def __init__(self, key): self.data = key self.left = None self.right = None # Iterative Method to print the # height of a binary tree def printLevelOrder(root): # Base Case if root is None: return # Create an empty queue # for level order traversal queue = [] # Enqueue Root and initialize height queue.append(root) while(len(queue)>0): # Udskriv forrest i køen og # fjern det fra køen print(queue[0].data, end=' ') node = queue.pop(0) # Sæt venstre underordnet i kø, hvis node.left ikke er Ingen: queue.append(node.left) # Sæt højre underord i kø, hvis node.right ikke er Ingen: queue.append(node.right) # Driver Program til at teste ovenstående funktion hvis __navn__ == '__main__': root = Node(1) ) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.left.right = Node(5) print('Niveaurækkefølgegennemgang af binært træ er - ') printLevelOrder(root) # Denne kode er bidraget af Nikhil Kumar Singh(nickzuck_007)> C# // Iterative Queue based C# program // to do level order traversal // of Binary Tree using System; using System.Collections.Generic; // Class to represent Tree node public class Node { public int data; public Node left, right; public Node(int item) { data = item; left = null; right = null; } } // Class to print Level Order Traversal public class BinaryTree { Node root; // Given a binary tree. Print // its nodes in level order using // array for implementing queue void printLevelOrder() { Queuekø = ny kø(); kø.Enqueue(rod); while (queue.Count != 0) { Node tempNode = queue.Dequeue(); Console.Write(tempNode.data + ' '); // Enqueue left child if (tempNode.left != null) { queue.Enqueue(tempNode.left); } // Enqueue right child if (tempNode.right != null) { queue.Enqueue(tempNode.right); } } } // Driverkode public static void Main() { // Oprettelse af et binært træ og indtastning af // noderne BinaryTree tree_level = new BinaryTree(); tree_level.root = ny node(1); tree_level.root.left = ny node(2); tree_level.root.right = ny node(3); tree_level.root.left.left = ny node(4); tree_level.root.left.right = ny node(5); Console.WriteLine('Niveaurækkefølgegennemgang ' + 'af binært træ er - '); tree_level.printLevelOrder(); } } // Denne kode bidraget af PrinciRaj1992> Javascript class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } // Class to represent a deque (double-ended queue) class Deque { constructor() { this.queue = []; } // Method to add an element to the end of the queue enqueue(item) { this.queue.push(item); } // Method to remove and return the first element of the queue dequeue() { return this.queue.shift(); } // Method to check if the queue is empty isEmpty() { return this.queue.length === 0; } } // Function to perform level order traversal of a binary tree function printLevelOrder(root) { // Create a deque to store nodes for traversal const queue = new Deque(); // Add the root node to the queue queue.enqueue(root); // Continue traversal until the queue is empty while (!queue.isEmpty()) { // Remove and get the first node from the queue const tempNode = queue.dequeue(); // Print the data of the current node console.log(tempNode.data + ' '); // Enqueue the left child if it exists if (tempNode.left !== null) { queue.enqueue(tempNode.left); } // Enqueue the right child if it exists if (tempNode.right !== null) { queue.enqueue(tempNode.right); } } } // Create a binary tree and enter the nodes const root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); // Print the level order traversal of the binary tree console.log('Level order traversal of binary tree is - '); printLevelOrder(root);> Produktion
Level Order traversal of binary tree is 1 2 3 4 5>
Tidskompleksitet: O(N) hvor N er antallet af noder i det binære træ.
Hjælpeplads: O(N) hvor N er antallet af noder i det binære træ.