Vi kender en træ er en ikke-lineær datastruktur. Det har ingen begrænsning på antallet af børn. ENHvad er et komplet binært træ?

Et komplet binært træ er en speciel type binært træ, hvor alle træets niveauer er fyldt fuldstændigt, undtagen de laveste niveau noder, som er udfyldt fra så venstre som muligt.

Komplet binært træ

Nogle terminologier for komplet binært træ:

• Rod – Node, hvor ingen kant kommer fra forælderen. Eksempel - node A
• Barn – Node, der har en indkommende kant, kaldes underordnet. Eksempel - knudepunkter B, F er underordnede af henholdsvis A og C.
• Søskende – Noder med samme forælder er søskende. Eksempel-D, E er søskende, da de har samme forælder B.
• Grad af en node – Antal børn af en bestemt forælder. Eksempel- Graden af ​​A er 2 og graden af ​​C er 1. Graden af ​​D er 0.
• Interne/Eksterne noder - Bladknuder er eksterne knuder, og ikke-bladknuder er interne knuder.
• Niveau – Tæl noder i en sti for at nå en destinationsknude. Eksempel- Niveau af knude D er 2, da knudepunkter A og B danner stien.
• Højde – Antal kanter for at nå destinationsknuden, Roden er i højden 0. Eksempel – Højden på knudepunktet E er 2, da den har to kanter fra roden.

Egenskaber for komplet binært træ:

• Et komplet binært træ siges at være et egentligt binært træ, hvor alle blade har samme dybde.
• I et komplet binært træ antal knudepunkter i dybden d er 2 ^d .
• I et komplet binært træ med n noder højden af ​​træet er log(n+1) .
• Alle niveauer undtagen det sidste niveau er helt fyldte.

Perfekt binært træ vs komplet binært træ:

Et binært træ med højden 'h' med det maksimale antal noder er a Perfekt binært træ.
For en given højde h , er det maksimale antal noder 2 ^h+1 -1 .

EN komplet binært træ i højden h er et perfekt binært træ op til højden h-1 , og i det sidste niveau er elementer gemt i venstre mod højre rækkefølge.

Eksempel 1:

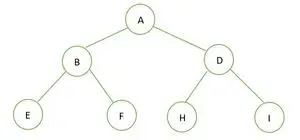
Et binært træ

Højden af ​​det givne binære træ er 2 og det maksimale antal knudepunkter i det træ er n=2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Derfor kan vi konkludere, at det er det et perfekt binært træ .
Nu for et komplet binært træ, det er fuldt op til højden h-1 dvs.; 1, og de sidste niveauelementer gemmes i venstre mod højre rækkefølge. Derfor er det også et komplet binært træ. Her er repræsentationen af ​​elementer, når de er gemt i et array

Element gemt i et array niveau for niveau

I arrayet gemmes alle elementer kontinuerligt.

Eksempel 2:

b+ træer

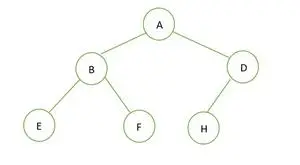
Et binært træ

Højden af ​​det givne binære træ er 2, og det maksimale antal noder, der bør være der, er 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Men antallet af noder i træet er 6 . Derfor er det ikke et perfekt binært træ .
Nu for et komplet binært træ, det er fuldt op til højden h-1 dvs.; 1 , og det sidste niveauelement gemmes i venstre mod højre rækkefølge. Derfor er dette en komplet binært træ . Gem elementet i et array, og det vil være som;

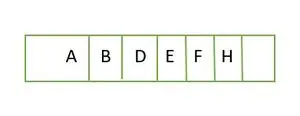
Element gemt i et array niveau for niveau

Eksempel 3:

java ende for loop

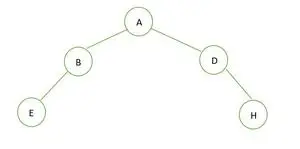
Et binært træ

Højden af ​​det binære træ er 2 og det maksimale antal noder, der kan være der, er 7, men der er kun 5 noder, derfor er det ikke et perfekt binært træ .
I tilfælde af et komplet binært træ, ser vi, at på det sidste niveau er elementer ikke udfyldt fra venstre mod højre rækkefølge. Sådan er det ikke et komplet binært træ .

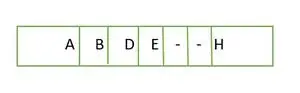
Element gemt i et array niveau for niveau

Elementerne i arrayet er ikke kontinuerlige.

Fuldt binært træ vs komplet binært træ:

For et fuldt binært træ har hver node enten 2 børn eller 0 børn.

Eksempel 1:

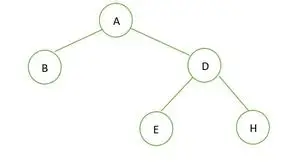
Et binært træ

I det givne binære træ er der ingen node med grad 1, enten 2 eller 0 børn for hver node, derfor er det et fuldt binært træ .

For et komplet binært træ gemmes elementer i niveau for niveau og ikke fra venstre side i det sidste niveau. Derfor er dette ikke et komplet binært træ . Array-repræsentationen er:

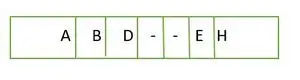
Element gemt i et array niveau for niveau

Eksempel 2:

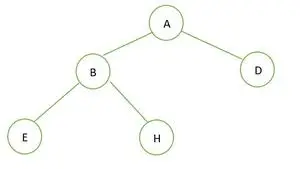
Et binært træ

I det givne binære træ er der ingen node med grad 1. Hver node har en grad på enten 2 eller 0. Derfor er det en fuldt binært træ .

For et komplet binært træ gemmes elementer på niveau for niveau og udfyldes fra den venstre side af det sidste niveau. Derfor denne a komplet binært træ . Nedenfor er array-repræsentationen af ​​træet:

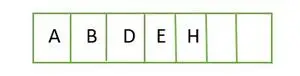
Element gemt i et array niveau for niveau

Eksempel 3:

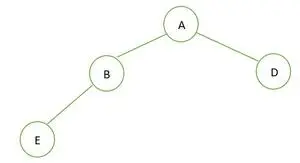
Et binært træ

I det givne binære træ har node B grad 1, hvilket krænker egenskaben af ​​fuldt binært træ, og derfor er det ikke et fuldt binært træ

strengfunktioner i java

For et komplet binært træ gemmes elementer i niveau for niveau og udfyldes fra den venstre side af det sidste niveau. Derfor er dette en komplet binært træ . Array repræsentation af det binære træ er:

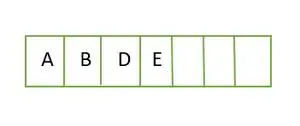
Element gemt i et array niveau for niveau

Eksempel 4:

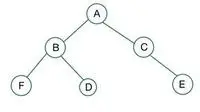
et binært træ

I det givne binære træ har node C grad 1, hvilket krænker egenskaben for et fuldt binært træ, og det er derfor ikke et fuldt binært træ

hashmap i java

For et komplet binært træ gemmes elementer i niveau for niveau og udfyldes fra den venstre side af det sidste niveau. Her overtræder node E betingelsen. Derfor er dette ikke et komplet binært træ .

Oprettelse af komplet binært træ:

Vi kender en komplet binært træ er et træ, hvor bortset fra det sidste niveau (f.eks l ) alle de andre niveauer har ( 2 l ) noder og noderne er linet op fra venstre mod højre side.
Det kan repræsenteres ved hjælp af et array. Hvis forælderen er det indeks jeg så venstre barn er kl 2i+1 og det rigtige barn er kl 2i+2 .

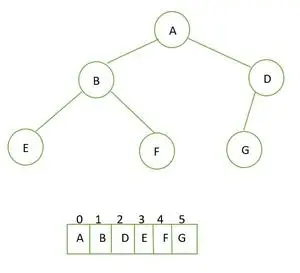
Komplet binært træ og dets matrixrepræsentation

Algoritme:

Til oprettelse af en Komplet binært træ , vi kræver en Trin 1: Initialiser roden med en ny node, når træet er tomt.

Trin 2: Hvis træet ikke er tomt, så få det forreste element

• Hvis det forreste element ikke har et venstre underordnet, så sæt det venstre underordnede til en ny node
• Hvis det rigtige barn ikke er til stede, indstil det rigtige barn som en ny node

Trin 3: Hvis noden har begge børn, så pop det fra køen.

Trin 4: Sæt de nye data i kø.

Illustration:

Overvej nedenstående array:

1. Det 1. element vil roden (værdi ved indeks = 0 )

sletning fra et binært søgetræ

A er taget som rod

2. Det næste element (ved indeks = 1 ) vil være venstre og tredje element (indeks = 2 ) vil være ret rodbarn

B som venstre barn og D som højre barn

3. fjerde (indeks = 3 ) og femte element (indeks = 4 ) vil være venstre og højre underordnede af B-knudepunktet

E og F er venstre og højre børn af B

4. Næste element (indeks = 5 ) vil efterlades underordnet af noden D

G er lavet til venstre barn af D-node

Sådan skabes et komplet binært træ.

Implementering: Til implementering af opbygning af et komplet binært træ fra niveauordregennemgang er givet i dette indlæg .

Anvendelse af det komplette binære træ:

• Dynge sortering
• Heap-sorteringsbaseret datastruktur

Tjek, om et givet binært træ er komplet eller ej: Følge efter dette indlæg for at kontrollere, om det givne binære træ er komplet eller ej.