Der er adskillige måder at evaluere en klassifikators ydeevne på. I denne artikel introducerer vi Precision-Recall Curve og undersøger yderligere forskellen mellem to populære præstationsrapporteringsmetoder: Precision-Recall (PR) Curve og Modtagerdriftskarakteristik (ROC) Kurve. ROC Curve er allerede diskuteret i artikel . Lad os kort forstå, hvad en Precision-Recall-kurve er.
Hvad er præcision og genkaldelse?
Præcision
- Forholdet mellem korrekt forudsagte positive observationer og alle forudsagte positive er kendt som præcision.
- Det måler, hvor godt modellen forudsiger de positive resultater.
- Præcisionsformlen er:
- Præcision handler om kvaliteten af positive forudsigelser. En høj præcision indikerer, at modellen har en lav rate af falske positiver.
Minde om
- Forholdet mellem korrekt forudsagte positive observationer og det samlede antal faktiske positive observationer er kendt som tilbagekaldelse.
- Det måler, hvor godt modellen kan fange hvert enkelt tilfælde.
- Tilbagekaldelse beregnes ved hjælp af denne formel:
- Tilbagekaldelse handler om mængden af de relevante tilfælde, der er fanget af modellen. En høj tilbagekaldelse indikerer, at modellen har en lav andel af falske negativer.
Med hensyn til empirisk fortolkning er en forvirringsmatrix bestående af fire væsentlige termer det mest nyttige værktøj til at forstå præcision og genkaldelse:
- True Positive (TP): Antallet af positive klasseforekomster, der er nøjagtigt identificeret
- Falsk positiv (FP): Antallet af negative klasseforekomster, der fejlagtigt identificeres som positive klasseforekomster, er kendt som falsk positive (FP).
- True Negative (TN): Antallet af negative klasseforekomster, der er nøjagtigt identificeret
- Falsk negativ (FN): Antal positive klasseforekomster, der fejlagtigt er klassificeret som negative klasseforekomster (falsk negativ eller FN)
Præcision-Recall (PR) kurve i maskinlæring
Præcision er andelen af korrekt positive klassifikationer (sandt positive) divideret med det samlede antal af forudsagt positive klassifikationer, der blev foretaget (sand positiv + falsk positiv). Minde om er andelen af korrekt positive klassifikationer (sandt positive) divideret med det samlede antal af de virkelig positive klassifikationer (sand positiv + falsk negativ).
En PR-kurve er simpelthen en graf med Præcisionsværdier på y-aksen og Recall-værdier på x-aksen. PR-kurven indeholder med andre ord
- Det er vigtigt at bemærke, at præcision også kaldes den positive prædiktive værdi (PPV).
- Tilbagekaldelsen kaldes også Sensitivity, Hit Rate eller True Positive Rate (TPR).
Figuren nedenfor viser en sammenligning af prøve-PR- og ROC-kurver. 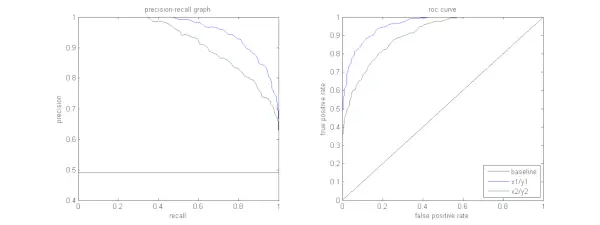
Fortolkning af en præcisions-genkaldelseskurve
Det ønskes, at algoritmen skal have både høj præcision og høj genkaldelse. De fleste maskinlæringsalgoritmer involverer dog ofte en afvejning mellem de to. En god PR-kurve har større AUC (areal under kurven) . I figuren ovenfor har klassificereren svarende til den blå linje bedre ydeevne end klassificereren svarende til den grønne linje. Det er vigtigt at bemærke, at klassificeringen, der har en højere AUC på ROC kurve vil altid også have en højere AUC på PR-kurven. Overvej en algoritme, der klassificerer, om et dokument tilhører kategorien Sportsnyheder eller ej. Antag, at der er 12 dokumenter med følgende grundsandhed (faktisk) og klassificeringsoutputklasseetiketter.
hvornår starter q2
| Dokument ID | Grund Sandhed | Klassificeringsudgang |
|---|---|---|
| D1 | Sport | Sport |
| D2 | Sport | Sport |
| D3 | Ikke sport | Sport |
| D4 | Sport | Ikke sport |
| D5 | Ikke sport | Ikke sport |
| D6 | Sport | Ikke sport |
| D7 | Ikke sport | Sport |
| D8 | Ikke sport | Ikke sport |
| D9 | Ikke sport | Ikke sport |
| D10 | Sport | Sport |
| D11 | Sport | Sport |
| D12 | Sport | Ikke sport |
Lad os nu finde TP-, TN-, FP- og FN-værdier.
Lad os bruge et eksempel, der involverer dokumenter, der er klassificeret som sport eller ikke sport, for bedre at forklare definitionerne af sande positive (TP), sande negative (TN), falske positive (FP) og falske negative (FN) i forbindelse med klassificering:
Sande positive (TP): Dokumenter, der præcist blev kategoriseret som Sport, og som i virkeligheden handlede om sport. Dokumenterne D1, D2, D10 og D11 i dette scenarie er forekomster af TP.
Sande negative (TN): True Negatives er de tilfælde, hvor dokumentet var passende mærket som Ikke sport, selvom det intet havde med sport at gøre. I dette tilfælde er TN demonstreret af dokumenterne D5, D8 og D9.
Falske positive (FP): Dokumenter, der fejlagtigt blev kategoriseret som sport, selvom de intet havde med sport at gøre. Her er nogle FP-eksempler, dokumenter D3 og D7.
Falske negativer (FN): Eksempler på dokumenter, der fejlagtigt blev stemplet som Ikke sport, men i virkeligheden handlede de om sport. Dokumenterne D4, D6 og D12 er i dette tilfælde FN-eksempler.
I betragtning af disse tal: By =4, TN =3, FP =2, FN =3
Endelig beregnes præcision og tilbagekaldelse som følger:
Precision = frac{TP}{TP+FP} = frac{4}{6} = frac{2}{3}
Recall = frac{TP}{TP+FN} = frac{4}{7} Det følger, at tilbagekaldelsen er 4/7, når præcisionen er 2/3. Sagt anderledes, af alle de tilfælde, der forventedes at være positive, var to tredjedele nøjagtigt klassificeret (præcision), og af alle de tilfælde, der faktisk var positive, var modellen i stand til at fange fire syvendedele af dem (genkaldelse).
skriv json til filen python
Ved at indstille forskellige tærskler får vi flere sådanne præcisionspar. Ved at plotte flere sådanne P-R-par med en af værdierne fra 0 til 1, får vi en PR-kurve.
Brug for en PR-kurve, når ROC-kurven eksisterer?
PR-kurve er især nyttig til rapportering af informationssøgningsresultater.
Informationssøgning involverer søgning i en pulje af dokumenter for at finde dem, der er relevante for en bestemt brugerforespørgsel. Antag for eksempel, at brugeren indtaster en søgeforespørgsel Pink Elephants. Søgemaskinen skimmer gennem millioner af dokumenter (ved hjælp af nogle optimerede algoritmer) for at hente en håndfuld relevante dokumenter. Derfor kan vi roligt antage, at nej. af relevante dokumenter vil være meget mindre i forhold til nr. af ikke-relevante dokumenter.
I dette scenarie,
- TP = Antal hentede dokumenter, der er relevante (gode resultater).
- FP = Antal hentede dokumenter, der er ikke-relevante (falske søgeresultater).
- TN = Antal ikke-hentede dokumenter, der er ikke-relevante.
- FN = Antal ikke-hentede dokumenter, der er relevante (gode dokumenter vi savnede).
ROC-kurven er et plot, der indeholder Recall = TPR =
Ydermere hjælper FPR os ikke med at evaluere et genfindingssystem godt, fordi vi ønsker at fokusere mere på de hentede dokumenter, og ikke de ikke-hentede. PR-kurve hjælper med at løse dette problem. PR-kurven har Recall-værdien (TPR) på x-aksen, og præcision =
Hvornår skal man bruge ROC vs. Precision-Recall Curves?
ROC (Receiver Operating Characteristic) kurver er velegnede, når klassefordelingen er afbalanceret, og falske positive og falske negative har lignende konsekvenser. De skildrer afvejningen mellem sensitivitet og specificitet. I modsætning hertil er Precision-Recall-kurver at foretrække, når man har at gøre med ubalancerede datasæt, med fokus på positiv klasseforudsigelsesydelse.
Precision-Recall giver indsigt i modellens evne til korrekt at klassificere positive tilfælde. Valget mellem ROC og Precision-Recall afhænger af problemets specifikke behov, hvilket understreger vigtigheden af at forstå datafordelingen og konsekvenserne af forskellige typer fejl.
Grundlæggende kodeimplementering til præcisions-genkaldelseskurve
Import af nødvendige biblioteker
Disse kodelinjer importerer Python biblioteker og moduler, der kræves til at generere en præcisions-genkaldelseskurve med sci-kit-learn og visualisere resultaterne med Matplotlib . Matplotlib er et populært Python-plotbibliotek, og pyplot giver en ligetil grænseflade til at skabe forskellige typer plot og diagrammer. Logistisk regression er en populær klassifikationsalgoritme til binære og multiklasse klassifikationsopgaver. Præcisions-genkaldelseskurven og AUC er populære evalueringsmålinger for binær klassifikation problemer, især ved håndtering af ubalancerede datasæt.
Python3 import matplotlib.pyplot as plt from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import precision_recall_curve, auc> Datasæt brugt
Denne kode genererer et syntetisk datasæt til et binært klassifikationsproblem ved hjælp af sci-kit-learns 'make_classification'-funktion.
Python3 # Generate a synthetic dataset X, y = make_classification( n_samples=1000, n_features=20, n_classes=2, random_state=42)> Træn og test split
Det train_test_split funktion i scikit-learn bruges i dette kodestykke til at opdele det tidligere genererede syntetiske datasæt (X og y) i trænings- og testsæt. Denne opdeling er et kritisk trin i evalueringen af maskinlæringsmodeller. Modellen vil blive trænet på X_train- og y_train-dataene, før den testes på X_test- og y_test-dataene for at se, hvor godt den klarer sig på usete prøver. Train_test_split-funktionen adskiller trænings- og testsæt og sikrer, at modellens ydeevne afspejler dens generalisering til nye, tidligere usete data.
Python3 # Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42)> Modelbygning
Her bruger vi logistisk regression til at træne modellen på træningsdatasættet. En populær algoritme til binær klassificering, logistisk regression er implementeret af sci-kit-learn-klassen LogisticRegression.
java-strengen indeholderPython3
# Train a logistic regression model (you can replace this with your own classifier) model = LogisticRegression() model.fit(X_train, y_train)> Model forudsigelse
Disse beregninger giver normalt præcisions- og genkaldelsesværdier for forskellige beslutningstærskler, som du kan bruge til at tegne en præcisions-genkaldelseskurve eller undersøge den relative betydning af præcision og genkald på forskellige tidspunkter. Og beregner Område under kurven (AUC) for præcisions-genkaldelseskurven.
Python3 # Predict probabilities for positive class y_scores = model.predict_proba(X_test)[:, 1] # Calculate precision and recall precision, recall, thresholds = precision_recall_curve(y_test, y_scores) # Calculate Area Under the Curve (AUC) for precision-recall curve auc_score = auc(recall, precision)> Plotte PR-kurve
Denne kodeblok giver en standardmetode til at visualisere præcisions-genkaldelseskurven og lader dig evaluere præcision kontra genkaldelse afvejning ved forskellige beslutningstærskler. Modellens overordnede ydeevne på præcisions-genkaldelseskurven er opsummeret af AUC-scoren vist i forklaringen.
Python3 # Plot precision-recall curve plt.figure(figsize=(8, 6)) plt.plot(recall, precision, label=f'Precision-Recall Curve (AUC = {auc_score:.2f})') plt.xlabel('Recall') plt.ylabel('Precision') plt.title('Precision-Recall Curve') plt.legend() plt.show()> Produktion :

Præcision-Recall Curve
Ofte stillede spørgsmål (FAQ)
Q. Hvad er præcision?
Forholdet mellem nøjagtigt forudsagte positive observationer og det samlede antal forudsagte positive er kendt som præcision. Det måler, hvor godt modellen forudsiger de positive resultater. Følgende er præcisionsformlen:
Precision = frac{True Positives}{True Positives + False Positives}
Q. Hvad er tilbagekaldelse?
Recall er forholdet mellem korrekt forudsagte positive observationer og det samlede antal faktiske positive. Det kaldes også følsomhed eller sand positiv rate. Den vurderer, hvor godt modellen kan fange hver enkelt relevant instans. Tilbagekaldelse beregnes ved hjælp af følgende formel:
Precision = frac{True Positives}{True Positives + False Negatives} vandmærke i word
Q. Hvorfor har vi brug for præcision og tilbagekaldelse?
For at vurdere en klassifikator ydeevne i binære og multiklasse klassifikationsproblemer, bruges to evalueringsmetrikker: præcision og tilbagekaldelse. Positiv forudsigelses nøjagtighed måles ved præcision, og positiv forudsigelses fuldstændighed måles ved tilbagekaldelse.
Sp. Hvad er afvejningen mellem tilbagekaldelse og præcision?
Genkaldelse og præcision er ofte afvejninger. Genkaldelse kan lide, når præcisionen stiger, og omvendt. Ved at ændre bjælken for at identificere en positiv instans kan denne afvejning styres. Omvendt resulterer en lavere tærskel i lavere genkald, men højere præcision. Beslutningen mellem tilbagekaldelse og præcision er baseret på detaljerne i det givne problem.
Q. Hvad er F1-score, og hvordan hænger det sammen med præcision og genkaldelse?
Det harmoniske middel for genkaldelse og præcision er kendt som F1-score. Det giver en retfærdig måling, der tager højde for både falske positive og falske negative. F1-score beregnes ved hjælp af følgende formel:
F1-Score = frac{2 imes Precision imes Recall}{Precision + Recall} F1-scoren er især nyttig, når præcision og genkaldelse er ude af balance, og en balance mellem de to er ønsket.
