Logistisk regression er en overvåget maskinlæringsalgoritme anvendes til klassifikationsopgaver hvor målet er at forudsige sandsynligheden for, at en instans tilhører en given klasse eller ej. Logistisk regression er en statistisk algoritme, der analyserer forholdet mellem to datafaktorer. Artiklen udforsker det grundlæggende i logistisk regression, dets typer og implementeringer.
Indholdsfortegnelse
- Hvad er logistisk regression?
- Logistisk funktion – Sigmoid funktion
- Typer af logistisk regression
- Antagelser om logistisk regression
- Hvordan fungerer logistisk regression?
- Kodeimplementering for logistisk regression
- Præcisions-tilbagekaldelse afvejning i logistisk regressionstærskelindstilling
- Hvordan evaluerer man logistisk regressionsmodel?
- Forskelle mellem lineær og logistisk regression
Hvad er logistisk regression?
Logistisk regression bruges til binær klassifikation hvor vi bruger sigmoid funktion , der tager input som uafhængige variable og producerer en sandsynlighedsværdi mellem 0 og 1.
For eksempel har vi to klasser Klasse 0 og Klasse 1, hvis værdien af den logistiske funktion for et input er større end 0,5 (tærskelværdi), så hører den til Klasse 1 ellers hører den til Klasse 0. Det kaldes regression, fordi det er en forlængelse af lineær regression men bruges hovedsageligt til klassifikationsproblemer.
hvilke måneder er q1
Centrale punkter:
- Logistisk regression forudsiger outputtet af en kategorisk afhængig variabel. Derfor skal resultatet være en kategorisk eller diskret værdi.
- Det kan enten være Ja eller Nej, 0 eller 1, sandt eller falsk osv., men i stedet for at give den nøjagtige værdi som 0 og 1, giver det de sandsynlige værdier, som ligger mellem 0 og 1.
- I logistisk regression tilpasser vi i stedet for at tilpasse en regressionslinje en S-formet logistisk funktion, som forudsiger to maksimale værdier (0 eller 1).
Logistisk funktion – Sigmoid funktion
- Sigmoid-funktionen er en matematisk funktion, der bruges til at kortlægge de forudsagte værdier til sandsynligheder.
- Den kortlægger enhver reel værdi til en anden værdi inden for et område på 0 og 1. Værdien af den logistiske regression skal være mellem 0 og 1, som ikke kan gå ud over denne grænse, så den danner en kurve ligesom S-formen.
- S-formkurven kaldes Sigmoid-funktionen eller logistikfunktionen.
- I logistisk regression bruger vi begrebet tærskelværdien, som definerer sandsynligheden for enten 0 eller 1. Som f.eks. værdier over tærskelværdien har en tendens til 1, og en værdi under tærskelværdierne har en tendens til 0.
Typer af logistisk regression
På baggrund af kategorierne kan logistisk regression klassificeres i tre typer:
- Binomial: I binomial logistisk regression kan der kun være to mulige typer af de afhængige variable, såsom 0 eller 1, Bestået eller Ikke bestået osv.
- Multinomial: I multinomial logistisk regression kan der være 3 eller flere mulige uordnede typer af den afhængige variabel, såsom kat, hunde eller får
- Ordinal: I ordinal logistisk regression kan der være 3 eller flere mulige sorterede typer af afhængige variabler, såsom lav, medium eller høj.
Antagelser om logistisk regression
Vi vil undersøge antagelserne om logistisk regression, da det er vigtigt at forstå disse antagelser for at sikre, at vi bruger passende anvendelse af modellen. Antagelsen omfatter:
- Uafhængige observationer: Hver observation er uafhængig af den anden. hvilket betyder, at der ikke er nogen sammenhæng mellem nogen inputvariable.
- Binære afhængige variabler: Det tager den antagelse, at den afhængige variabel skal være binær eller dikotom, hvilket betyder, at den kun kan tage to værdier. For mere end to kategorier bruges SoftMax-funktioner.
- Linearitetsforhold mellem uafhængige variable og log odds: Forholdet mellem de uafhængige variable og log odds for den afhængige variabel bør være lineær.
- Ingen outliers: Der bør ikke være nogen outliers i datasættet.
- Stor stikprøvestørrelse: Prøvestørrelsen er tilstrækkelig stor
Terminologier involveret i logistisk regression
Her er nogle almindelige udtryk involveret i logistisk regression:
- Uafhængige variabler: Inputkarakteristika eller prædiktorfaktorer anvendt på den afhængige variabels forudsigelser.
- Afhængig variabel: Målvariablen i en logistisk regressionsmodel, som vi forsøger at forudsige.
- Logistisk funktion: Formlen, der bruges til at repræsentere, hvordan de uafhængige og afhængige variabler relaterer til hinanden. Den logistiske funktion transformerer inputvariablerne til en sandsynlighedsværdi mellem 0 og 1, som repræsenterer sandsynligheden for, at den afhængige variabel er 1 eller 0.
- Odds: Det er forholdet mellem noget, der opstår, og noget, der ikke forekommer. det er forskelligt fra sandsynlighed, da sandsynligheden er forholdet mellem noget, der forekommer, og alt, hvad der kan forekomme.
- Log-odds: Log-odds, også kendt som logit-funktionen, er den naturlige logaritme af oddsene. Ved logistisk regression modelleres log odds for den afhængige variabel som en lineær kombination af de uafhængige variable og skæringspunktet.
- Koefficient: Den logistiske regressionsmodels estimerede parametre viser, hvordan de uafhængige og afhængige variabler relaterer til hinanden.
- Opsnappe: Et konstant led i den logistiske regressionsmodel, som repræsenterer log odds, når alle uafhængige variable er lig nul.
- Maksimal sandsynlighed estimering : Metoden, der bruges til at estimere koefficienterne for den logistiske regressionsmodel, som maksimerer sandsynligheden for at observere dataene givet modellen.
Hvordan fungerer logistisk regression?
Den logistiske regressionsmodel transformerer lineær regression funktion kontinuerlig værdi output til kategorisk værdi output ved hjælp af en sigmoid funktion, som kortlægger ethvert reelt værdisæt af uafhængige variable input til en værdi mellem 0 og 1. Denne funktion er kendt som den logistiske funktion.
Lad de uafhængige inputfunktioner være:
og den afhængige variabel er Y, der kun har binær værdi, dvs. 0 eller 1.
Anvend derefter den multi-lineære funktion på inputvariablerne X.
Her
uanset hvad vi diskuterede ovenfor er lineær regression .
Sigmoid funktion
Nu bruger vi sigmoid funktion hvor input vil være z og vi finder sandsynligheden mellem 0 og 1. dvs. forudsagt y.
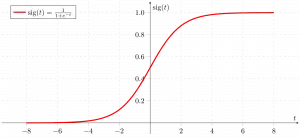
Sigmoid funktion
Som vist ovenfor konverterer figur sigmoid-funktionen de kontinuerlige variable data til sandsynlighed altså mellem 0 og 1.
sigma(z) tenderer mod 1 somz ightarrowinfty sigma(z) tenderer mod 0 somz ightarrow-infty sigma(z) er altid afgrænset mellem 0 og 1
hvor sandsynligheden for at være en klasse kan måles som:
Logistisk regressionsligning
Det ulige er forholdet mellem noget, der opstår, og noget, der ikke forekommer. det er forskelligt fra sandsynlighed, da sandsynligheden er forholdet mellem noget, der forekommer, og alt, hvad der kan forekomme. så mærkeligt vil være:
websteder som bedpage
Anvendelse af naturlig log på ulige. så vil log ulige være:
så vil den endelige logistiske regressionsligning være:
Sandsynlighedsfunktion for logistisk regression
De forudsagte sandsynligheder vil være:
- for y=1 De forudsagte sandsynligheder vil være: p(X;b,w) = p(x)
- for y = 0 De forudsagte sandsynligheder vil være: 1-p(X;b,w) = 1-p(x)
Tager naturlige træstammer på begge sider
Gradient af log-sandsynlighedsfunktionen
For at finde de maksimale sandsynlighedsestimater differentierer vi w.r.t.
Kodeimplementering for logistisk regression
Binomial logistisk regression:
Målvariabel kan kun have 2 mulige typer: 0 eller 1, som kan repræsentere sejr vs tab, bestået vs mislykket, død vs levende osv., i dette tilfælde bruges sigmoid-funktioner, hvilket allerede er diskuteret ovenfor.
Import af nødvendige biblioteker baseret på kravet om model. Denne Python-kode viser, hvordan man bruger brystkræftdatasættet til at implementere en logistisk regressionsmodel til klassificering.
Python3 # import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X, y = load_breast_cancer(return_X_y=True) # split the train and test dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23) # LogisticRegression clf = LogisticRegression(random_state=0) clf.fit(X_train, y_train) # Prediction y_pred = clf.predict(X_test) acc = accuracy_score(y_test, y_pred) print('Logistic Regression model accuracy (in %):', acc*100)> Produktion :
Logistisk regressionsmodels nøjagtighed (i %): 95,6140350877193
Multinomiel logistisk regression:
Målvariabel kan have 3 eller flere mulige typer, som ikke er ordnet (dvs. typer har ingen kvantitativ betydning) som sygdom A vs sygdom B vs sygdom C.
I dette tilfælde bruges softmax-funktionen i stedet for sigmoid-funktionen. Softmax funktion for K klasser vil være:
Her, K repræsenterer antallet af elementer i vektoren z, og i, j itererer over alle elementerne i vektoren.
Så vil sandsynligheden for klasse c være:
I Multinomial Logistic Regression kan outputvariablen have mere end to mulige diskrete udgange . Overvej cifferdatasættet.
Python3 from sklearn.model_selection import train_test_split from sklearn import datasets, linear_model, metrics # load the digit dataset digits = datasets.load_digits() # defining feature matrix(X) and response vector(y) X = digits.data y = digits.target # splitting X and y into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) # create logistic regression object reg = linear_model.LogisticRegression() # train the model using the training sets reg.fit(X_train, y_train) # making predictions on the testing set y_pred = reg.predict(X_test) # comparing actual response values (y_test) # with predicted response values (y_pred) print('Logistic Regression model accuracy(in %):', metrics.accuracy_score(y_test, y_pred)*100)> Produktion:
java liste metoder
Logistisk regressionsmodels nøjagtighed (i %): 96,52294853963839
Hvordan evaluerer man logistisk regressionsmodel?
Vi kan evaluere den logistiske regressionsmodel ved hjælp af følgende metrics:
- Nøjagtighed: Nøjagtighed angiver andelen af korrekt klassificerede tilfælde.
Accuracy = frac{True , Positives + True , Negatives}{Total}
- Præcision: Præcision fokuserer på nøjagtigheden af positive forudsigelser.
Precision = frac{True , Positives }{True, Positives + False , Positives}
- Genkaldelse (følsomhed eller sand positiv rate): Minde om måler andelen af korrekt forudsagte positive tilfælde blandt alle faktiske positive tilfælde.
Recall = frac{ True , Positives}{True, Positives + False , Negatives}
- F1-score: F1 score er det harmoniske middel af præcision og genkaldelse.
F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}
- Område under modtagerens driftskarakteristikkurve (AUC-ROC): ROC-kurven plotter den sande positive rate mod den falske positive rate ved forskellige tærskler. AUC-ROC måler arealet under denne kurve og giver et samlet mål for en models ydeevne på tværs af forskellige klassifikationstærskler.
- Area Under the Precision-Recall Curve (AUC-PR): Svarende til AUC-ROC, AUC-PR måler området under præcisions-genkaldelseskurven, hvilket giver en oversigt over en models ydeevne på tværs af forskellige præcisions-genkaldelse-afvejninger.
Præcisions-tilbagekaldelse afvejning i logistisk regressionstærskelindstilling
Logistisk regression bliver først en klassifikationsteknik, når en beslutningstærskel bringes ind i billedet. Indstillingen af tærskelværdien er et meget vigtigt aspekt af logistisk regression og afhænger af selve klassifikationsproblemet.
Beslutningen om værdien af tærskelværdien er i høj grad påvirket af værdierne på præcision og genkaldelse. Ideelt set ønsker vi, at både præcision og tilbagekaldelse er 1, men det er sjældent tilfældet.
I tilfælde af en Afvejning mellem præcision og tilbagekaldelse , bruger vi følgende argumenter til at bestemme tærsklen:
- Lav præcision/høj genkaldelse: I applikationer, hvor vi ønsker at reducere antallet af falske negativer uden nødvendigvis at reducere antallet af falske positive, vælger vi en beslutningsværdi, der har en lav værdi på Præcision eller en høj værdi på Genkald. For eksempel ønsker vi i en ansøgning om kræftdiagnose ikke, at nogen berørt patient skal klassificeres som ikke berørt uden at være meget opmærksom på, hvis patienten fejlagtigt bliver diagnosticeret med kræft. Dette skyldes, at fraværet af kræft kan påvises af yderligere medicinske sygdomme, men tilstedeværelsen af sygdommen kan ikke påvises hos en allerede afvist kandidat.
- Høj præcision/lav genkaldelse: I applikationer, hvor vi ønsker at reducere antallet af falske positiver uden nødvendigvis at reducere antallet af falske negativer, vælger vi en beslutningsværdi, der har en høj værdi på Præcision eller en lav værdi på Recall. Hvis vi for eksempel klassificerer kunder, om de vil reagere positivt eller negativt på en personlig annonce, vil vi være helt sikre på, at kunden vil reagere positivt på annoncen, da en negativ reaktion ellers kan medføre et tab af potentielt salg fra kunde.
Forskelle mellem lineær og logistisk regression
Forskellen mellem lineær regression og logistisk regression er, at lineær regressionsoutput er den kontinuerlige værdi, der kan være hvad som helst, mens logistisk regression forudsiger sandsynligheden for, at en instans tilhører en given klasse eller ej.
Lineær regression | Logistisk regression |
|---|---|
Lineær regression bruges til at forudsige den kontinuerlige afhængige variabel ved hjælp af et givet sæt af uafhængige variable. | Logistisk regression bruges til at forudsige den kategoriske afhængige variabel ved hjælp af et givet sæt af uafhængige variable. |
Lineær regression bruges til at løse regressionsproblem. | Det bruges til at løse klassifikationsproblemer. |
I denne forudsiger vi værdien af kontinuerte variable | I dette forudsiger vi værdier af kategoriske variable |
I denne finder vi den bedste pasform linje. | I denne finder vi S-Kurve. |
Mindste kvadratisk estimeringsmetode bruges til estimering af nøjagtighed. | Maksimal sandsynlighed estimering metode bruges til estimering af nøjagtighed. |
Outputtet skal være kontinuerlig værdi, såsom pris, alder osv. | Output skal være kategorisk værdi såsom 0 eller 1, Ja eller nej osv. |
Det krævede lineær sammenhæng mellem afhængige og uafhængige variable. | Det krævede ikke lineært forhold. instansiering i java |
Der kan være kolinearitet mellem de uafhængige variable. | Der bør ikke være kolinearitet mellem uafhængige variable. |
Logistisk regression – ofte stillede spørgsmål (FAQ)
Hvad er logistisk regression i maskinlæring?
Logistisk regression er en statistisk metode til udvikling af maskinlæringsmodeller med binære afhængige variabler, altså binære. Logistisk regression er en statistisk teknik, der bruges til at beskrive data og forholdet mellem en afhængig variabel og en eller flere uafhængige variable.
Hvad er de tre typer af logistisk regression?
Logistisk regression er klassificeret i tre typer: binær, multinomial og ordinal. De adskiller sig både i udførelse og teori. Binær regression handler om to mulige udfald: ja eller nej. Multinomial logistisk regression bruges, når der er tre eller flere værdier.
Hvorfor logistisk regression bruges til klassificeringsproblem?
Logistisk regression er lettere at implementere, fortolke og træne. Det klassificerer ukendte poster meget hurtigt. Når datasættet er lineært adskilleligt, fungerer det godt. Modelkoefficienter kan fortolkes som indikatorer for karakteristika.
Hvad adskiller logistisk regression fra lineær regression?
Mens lineær regression bruges til at forudsige kontinuerlige resultater, bruges logistisk regression til at forudsige sandsynligheden for, at en observation falder ind under en bestemt kategori. Logistisk regression anvender en S-formet logistisk funktion til at kortlægge forudsagte værdier mellem 0 og 1.
Hvilken rolle spiller den logistiske funktion i logistisk regression?
Logistisk regression er afhængig af den logistiske funktion til at konvertere output til en sandsynlighedsscore. Denne score repræsenterer sandsynligheden for, at en observation tilhører en bestemt klasse. Den S-formede kurve hjælper med tærskelværdi og kategorisering af data i binære resultater.
