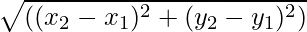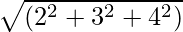logo

TechCodeview

Størrelsen af ​​en vektor

Vektormængder er de mængder, der har både retning og størrelse. Størrelsen af ​​en vektor er længden af ​​vektoren. Den er givet ved den numeriske værdi af vektoren, og da den repræsenterer længden af ​​vektoren, er den altid positiv. For enhver vektor 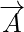overrightarrow{A}dens størrelse er repræsenteret som overrightarrow{A}.

Lad os lære mere om størrelsen af ​​vektoren dens formel, eksempler og andet i denne artikel.



Indholdsfortegnelse

Hvad er størrelsen af ​​en vektor?

Størrelsen af ​​en vektor er defineret som længden af ​​vektoren. Da størrelsen af ​​vektoren angiver længden af ​​vektoren, er den altid positiv. For enhver vektor A er dens størrelse repræsenteret som |A|. Antag, at en vektor er defineret som xi + yj, så er dens størrelse defineret som kvadratroden af ​​summen af ​​kvadraterne af de enkelte led. Størrelsen af ​​vektoren repræsenterer længden af ​​vektoren, dvs. den værdi eller påvirkning vektoren har.

For eksempel, hvis en kraft på 5i N virker på en genstand, er dens størrelse 5 N, hvilket betyder, at styrken af ​​den påførte kraft er 5 N, og ' jeg' i 5i repræsenterer, at den anvendes i den positive x-retning.



Størrelsen af ​​en vektorformel

Der er forskellige måder at beregne størrelsen af ​​vektoren på. Baseret på de givne data, brug en anden form for formel til at finde størrelsen af ​​en vektor. Størrelsen af ​​en vektor A er repræsenteret ved hjælp af modulusoperatoren, dvs. |A|

Der er forskellige formler, der bruges til at tælle størrelsen af ​​vektoren. Følgende billede viser de vigtige formler, der bruges til at finde størrelsen af ​​vektoren.

Størrelsen af ​​en vektorformel

Følgende er måderne at beregne størrelsen på.



  • Hvis de får en vektor Ā = xi+ yĵ + zk̂, kan størrelsen af ​​vektor Ā beregnes ved hjælp af nedenstående formel

Størrelsen af ​​vektor Ā (|A|) = √(x 2 + og 2 +z 2 )

  • Hvis startpunktsvektoren er sig (x1, og1) og endepunktet for en vektor er sige (x2, og2) gives derefter størrelsen af ​​vektoren overrightarrow{AB}er givet af,
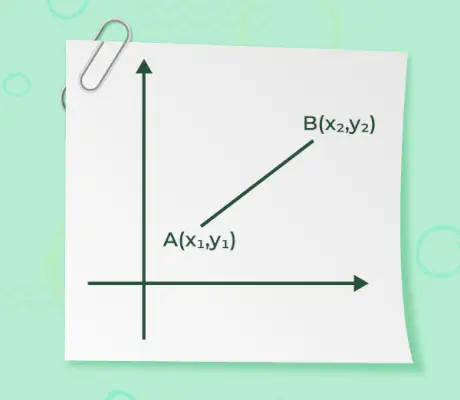
Størrelsen af ​​vektoren, hvis der er givet to punkter

Størrelsen af ​​en vektor, når start- og slutpunkterne for en vektor er givet, er intet andet end afstanden mellem punkterne. Formlen for at finde størrelse er givet ved

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Hvis noget af start- eller slutpunkterne for en vektor er ved origo o(0, 0), og et andet punkt er A(x, y) som angivet i nedenstående figur,
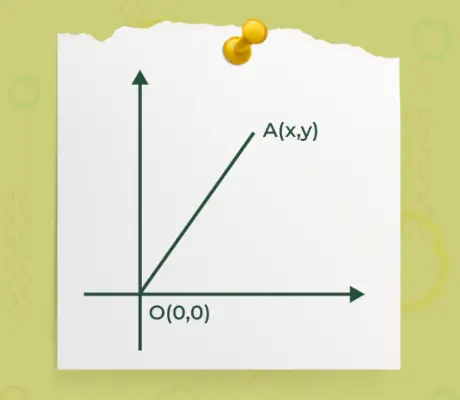
Vektorens størrelse, hvis der er givet ét punkt og oprindelse

Så er formlen for at finde størrelsen af ​​en vektor, hvor en af ​​enderne af en vektor er ved origo givet ved

|Ā| = √(x 2 +y 2 )

Retning af en vektor

Vektormængder er mængder, der har både størrelser og retninger. Retningen af ​​vektormængden angiver i hvilken retning vektormængden anvendes. Det er defineret som den vinkel, som vektoren laver med den vandrette linje eller x-aksen. Det er repræsenteret ved symbolet -en .

Billedet nedenfor viser pilen, som bruges til at vise vektorens retning.

Vektorens retning

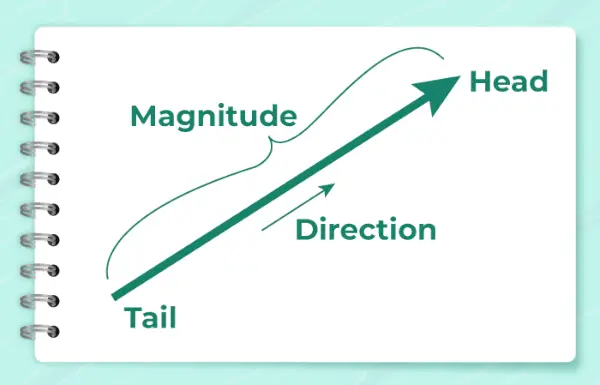
Det beregnes ved hjælp af formlen,

α = tan -1 (y/x)

boolesk til streng java

For vektoren genereret af koordinaterne (x1, og1) og (x2, og2) deres retning er givet af formlen,

α = tan -1 [(og 2 - og 1 )/(x 2 - x 1 )]

Hvordan finder man størrelsen af ​​en vektor?

Størrelsen af ​​vektoren beregnes ved hjælp af trinene beskrevet nedenfor,

Trin 1: Identificer x-, y- og z-komponenterne i vektoren.

Trin 2 : Find kvadratet af alle x-, y- og z-komponenterne.

Trin 3: Tilføj alle firkanterne fundet i trin 2.

Trin 4: Find kvadratroden af ​​summen opnået i trin 3.

Værdien opnået efter trin 4 er størrelsen af ​​den givne vektor.

Eksempel: Find størrelsen af ​​vektoren A = 3i + 4j

liste sortering java

Løsning:

Størrelsen af ​​vektor A beregnes ved hjælp af trinene beskrevet ovenfor.

Trin 1: Ved at sammenligne A = 3i + 4j med xi + yj får vi x = 3 og y = 4

Trin 2: x2= 32= 9 og y2= 42= 16

Trin 3: x2+ og2= 9 + 16 = 25

Trin 4: √(25) = 5

Således er størrelsen af ​​vektoren A = 3i + 4j 5 enheder.

Konklusion

Afslutningsvis fortæller størrelsen af ​​en vektor os, hvor lang vektoren er. Dette koncept er meget vigtigt på mange områder som fysik, teknik og datalogi, fordi det hjælper med at måle ting som hastighed, kraft og bevægelsesretning. Ved at forstå vektorstørrelsen kan vi bedre analysere og løse praktiske problemer, hvilket gør det til et vigtigt stykke viden for alle, der arbejder med tal og målinger i applikationer fra den virkelige verden.

Læs mere,

Løste eksempler på vektorstørrelse

Eksempel 1: Find størrelsen for vektoren Ā = 2i + 3ĵ + 4k.

Løsning:

streng til heltal java

givet,

Ā = 2i + 3ĵ + 4k

Størrelse |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Størrelsen af ​​vektor 2i+3ĵ+4k er 5,38 enhed

Eksempel 2: Find størrelsen for vektoren Ā = 3i + 3ĵ – 6k

Løsning:

Givet

Ā = 3i + 3ĵ – 6k

Størrelse |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Størrelsen af ​​vektor 3i+ 3ĵ – 6k er 7,35 enhed.

Eksempel 3: Find størrelsen af ​​vektoren, hvis startpunktet for en vektor er (3, 4) og slutpunktet er (6, 2).

Løsning:

givet,

(x1, og1) = (3, 4)
(x2, og2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Således er størrelsen af ​​den givne vektor 3.6 enhed.

Eksempel 4: Find størrelsen af ​​vektoren, hvis startpunktet for en vektor er (2, 1, 4) og slutpunktet er (5, 2, 6).

Løsning:

givet,

(x1, og1, Med1) = (2, 1, 4)

(x2, og2, Med2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Således er størrelsen af ​​den givne vektor 3,74 enhed.

Eksempel 5: Hvad er størrelsen af ​​vektoren, som starter ved origo og endepunkt ved (3, 4).

Løsning:

givet,

Vektorens startpunkt er O(0, 0)

første ordens logik

Slutpunkt (x, y) = (3, 4)

Størrelsen af ​​vektor (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Således er størrelsen af ​​den givne vektor 5 enhed.

Eksempel 6: Find størrelsen af ​​vektoren, hvor et af endepunkterne er ved origo og det andet punkt ved (1, 4, 3).

Løsning:

givet,

Vektorens slutpunkt er O(0, 0)

Andet punkt (x, y, z) = (1, 4, 3)

Størrelsen af ​​vektor (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Således er størrelsen af ​​den givne vektor 5,09 enhed.

foreach loop typescript

Ofte stillede spørgsmål om størrelsen af ​​en vektor

Hvad er størrelsen af ​​en vektorformel?

Størrelsen af ​​en vektor er den numeriske værdi af vektoren, og den definerer længden af ​​vektoren. For enhver vektor er A dens størrelse repræsenteret som |A|. Størrelsen af ​​vektoren beregnes ved hjælp af formlen,

For enhver vektor er A = xi + yj + zk dens størrelse givet af formlen

|A| = √(x 2 + og 2 + z 2 )

For enhver vektor, hvis startpunkt og slutpunkt er henholdsvis (x1, og1) og (x2, og2) dens størrelse er givet af formlen

|A| = √((x 2 - x 1 ) 2 + (og 2 - og 1 ) 2 )

Hvordan repræsenterer man størrelsen af ​​en vektor?

Størrelsen af ​​vektoren EN er repræsenteret ved symbolet |A|.

Hvordan finder man størrelsen af ​​en vektor?

Forskellige formler bruges til at beregne størrelsen af ​​vektoren, nogle af dem er,

  • |A| = √(x 2 + og 2 + z 2 ) når vektoren er i form af A = xi + yj + zk
  • |A| = √((x) 2 + (og) 2 ) når vektoren er givet ved punkt A (x, y) og origo O(0, 0).
  • |A| = √((x 2 - x 1 ) 2 + (og 2 - og 1 ) 2 ) når vektoren er givet af punkt A (x1, og2) og punkt B (x2, og2).

Find en vektor med størrelsesorden 5.

Der er forskellige vektorer, som kan have en størrelsesorden på 5, hvoraf et eksempel er vektor A repræsenteret som,

A = 3i + 4j Eller A = 4i + 5j