Logistisk regression i R-programmering er en klassifikationsalgoritme, der bruges til at finde sandsynligheden for begivenhedssucces og begivenhedsfejl. Logistisk regression bruges, når den afhængige variabel er binær (0/1, Sand/Falsk, Ja/Nej) i naturen. Logit-funktionen bruges som en linkfunktion i en binomialfordeling.
En binær udfaldsvariabels sandsynlighed kan forudsiges ved hjælp af den statistiske modelleringsteknik kendt som logistisk regression. Det er bredt ansat i mange forskellige brancher, herunder marketing, finans, samfundsvidenskab og medicinsk forskning.
Den logistiske funktion, almindeligvis omtalt som sigmoid-funktionen, er den grundlæggende idé, der understøtter logistisk regression. Denne sigmoid-funktion bruges i logistisk regression til at beskrive korrelationen mellem prædiktorvariablerne og sandsynligheden for det binære udfald.

Logistisk regression i R-programmering
Logistisk regression er også kendt som Binomial logistisk regression . Den er baseret på sigmoid-funktionen, hvor output er sandsynlighed, og input kan være fra -uendeligt til +uendeligt.
Teori
Logistisk regression er også kendt som en generaliseret lineær model. Da det bruges som en klassifikationsteknik til at forudsige en kvalitativ respons, varierer værdien af y fra 0 til 1 og kan repræsenteres af følgende ligning:

Logistisk regression i R-programmering
s er sandsynligheden for karakteristik af interesse. Oddsforholdet er defineret som sandsynligheden for succes i forhold til sandsynligheden for fiasko. Det er en nøglerepræsentation af logistiske regressionskoefficienter og kan tage værdier mellem 0 og uendelig. Oddsforholdet 1 er, når sandsynligheden for succes er lig med sandsynligheden for fiasko. Oddsforholdet 2 er, når sandsynligheden for succes er dobbelt så stor som sandsynligheden for fiasko. Oddsforholdet på 0,5 er, når sandsynligheden for fiasko er dobbelt så stor som sandsynligheden for succes.
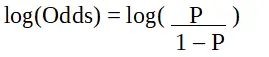
Logistisk regression i R-programmering
Da vi arbejder med en binomialfordeling (afhængig variabel), skal vi vælge en linkfunktion, der er bedst egnet til denne fordeling.
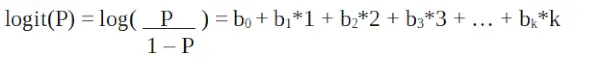
Logistisk regression i R-programmering
Det er en logit funktion . I ligningen ovenfor er parentesen valgt for at maksimere sandsynligheden for at observere stikprøveværdierne i stedet for at minimere summen af kvadratiske fejl (som almindelig regression). Logitten er også kendt som en log over odds. Logit-funktionen skal være lineært relateret til de uafhængige variable. Dette er fra ligning A, hvor venstre side er en lineær kombination af x. Dette svarer til OLS-antagelsen om, at y er lineært relateret til x. Variabler b0, b1, b2 … osv. er ukendte og skal estimeres på tilgængelige træningsdata. I en logistisk regressionsmodel ændres logit med b0 ved at gange b1 med én enhed. P-ændringerne på grund af en ændring på én enhed vil afhænge af værdien ganget. Hvis b1 er positiv, vil P stige, og hvis b1 er negativ, vil P falde.
Datasættet
mtcars (motortrend bilvejtest) omfatter brændstofforbrug, ydeevne og 10 aspekter af bildesign for 32 biler. Den leveres forudinstalleret med dplyr pakke i R.
R
# Installing the package> install.packages>(>'dplyr'>)> # Loading package> library>(dplyr)> # Summary of dataset in package> summary>(mtcars)> |
>
>
Udførelse af logistisk regression på et datasæt
Logistisk regression implementeres i R vha glm() ved at træne modellen ved hjælp af funktioner eller variable i datasættet.
R
# Installing the package> # For Logistic regression> install.packages>(>'caTools'>)> # For ROC curve to evaluate model> install.packages>(>'ROCR'>)> > # Loading package> library>(caTools)> library>(ROCR)> |
>
>
Opdeling af data
R
# Splitting dataset> split <->sample.split>(mtcars, SplitRatio = 0.8)> split> train_reg <->subset>(mtcars, split ==>'TRUE'>)> test_reg <->subset>(mtcars, split ==>'FALSE'>)> # Training model> logistic_model <->glm>(vs ~ wt + disp,> >data = train_reg,> >family =>'binomial'>)> logistic_model> # Summary> summary>(logistic_model)> |
>
>
Produktion:
Call: glm(formula = vs ~ wt + disp, family = 'binomial', data = train_reg) Deviance Residuals: Min 1Q Median 3Q Max -1.6552 -0.4051 0.4446 0.6180 1.9191 Coefficients: Estimate Std. Error z value Pr(>|z|) (Skæring) 1,58781 2,60087 0,610 0,5415 vægt 1,36958 1,60524 0,853 0,3936 disp -0,02969 0,01577 -1,898 0,0577 -1,898 0. --- Signif. koder: 0 '***' 0,001 '**' 0,01 '*' 0,05 '.' 0,1 ' ' 1 (Spredningsparameter for binomial familie taget til at være 1) Nul afvigelse: 34,617 på 24 frihedsgrader Restafvigelse: 20,212 på 22 frihedsgrader AIC: 26.212 Antal Fisher Scoring iterationer: 6>
- Kald: Funktionskaldet, der bruges til at passe til den logistiske regressionsmodel, vises sammen med oplysninger om familie, formel og data. Afvigelsesrester: Disse er afvigelsesresterne, som måler modellens grad af god pasform. De står for uoverensstemmelser mellem faktiske svar og sandsynlighed forudsagt af den logistiske regressionsmodel. Koefficienter: Disse koefficienter i logistisk regression repræsenterer svarvariablens log odds eller logit. Standardfejlene relateret til de estimerede koefficienter er vist i Std. Fejl kolonne. Signifikanskoder: Signifikansniveauet for hver prædiktorvariabel er angivet med signifikanskoderne. Spredningsparameter: Ved logistisk regression fungerer spredningsparameteren som skaleringsparameter for binomialfordelingen. Den er sat til 1 i dette tilfælde, hvilket indikerer, at den forudsatte spredning er 1. Nul afvigelse: Nul afvigelsen beregner modellens afvigelse, når blot skæringspunktet tages i betragtning. Det symboliserer den afvigelse, der ville følge af en model uden forudsigelser. Residual afvigelse: Residual afvigelsen beregner modellens afvigelse efter at prædiktorerne er blevet tilpasset. Det står for den resterende afvigelse efter at have taget højde for prædiktorerne. AIC: Akaike Information Criterion (AIC), som tegner sig for antallet af prædiktorer, er en målestok for en models god pasform. Det straffer mere indviklede modeller for at forhindre overfitting. Bedre passende modeller er angivet med lavere AIC-værdier. Antal Fisher Scoring-iterationer: Antallet af iterationer, der kræves af Fisher-scoringproceduren for at estimere modelparametrene, er angivet ved antallet af iterationer.
Forudsig testdata baseret på model
R
predict_reg <->predict>(logistic_model,> >test_reg, type =>'response'>)> predict_reg> |
>
>
Produktion:
Hornet Sportabout Merc 280C Merc 450SE Chrysler Imperial 0.01226166 0.78972164 0.26380531 0.01544309 AMC Javelin Camaro Z28 Ford Pantera L 0.06104267 0.02807992 0.01107943>
R
# Changing probabilities> predict_reg <->ifelse>(predict_reg>0,5, 1, 0)> # Evaluating model accuracy> # using confusion matrix> table>(test_reg$vs, predict_reg)> missing_classerr <->mean>(predict_reg != test_reg$vs)> print>(>paste>(>'Accuracy ='>, 1 - missing_classerr))> # ROC-AUC Curve> ROCPred <->prediction>(predict_reg, test_reg$vs)> ROCPer <->performance>(ROCPred, measure =>'tpr'>,> >x.measure =>'fpr'>)> auc <->performance>(ROCPred, measure =>'auc'>)> auc <- [email protected][[1]]> auc> # Plotting curve> plot>(ROCPer)> plot>(ROCPer, colorize =>TRUE>,> >print.cutoffs.at =>seq>(0.1, by = 0.1),> >main =>'ROC CURVE'>)> abline>(a = 0, b = 1)> auc <->round>(auc, 4)> legend>(.6, .4, auc, title =>'AUC'>, cex = 1)> |
>
>
Produktion:
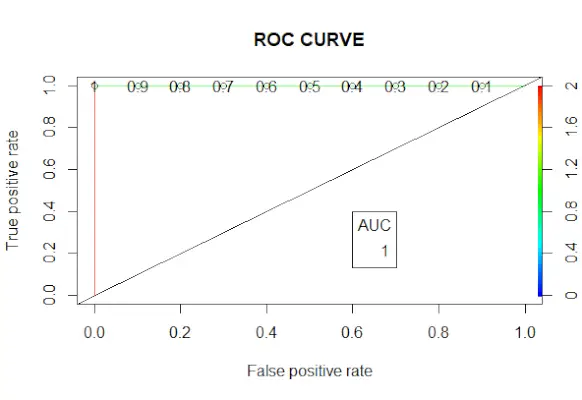
ROC-kurve
Eksempel 2:
Vi kan udføre en logistisk regressionsmodel Titanic Datasæt i R.
R
js global variabel
# Load the dataset> data>(Titanic)> # Convert the table to a data frame> data <->as.data.frame>(Titanic)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # View the summary of the model> summary>(model)> |
>
>
Produktion:
Call: glm(formula = Survived ~ Class + Sex + Age, family = binomial, data = data) Deviance Residuals: Min 1Q Median 3Q Max -1.177 -1.177 0.000 1.177 1.177 Coefficients: Estimate Std. Error z value Pr(>|z|) (Afskæring) 4.022e-16 8.660e-01 0 1 Class2nd -9.762e-16 1.000e+00 0 1 Class3rd -4.699e-16 1.000e+00 0 1 ClassCrew -5.611e. 00 0 1 KønKvinde -3.140e-16 7.071e-01 0 1 AlderVoksen 5.103e-16 7.071e-01 0 1 (Spredningsparameter for binomial familie taget til at være 1) Nulafvigelse: 44.361 af frihedsgrad 31. frihedsgrad: 14grader Rest. på 26 frihedsgrader AIC: 56.361 Antal Fisher Scoring iterationer: 2>
Plot ROC-kurven for Titanic-datasættet
R
# Install and load the required packages> install.packages>(>'ROCR'>)> library>(ROCR)> # Fit the logistic regression model> model <->glm>(Survived ~ Class + Sex + Age, family = binomial, data = data)> # Make predictions on the dataset> predictions <->predict>(model, type =>'response'>)> # Create a prediction object for ROCR> prediction_objects <->prediction>(predictions, titanic_df$Survived)> # Create an ROC curve object> roc_object <->performance>(prediction_obj, measure =>'tpr'>, x.measure =>'fpr'>)> # Plot the ROC curve> plot>(roc_object, main =>'ROC Curve'>, col =>'blue'>, lwd = 2)> # Add labels and a legend to the plot> legend>(>'bottomright'>, legend => >paste>(>'AUC ='>,>round>(>performance>(prediction_objects, measure =>'auc'>)> >@y.values[[1]], 2)), col =>'blue'>, lwd = 2)> |
>
>
Produktion:
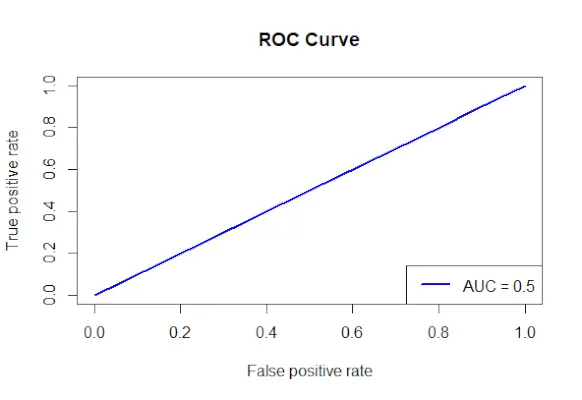
ROC kurve
- Faktorerne, der bruges til at forudsige overlevet, er specificeret, og formlen overlevet klasse + køn + alder bruges til at skabe en logistisk regressionsmodel.
- Ved hjælp af predict()-funktionen laves forudsigelser på datasættet ved hjælp af den tilpassede model.
- De projicerede sandsynligheder kombineres med de faktiske udfaldsværdier for at bygge et forudsigelsesobjekt ved hjælp af prædiction()-metoden fra ROCR-pakken.
- Målingen af den sande positive rate (tpr) og x-aksen for den falske positive rate (fpr) er specificeret, og et ROC-kurveobjekt oprettes ved hjælp af funktionen performance() fra ROCR-pakken.
- ROC-kurveobjektet (roc_obj), som angiver hovedtitlen, farven og linjebredden, plottes ved hjælp af plot()-funktionen.
- Den bruger funktionen performance() med måle = auc til at bestemme AUC-værdien (areal under kurven) og tilføjer etiketter og en forklaring til plottet.
