Begrænsningerne ved traditionelle binære søgetræer kan være frustrerende. Mød B-Tree, den multitalenterede datastruktur, der nemt kan håndtere enorme mængder data. Når det kommer til lagring og søgning i store mængder data, kan traditionelle binære søgetræer blive upraktiske på grund af deres dårlige ydeevne og høje hukommelsesforbrug. B-Trees, også kendt som B-Tree eller Balanced Tree, er en type selvbalancerende træ, der er specielt designet til at overvinde disse begrænsninger.
I modsætning til traditionelle binære søgetræer er B-Trees kendetegnet ved det store antal nøgler, som de kan gemme i en enkelt node, hvorfor de også er kendt som store nøgletræer. Hver node i et B-Tree kan indeholde flere nøgler, hvilket gør det muligt for træet at have en større forgreningsfaktor og dermed en lavere højde. Denne lave højde fører til mindre disk I/O, hvilket resulterer i hurtigere søge- og indsættelsesoperationer. B-Trees er særligt velegnede til lagersystemer, der har langsom, omfangsrig dataadgang, såsom harddiske, flash-hukommelse og cd-rom'er.
B-Trees opretholder balancen ved at sikre, at hver node har et minimum antal nøgler, så træet altid er afbalanceret. Denne balance garanterer, at tidskompleksiteten for operationer såsom indsættelse, sletning og søgning altid er O(log n), uanset træets oprindelige form.
Tidskompleksitet af B-Tree:
| Mr. Nej. | Algoritme | Tidskompleksitet |
|---|---|---|
| 1. | Søg | O(log n) |
| 2. | Indsæt | O(log n) |
| 3. | Slet | O(log n) |
Bemærk: n er det samlede antal elementer i B-træet
c++ konverter int til streng
Egenskaber for B-Tree:
- Alle blade er på samme niveau.
- B-Tree er defineret ved udtrykket minimumsgrad ' t ’. Værdien af ' t ' afhænger af diskblokstørrelsen.
- Hver node undtagen roden skal indeholde mindst t-1 nøgler. Roden må indeholde minimum 1 nøgle.
- Alle noder (inklusive rod) kan højst indeholde ( 2*t – 1 ) nøgler.
- Antal børn af en node er lig med antallet af nøgler i den plus 1 .
- Alle nøgler i en node er sorteret i stigende rækkefølge. Barnet mellem to nøgler k1 og k2 indeholder alle nøgler i området fra k1 og k2 .
- B-Tree vokser og krymper fra roden, hvilket er i modsætning til Binary Search Tree. Binære søgetræer vokser nedad og skrumper også nedad.
- Som andre afbalancerede binære søgetræer er tidskompleksiteten til at søge, indsætte og slette O(log n).
- Indsættelse af en Node i B-Tree sker kun ved Leaf Node.
Følgende er et eksempel på et B-træ med minimum ordre 5
Bemærk: at i praktiske B-Trees er værdien af minimumsordren meget mere end 5.

Vi kan se i ovenstående diagram, at alle bladknuderne er på samme niveau, og alle ikke-blade har intet tomt undertræ og har nøgler en mindre end antallet af deres børn.
Interessante fakta om B-Trees:
- Den mindste højde af B-træet, der kan eksistere med n antal noder og m er det maksimale antal børn af en node kan have, er:
- Den maksimale højde af B-træet, der kan eksistere med n antal noder, og t er det mindste antal børn, som en ikke-rodknude kan have, er:
og
Traversering i B-Tree:
Traversal ligner også Inorder traversal af binært træ. Vi starter fra barnet længst til venstre, udskriver rekursivt barnet længst til venstre og gentager derefter den samme proces for de resterende børn og nøgler. Til sidst skal du rekursivt udskrive barnet længst til højre.
Søgeoperation i B-Tree:
Søgning ligner søgningen i Binary Search Tree. Lad nøglen, der skal søges, er k.
- Start fra roden og gå rekursivt ned.
- For hver besøgt ikke-bladsknude,
- Hvis noden har nøglen, returnerer vi blot noden.
- Ellers går vi tilbage til det passende barn (Barnet, som er lige før den første større nøgle) af noden.
- Hvis vi når en bladknude og ikke finder k i bladknuden, så returner NULL.
At søge i et B-træ svarer til at søge i et binært træ. Algoritmen ligner og går med rekursion. På hvert niveau er søgningen optimeret, som om nøgleværdien ikke er til stede i forælderens område, så er nøglen til stede i en anden gren. Da disse værdier begrænser søgningen, er de også kendt som grænseværdier eller separationsværdier. Hvis vi når en bladknude og ikke finder den ønskede nøgle, vil den vise NULL.
Algoritme til at søge efter et element i et B-træ:-
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->tast[i]) {> >i++;> >}> >if> (i n && k == x->nøgle[i]) {> >return> x;> >}> >if> (x->blad) {> >return> nullptr;> >}> >return> BtreeSearch(x->barn[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1 if i og k == x.key[i]: return x if x.leaf: return Ingen returner BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Eksempler:
fuld form af i d e
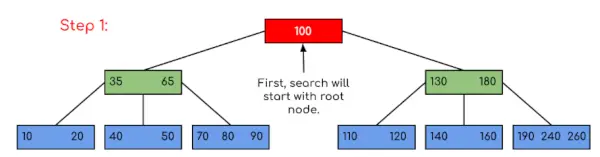
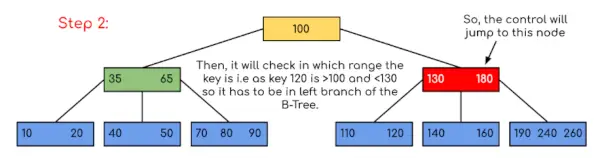
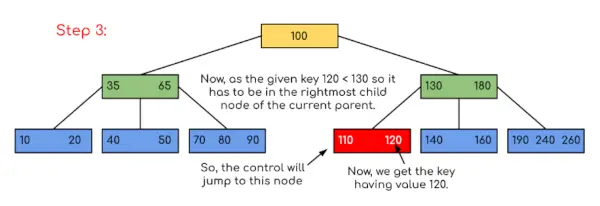
Input: Søg 120 i det givne B-træ.
Løsning:
sæt afgrænser java
I dette eksempel kan vi se, at vores søgning blev reduceret ved blot at begrænse chancerne for, at nøglen med værdien kunne være til stede. På samme måde, hvis vi i ovenstående eksempel skal kigge efter 180, så stopper kontrollen ved trin 2, fordi programmet vil finde, at nøglen 180 er til stede i den aktuelle knude. Og på samme måde, hvis det skal opsøge 90, så som 90 <100, så det vil automatisk gå til venstre undertræ, og derfor vil kontrolflowet gå på samme måde som vist i ovenstående eksempel.
Nedenfor er implementeringen af ovenstående tilgang:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->søg(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->traverse(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->traverse(); } // Funktion til at søge efter nøgle k i undertræ med rod med denne node BTreeNode* BTreeNode::search(int k) { // Find den første nøgle større end eller lig med k int i = 0; while (i taster[i]) i++; // Hvis den fundne nøgle er lig med k, returner denne node, hvis (nøgler[i] == k) returnerer denne; // Hvis nøglen ikke findes her, og dette er en bladknude, hvis (blad == sand) returnerer NULL; // Gå til det relevante underordnede return C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 og k[0] 0]: i -= 1 i += 1 hvis len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) hvis k[0]> x.taster[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Split barnet def split_child(selv, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.taster[t: (2 * t) - 1] y.taster = y.taster[0: t - 1] hvis ikke y.blad: z.barn = y.barn[t: 2 * t] y. child = y.child[0: t - 1] # Udskriv træet def print_tree(selv, x, l=0): print('Niveau ', l, ' ', len(x.keys), end=':') for i i x.keys: print(i, end=' ') print() l += 1 hvis len(x.child)> 0: for i i x.child: self.print_tree(i, l) # Søg tast i træet def search_key(self, k, x=Ingen): hvis x ikke er Ingen: i = 0 mens i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Bemærk: Ovenstående kode indeholder ikke driverprogrammet. Vi vil dække hele programmet i vores næste indlæg B-træ indsættelse .
Der er to konventioner til at definere et B-træ, den ene er at definere ved minimumsgrad, den anden er at definere efter rækkefølge. Vi har fulgt minimumsgradskonventionen og vil følge det samme i kommende indlæg på B-Tree. Variabelnavnene, der bruges i ovenstående program, bevares også de samme
sortering array i java
Anvendelser af B-træer:
- Det bruges i store databaser til at få adgang til data gemt på disken
- Søgning efter data i et datasæt kan opnås på væsentligt kortere tid ved at bruge B-Tree
- Med indekseringsfunktionen kan indeksering på flere niveauer opnås.
- De fleste af serverne bruger også B-tree tilgangen.
- B-Trees bruges i CAD-systemer til at organisere og søge geometriske data.
- B-Trees bruges også på andre områder såsom naturlig sprogbehandling, computernetværk og kryptografi.
Fordele ved B-træer:
- B-Trees har en garanteret tidskompleksitet på O(log n) til grundlæggende operationer som indsættelse, sletning og søgning, hvilket gør dem velegnede til store datasæt og realtidsapplikationer.
- B-træer er selvbalancerende.
- Høj samtidighed og høj kapacitet.
- Effektiv lagerudnyttelse.
Ulemper ved B-træer:
- B-Trees er baseret på disk-baserede datastrukturer og kan have et højt diskforbrug.
- Ikke det bedste for alle tilfælde.
- Langsomt i forhold til andre datastrukturer.
Indsættelse og sletning:
B-træ indsættelse
B-træsletning