Volumen af ​​en trekantet pyramide findes ved hjælp af formlen V = 1/3A.H . En trekantet pyramide, også kendt som et tetraeder, er en type pyramide med en trekantet base og tre trekantede flader, der mødes på et enkelt punkt kaldet apex.

java tuple

I denne artikel vil vi lære om, pyramidedefinition, trekantet pyramidedefinition, trekantet pyramideformel, eksempler og andre i detaljer.

Indholdsfortegnelse

• Hvad er en pyramide?
• Trekantet pyramide definition
• Trekantet pyramideformel
• Overfladeareal af en trekantet pyramide
• Volumen af ​​en trekantet pyramide

Hvad er en pyramide?

EN pyramide er klassificeret i forskellige slags baseret på basens form, såsom en trekantet pyramide, en firkantet pyramide, en femkantet pyramide, en sekskantet pyramide osv. En apex er et mødested for sidefladerne eller sidefladerne af en pyramide . Den vinkelrette afstand fra spidsen af ​​en pyramide til midten af ​​dens base er højden eller højden af ​​en pyramide. Den vinkelrette afstand mellem spidsen og bunden af ​​en skrå højde af en pyramides sideflade.

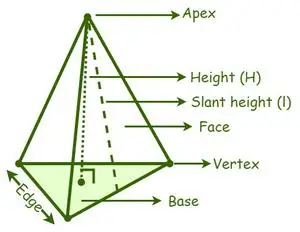
Pyramide

Trekantet pyramide definition

Trekantet pyramide er en pyramide, der har en trekant som sin base. Det er også kendt som et tetraeder og har tre trekantede flader og en trekantet base, hvor den trekantede base kan være skalar, ligebenet eller en ligesidet trekant. En trekantet er yderligere klassificeret i tre typer, dvs. en regulær trekantet pyramide, en uregelmæssig trekantet pyramide og en retvinklet trekantet pyramide.

• Almindelig trekantet pyramide: En trekantet pyramide, hvis fire flader er ligesidede trekanter, kaldes en regulær trekantet pyramide. Da pyramiden består af ligesidede trekanter, er målet for alle dens indre vinkler 60°.

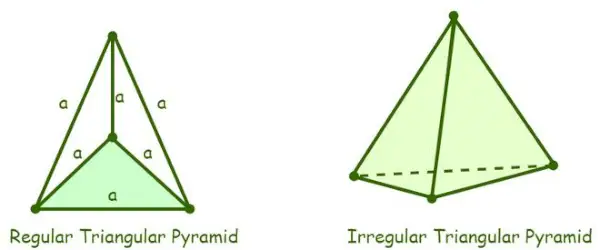
Trekantet pyramide definition

• Uregelmæssig trekantet pyramide: En uregelmæssig trekantet pyramide er en, hvis kanter af basen ikke er ens, dvs. bunden af ​​en uregelmæssig trekantet pyramide er enten en skalaen trekant eller en ligebenet trekant. Alle trekantede pyramider antages at være regulære trekantede pyramider, medmindre en trekantet pyramide specifikt er nævnt som uregelmæssig.

• Højre trekantet pyramide: En retvinklet trekantet pyramide er en, hvis base er en retvinklet trekant, og hvis spids er justeret over midten af ​​basen.

Trekantet pyramideformel

Der er to formler for en trekantet pyramide: overfladearealet af en trekantet pyramide og volumenet af en trekantet pyramide.

• Overfladeareal af en trekantet pyramide
  • Lateral overfladeareal af en trekantet pyramide
  • Samlet overfladeareal af en trekantet pyramide
• Volumen af ​​en trekantet pyramide

Overfladeareal af en trekantet pyramide

Overfladearealet af en pyramide har to typer overfladearealer, nemlig: det laterale overfladeareal og det samlede overfladeareal, hvor overfladearealet af en pyramide er summen af ​​arealerne af sidefladerne eller sidefladerne og grundarealet af en pyramide.

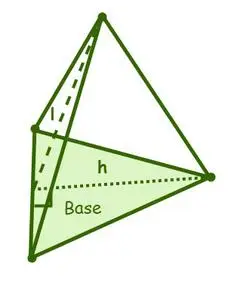
Overfladeareal af en trekantet pyramide

Lateral overfladeareal af en trekantet pyramide

Lateral overfladeareal af en trekantet pyramide beregnes ved hjælp af formlen:

Lateral overfladeareal af en trekantet pyramide (LSA) = ½ × perimeter × skrå højde

Samlet overfladeareal af en trekantet pyramide

Det samlede overfladeareal af en pyramide (TSA) = Lateral overfladeareal af pyramiden + Arealet af basen

Så TSA = ½ × perimeter × skrå højde + ½ × base × højde

Samlet overfladeareal af en trekantet pyramide (TSA) = ½ × P × l + ½ bh

hvor,

• P er perimeter af base
• l er Skråhøjde af Pyramiden
• b er base af trekant ved base
• h er Pyramidens højde

Volumen af ​​en trekantet pyramide

Volumen af ​​en pyramide er det samlede rum indesluttet mellem alle flader af en pyramide. Volumenet af en pyramide er generelt repræsenteret af bogstavet V, og dens formel er lig med en tredjedel af produktet af grundarealet og pyramidens højde.

Formlen for volumen af ​​en pyramide er givet som følger:

Volumen af ​​en trekantet pyramide = 1/3 × grundflade × højde

V = 1/3 × AH kubikenheder

hvor,

• I er Volumen af ​​Pyramiden
• EN er Area of ​​Base of a Pyramide
• H er højden eller højden af ​​en pyramide

Formlen for volumen af ​​en regulær trekantet pyramide er givet som følger

Volumen af ​​regulær trekantet pyramide = a ³ /6√2 kubikenheder

Hvor -en er Kanternes Længde

Atikel relateret til trekantet pyramide:

• Rektangulær pyramide
• Firkantet pyramide
• Femkantet pyramide
• Sekskantet pyramide
• Volumen af ​​en pyramideformel
• Overfladeareal af en pyramideformel

Eksempler på trekantet pyramideformel

Eksempel 1: Bestem rumfanget af en trekantet pyramide, hvis grundareal og højde er 50 cm ² og henholdsvis 12 cm.

Løsning:

Givet data,

• Areal af den trekantede base = 100 cm²
• Pyramidens højde = 12 cm

Vi ved det,

Volumen af ​​en trekantet pyramide (V) = 1/3 × Areal af trekantet base × Højde

H = 1/3 × 50 × 12 = 200 cm³

Derfor er volumenet af den givne trekantede pyramide 200 cm³.

Eksempel 2: Find det samlede overfladeareal af en almindelig trekantet pyramide, når længden af ​​hver kant er 8 tommer.

Løsning:

Givet data,

• Længden af ​​hver kant af en regulær trekantet pyramide (a) = 8 tommer

Vi ved det,

Samlet overfladeareal af en regulær trekantet pyramide = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110.851 sq. in

Derfor er det samlede overfladeareal af en regulær trekantet pyramide 110.851 sq. in.

Eksempel 3: Bestem rumfanget af en regulær trekantet pyramide, når kantens længde er 10 cm.

Løsning:

Givet data,

• Længde af hver kant af en regulær trekantet pyramide (a) = 10 cm

Vi ved det,

Volumen af ​​en regulær trekantet pyramide = a³/6√2

omvendt streng java

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 cm³

Derfor er volumenet af en regulær trekantet pyramide 117,85 cu. cm.

Eksempel 4: Find skråhøjden af ​​den trekantede pyramide, hvis dens laterale overfladeareal er 600 sq. in. og omkredsen af ​​basen er 60 inches.

Løsning:

Givet data,

• Sidefladeareal = 600 sq. in
• Basens omkreds = 60 tommer

Vi ved det,

Sidefladeareal = ½ × perimeter × skrå højde

600 = ½ × 60 × l

l = 600/30 = 20 tommer

Derfor er skråhøjden af ​​den givne pyramide 20 tommer.

Eksempel 5: Bestem det samlede overfladeareal af en trekantet pyramide, hvis grundareal er 28 cm2, trekantens omkreds er 18 cm, og pyramidens skråhøjde er 20 cm.

Løsning:

Givet data,

• Areal af trekantet base = 28 cm²
• Skråhøjde (l) = 20 cm
• Omkreds (P) = 18 cm

Vi ved det,

Samlet overfladeareal (TSA) af en trekantet pyramide = ½ × perimeter × skrå højde + basisareal

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 cm2

Derfor er det samlede overfladeareal af den givne pyramide 208 sq. cm.

Øv problemer på trekantet pyramideformel

Q1. Givet en trekantet pyramide med et grundareal på 15 kvadratenheder og en højde på 10 enheder, hvad er volumen af ​​pyramiden?

Q2. Givet en regulær trekantet pyramide, hvor hver kant af den ligesidede trekantede base måler 6 enheder, hvad er pyramidens samlede overfladeareal?

Q3. Givet en regulær trekantet pyramide, hvor hver kant af den ligesidede trekantede base måler 4 enheder og en højde på 5 enheder, hvad er volumen og det samlede overfladeareal af pyramiden?

Q4. Hvis sidelængderne af bunden af ​​en trekantet pyramide er 3 enheder, 4 enheder og 5 enheder, og pyramidens højde er 12 enheder, hvad er pyramidens rumfang?

Q5. For en trekantet pyramide med en base i form af en retvinklet trekant med ben på 3 enheder og 4 enheder og hypotenus på 5 enheder, hvad er det samlede overfladeareal, hvis højden af ​​pyramiden fra bunden til spidsen er 10 enheder ?

Ofte stillede spørgsmål om trekantet pyramideformel

Hvad er definitionen af ​​en trekantet pyramide?

En trekantet pyramide er en geometrisk form, der har en trekantet base og tre trekantede flader, der har et fælles toppunkt.

Hvor mange ansigter og hjørner har en trekantet pyramide?

Trekantet pyramide har fire flader og fire hjørner. Et toppunkt er fælles for alle tre flader af pyramiden.

Hvad er den grundlæggende formel for en pyramide?

Grundlæggende formler for en pyramide er:

• LSA = ½ × Perimeter × Skråhøjde
• TSA = ½ × P × l + ½ bh
• V = 1/3 × AH

Hvad er typer af trekantede pyramider?

Der er tre typer trekantede pyramider, som er

• Almindelig trekantet pyramide
• Uregelmæssig trekantet pyramide
• Retvinklet trekantet pyramide

Hvad er formel for trekanter?

Formlen for trekantens areal er:

• (Areal)A = 1/2 × b × h