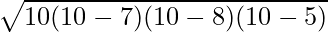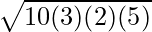Akut vinklet trekant er en trekant, hvor alle vinklerne i trekanterne er spidse vinkler. En trekant kan kun have én vinkel som enten ret vinkel eller stump vinkel på grund af trekantens vinkelsum egenskab. Og derfor kaldes trekanten med alle tre vinkler som spidse vinkler, dvs. vinkler med en værdi mindre end 90 grader, en spidsvinklet trekant.
Baseret på typerne af indvendige vinkler i trekanten kan en trekant klassificeres i tre kategorier: Akutvinklede trekanter, stumpvinklede trekanter og retvinklede trekanter. Lad os nu lære mere om spidsvinklede trekanter, deres typer, egenskaber og andre i detaljer i denne artikel.
Hvad er en akutvinklet trekant?
An spidsvinklet trekant er defineret som en trekant, hvis alle tre indre vinkler er spidse, dvs. deres værdi er mellem 0° og 90°. Baseret på typen af trekant kan sidelængderne af en spidsvinklet trekant være lige store eller ulige. En spidsvinklet trekant følger også trekantens vinkelsum-egenskab.
Figuren nedenfor er en spidsvinklet trekant, hvis indre vinkler er 45°, 35° og 80°. Da de tre indre vinkler er mindre end 90°, er den givne trekant en spidsvinklet trekant.
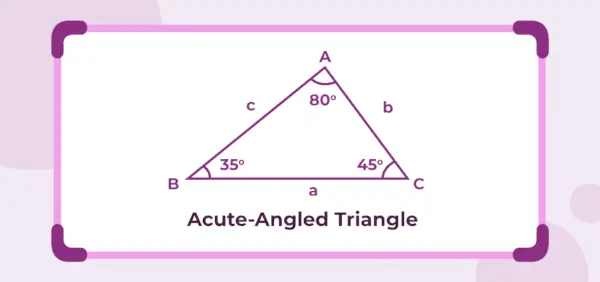
Akutvinklet trekant Definition
Akutvinklede trekanter defineres, som navnet antyder, som trekanter, hvor alle tre vinkler i trekanten er spidse vinkler. Siden i spidsvinklede trekanter kan være ens eller ulige og ud fra det er de yderligere opdelt i tre dele, der diskuteres i artiklen nedenfor,
Typer af akutvinklede trekanter
Akutvinklede trekanter er klassificeret i tre typer afhængigt af sidelængderne af trekanter,
- Ligesidet akut trekant
- Ligebenet Akut Trekant
- Scalene Akut Trekant
Lad os nu lære mere om dem i detaljer.
Ligesidet akut trekant
En ligesidet spids trekant også kaldet en ligesidet trekant er en trekant, hvor alle vinklerne er spidse vinkler, og alle vinklerne er lige, også siden af de ligesidede spidse trekanter er også lige store. Hver vinkel i en ligesidet spids trekant måler altid 60°.
Ligebenet Akut Trekant
En ligebenet spids trekant er en trekant, hvor alle vinklerne er spidse vinkler, og alle to vinkler i trekanten og den side, der svarer til disse vinkler, er lige store. Det vil sige, at vi i den ligebenede spidse trekant har to sider og deres tilsvarende vinkler ens.
Scalene Akut Trekant
En skalen spids trekant er en trekant, hvor alle vinklerne er spidse vinkler, og ingen to vinkler og ingen to sider er ens. Det vil sige, at vi i den spidse trekant ikke har nogen sider og ingen vinkler ens.
Egenskaber ved Akutvinklet Trekant
Følgende er nogle vigtige egenskaber ved en spidsvinklet trekant,
- Indvendige vinkler af den spidsvinklede trekant er spidse vinkler, dvs. vinklerne er større end 0° men mindre end 90°.
- Indvendige vinkler i de spidsvinklede trekanter følger vinkelsumegenskaben, dvs. summen af vinklerne i den spidsvinklede trekants er 180°.
- En ligesidet trekant er altid en spidsvinklet trekant, da hver indre vinkel i en ligesidet trekant måler 60°.
- En trekant kan ikke samtidig være en retvinklet trekant og en spidsvinklet trekant.
- En trekant kan ikke samtidig være en spidsvinklet trekant og en stumpvinklet trekant.
- I den spidse vinkeltrekant er siden modsat den mindste vinkel den mindste, og dens modsætning er også sand.
- På samme måde er siden modsat den største vinkel den største, og dens omvendte er også sandt.
Akutvinklede trekantformler
Arealet og omkredsen er de to grundlæggende formler for en spidsvinklet trekant, som diskuteres nedenfor.
Omkreds af akut-vinklet trekant
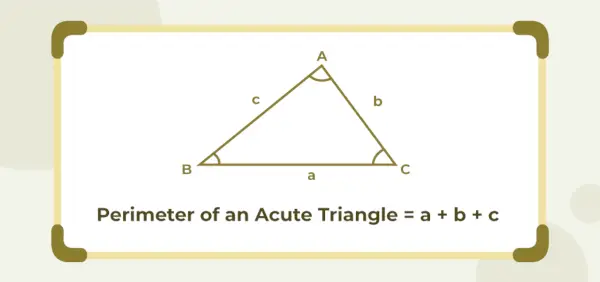
Omkredsen af en spidsvinklet trekant er lig med summen af dens tre sidelængder. Hvis a, b og c er sidelængderne af en spidsvinklet trekant, så er dens omkreds givet som (a + b + c) enheder.
Omkreds af akutvinklet trekant = (a + b + c) enheder
Hvor -en , b , og c er trekantens sidelængder.
Læs mere, Omkreds af en trekant
Området med spidsvinklet trekant
Arealet af en trekant er defineret som det samlede rum omgivet af de tre sider af en trekant i et todimensionalt plan.
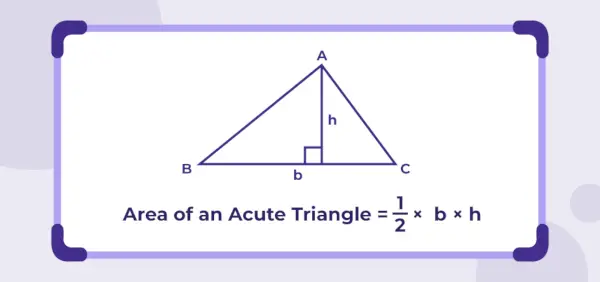
Areal af spidsvinklet trekant = ½ × b × h
Hvor,
b er grundlængden, ogh er højden af trekanten.
Læs mere, Areal af en trekant
Acute Triangle Area af Heron's Formula
Hvis de tre sidelængder af en spidsvinklet trekant er givet, kan dens areal beregnes ved hjælp af Herons formel.
streng i array i c
Areal af spidsvinklet trekant =
Hvor,
s er semi-perimeteren og s = (a + b + c)/2 , dig , b , og c er trekantens sidelængder.
Læs mere, Herons formel
Vigtige terminologier i trekanten
De forskellige terminologier relateret til den spidsvinklede trekant er,
Omkring centrum
Centret af cirklen, der passerer trekantens tre spidser, kaldes trekantens circumcenter. Det beregnes ved at tage skæringspunktet for den vinkelrette halveringslinje. For en spidsvinklet trekant ligger circumcenter altid inde i trekanten.
Incenter
Centret af cirklen, der rører trekantens tre sider, kaldes trekantens midte. Det beregnes ved at tage skæringspunktet for vinkelhalveringslinjen. For en spidsvinklet trekant ligger incentret altid inde i trekanten.
Centroid
Skæringspunktet mellem en trekants medianer kaldes trekantens tyngdepunkt. For en spidsvinklet trekant ligger trekantens tyngdepunkt altid inde i trekanten.
Ortocenter
Skæringspunktet for trekantens højde kaldes trekantens ortocenter. For en spidsvinklet trekant ligger trekantens ortocenter altid inde i trekanten.
Løste eksempler på akut vinklet trekant
Eksempel 1: Hvilken af følgende vinkler kan danne en spidsvinklet trekant?
- a) 65°, 75°, 50° b) 95°, 40°, 45° c) 70°, 40°, 70° d) 90°, 45°, 45°
Løsning:
Vi ved, at alle vinklerne i den spidsvinklede trekant er spidse vinkler, hvilket betyder, at deres mål er mindre end 90 grader.
De følger også vinkelsumegenskaben for en trekant, dvs. alle deres vinkler summerer op til 180 grader.
en) 65°, 75°, 50°
Her er alle vinklerne spidse vinkler, men det følger ikke vinkelsumegenskaben, hvorfor trekanten ikke er mulig.
65°+ 75°+ 50° = 190° (Trekant ikke mulig)
b) 95°, 40°, 45°
Her er trekanten mulig, da den følger trekantens vinkelsumegenskab, dvs.
95°+ 40°+ 45° = 180
Men mens vi observerede trekantens vinkler fandt vi en stump vinkel på 95°. Derfor er trekanten ikke en spidsvinklet trekant.
c) 70°, 40°, 70°
Her er trekanten mulig, da den følger trekantens vinkelsumegenskab, dvs.
70°+ 40°+ 70° = 180
Og mens vi observerede vinklerne i trekanten fandt vi ud af, at alle vinklerne er spidse vinkler. Derfor er trekanten en spidsvinklet trekant.
d) 90°, 45°, 45°
Her er trekanten mulig, da den følger trekantens vinkelsumegenskab, dvs.
90°+ 45°+ 45° = 180
Men mens vi observerede trekantens vinkler fandt vi en ret vinkel på 90°. Derfor er trekanten ikke en spidsvinklet trekant.
Eksempel 2: Find omkredsen af en spids trekant XYZ, hvis sider er XY = 8 enheder, YZ = 5 enheder og XZ = 9 enheder.
Løsning:
givet,
Sider af akut-vinklet trekant,
- XY(x) = 8 enheder
- YZ(y) = 5 enheder
- XZ(z) = 9 enheder
Vi ved det,
Omkreds af akutvinklet trekant (P) = x + y + z
⇒ P = (8 + 5 + 9) enheder
⇒ P = 22 enheder
Derfor er omkredsen af den spidsvinklede trekant 22 enheder.
Eksempel 3: Find arealet af en spids trekant, hvis højde er 12 enheder og grundfladen er 15 enheder.
Løsning:
romerske tal 1 til 100
givet,
- Trekantens højde (h) = 12 enheder
- Længde af trekantens base (b) = 15 enheder
Vi ved det,
Areal af trekanten (A) = ½ × b × h
⇒ A = ½ × 12 × 15
⇒ A = ½ × 180
⇒ A = 90 kvadratenheder.
Derfor er arealet af den givne spidse trekant 90 kvadratenheder.
Eksempel 4: Find arealet af en spids trekant, hvis sider er AB = 5 cm, BC = 7 cm og AC = 8 cm.
Løsning:
givet,
Sider af akut-vinklet trekant,
- AB = c = 5 enheder
- BC = a = 7 enheder
- AC = b = 8 enheder
Vi ved det,
Areal af trekanten =
⇒ A =
⇒ A =
⇒ A = √(300) sq. cm
⇒ A = 10√3 cm2
Derfor er arealet af den givne spidse trekant 10√3 sq. cm.
Ofte stillede spørgsmål om Akut vinklet trekant
Q1: Hvad er akutte vinkler?
Svar:
Vinklen, der går fra 0° til 90° kaldes de spidse vinkler. Det vil sige, at den mindste værdi af den spidse vinkel er større end 0°, og den maksimale værdi af den spidse vinkel er større end 90°.
Q2: Hvad er en akutvinklet trekant?
Svar:
En spidsvinklet trekant er en trekant, hvis alle tre indre vinkler er spidse vinkler, dvs. værdien af vinklen er mellem 0° og 90°.
Spørgsmål 3: Er en ligesidet trekant altid en spidsvinklet trekant?
Svar:
Ja, en ligesidet trekant er altid en spidsvinklet trekant. En spidsvinklet trekanter er de vinkler, der har alle vinkler har spidse vinkler, og i euqilateral trekant er alle vinklerne 60°, dvs. spidse vinkler. Derfor er en ligesidet trekant altid en spidsvinklet trekant.
Q4: Hvad er de forskellige typer af akut-vinklede trekanter?
Svar:
Akutvinklede trekanter er klassificeret i tre typer, som er,
- Scalene Akut Trekant
- Ligebenet Akut Trekant
- Ligesidet akut trekant
Spørgsmål 5: Hvordan ved man, om en trekant er en spidsvinklet trekant?
Svar:
En trekant, hvis indre vinkler er mindre end 90°, dvs. alle de indre vinkler er spidse vinkler, så kaldes trekanten den spidsvinklede trekant. Vi kan kontrollere, om trekanten er en spidsvinklet trekant, ved blot at observere trekantens vinkler.