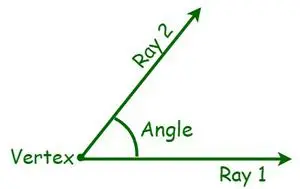
I geometri er en vinkel en væsentlig måling af en geometrisk form. En vinkel er defineret som graden af rotation omkring skæringspunktet mellem to linjer eller planer, der er nødvendige for at bringe den ene i overensstemmelse med den anden. Der findes forskellige slags vinkler, baseret på måling af en vinkel. Det måles i grader eller radianer. En vinkel er en form dannet af to linjer eller stråler, der divergerer fra et fælles punkt kaldet et vertex. Når to stråler skæres, dvs. når halvlinjer projiceres med et fælles endepunkt, dannes en vinkel. Nu kaldes de fælles endepunkter hjørner, mens strålerne er kendt som armene.
Typer af vinkler

- Spids vinkel: En spids vinkel er en vinkel, der er større end 0 grader og mindre end 90 grader, dvs. den varierer fra 0° til 90° (begge eksklusive).
- Ret vinkel: En ret vinkel kaldes den vinkel, der måler præcis 90 grader.
- Stump vinkel: En stump vinkel er en vinkel, der er større end 90 grader og mindre end 180 grader, dvs. den varierer fra 90° til 180° (begge eksklusive).
- Lige vinkel: En lige vinkel omtales som en vinkel, der måler præcis 180 grader.
- Refleks vinkel: En refleksvinkel er en vinkel, der er større end 180 grader og mindre end 360 grader, dvs. den spænder fra 180° til 360° (begge eksklusive).
- En komplet vinkel eller fuld rotation: En komplet vinkel omtales som den vinkel, der måler nøjagtigt 360 grader.
Der er også andre typer vinkler, såsom komplementære vinkler, supplerende vinkler og tilstødende og ikke-tilstødende vinkler.
- Komplementære vinkler: To vinkler siges at være komplementære, hvis deres sum er en ret vinkel, dvs. 90°.
- Supplerende vinkler: To vinkler siges at være supplerende, hvis deres sum er lig med 180°.
- Tilstødende vinkler: To vinkler siges at være tilstødende, hvis de deler et fælles toppunkt og en fælles arm.
- Ikke-tilstødende vinkler: To vinkler siges at være ikke-tilstødende, hvis de ikke deler et fælles toppunkt og en fælles arm.
Formlen til at finde vinkler
Der findes forskellige typer formler til at finde en vinkel; nogle af dem er den centrale vinkelformel, dobbeltvinkelformlen, halvvinkelformlen, den sammensatte vinkelformel, den indre vinkelformel osv.
- Vi bruger den centrale vinkelformel til at bestemme vinklen på et segment lavet i en cirkel.
- Vi bruger summen af formlen for indre vinkler til at bestemme den manglende vinkel i en polygon.
- Vi bruger de trigonometriske forhold til at finde den manglende vinkel i en retvinklet trekant.
- Vi bruger sinusloven eller cosinusloven til at finde den manglende vinkel i en ikke-retvinklet trekant.
Formlens navn | Formel | Hvordan finder man en ukendt vinkel? |
|---|---|---|
| Centralvinkelformel | θ =(s × 360°)/2prHer er s buelængden og r er cirklens radius | Erstat værdierne af buelængde og radius af cirklen for at bestemme vinklen på et segment lavet i en cirkel. |
| Summen af indvendige vinkler Formel | 180°(n-2)Her er n antallet af sider af en polygon | For at bestemme den ukendte indre vinkel af en polygon skal du først beregne summen af alle indvendige vinkler ved hjælp af denne formel og derefter trække summen af alle kendte vinkler fra resultatet. svæver i css |
| Trigonometriske forhold | sin θ = modsatte side/hypotenusecos θ = tilstødende side/hypotenusetan θ = modsat side/tilstødende side | Afhængigt af de tilgængelige to sider af en retvinklet trekant skal du vælge et af disse trigonometriske forhold for at finde den ukendte vinkel. |
| Sines lov | a/sin A = b/sin B = c/sin CHer er A, B og C de indre vinkler af en trekant, og a, b og c er deres respektive modsatte sider. | Når vi kender to sider og en ikke-inkluderet vinkel (eller) to vinkler og en ikke-inkluderet side, så kan loven om sinus bruges til at bestemme de ukendte vinkler i en trekant. |
| Cosinusloven | -en2= b2+ c2– 2bc cos Ab2= c2+ a2– 2ca cos Bc2= a2+ b2– 2ab cos CHer er A, B og C de indre vinkler af en trekant, og a, b og c er deres respektive modsatte sider. | Når vi kender tre sider (eller) to sider og en inkluderet vinkel, så kan cosinusloven bruges til at bestemme de ukendte vinkler i en trekant. |
Eksempel på spørgsmål
Spørgsmål 1: Find vinklen ved toppunktet B i den givne trekant ved hjælp af en af de trigonometriske formler til at finde vinkler.

Løsning:
givet,
BC = 3 enheder = Tilstødende side af θ.
AC = 4 enheder = Modsat side af θ.
I dette tilfælde kender vi både de modsatte og tilstødende sider af θ. Derfor kan vi bruge tangentformlen til at finde θ.
⇒ tan θ = modsat side/tilstødende side
⇒ tan θ = 4/3
⇒ θ = tan-1(4/3) ⇒ θ = 53,1°
Derfor er vinklen ved toppunktet B 53,1°.
Spørgsmål 2: Find vinklerne ved hjørnerne X og Y, hvis ∠Z = 35° og x = 3 tommer, y = 8 tommer og z = 3,5 tommer.

Løsning:
givet,
vandmærke i word∠Z = 35° og x = 6 tommer, y = 3 tommer og z = 3,5 tommer
Da vi kender alle tre sider og en vinkel, kan vi bruge sinusregelformlen.
Fra sinusregelformlen har vi
x/sin X = y/sin Y = z/sin Z
Nu,
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/uden Y = 3,5/0,574 {Siden, sin 35° = 0,574}
alfabet af tal⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = synd−1(0,492) = 29,47°
Vi ved, at summen af tre vinkler i en trekant er 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Derfor er ∠X = 115,53° og ∠Y = 29,47°.
Spørgsmål 3: Beregn den femte indre vinkel af en femkant, hvis fire af dens indre vinkler er 110°, 85°, 136° og 105°.
Løsning:
Antallet af sider af en femkant (n) = 5.
Nu er summen af alle 5 indre vinkler af en femkant = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Summen af de givne 4 indvendige vinkler = 110°+ 85°+ 136°+ og 105°= 436°.
Så den femte indre vinkel = 540° – 436° = 104°
Således er den femte indre vinkel af en femkant 104°.
Spørgsmål 4: Bestem værdien af y og også målet for vinkler i den givne figur.

Løsning:
Fra den givne figur kan vi observere, at (4y – 6)° og (3y + 5)° er komplementære vinkler, dvs. summen af (4y – 6)° og (3y + 5)° er 90 °.
⇒ (4y – 6)° + (3y + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Nu, (4y – 6)° = (4 ×13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Spørgsmål 5: Find vinklen ved toppunktet Q i den givne trekant ved hjælp af en af formlerne til at finde vinkler.

Løsning:
Givet, p = QR = 6 cm, q = PR = 9 cm, og r = PQ = 7 cm.
Da vi kender alle tre sider og en vinkel, kan vi bruge cosinusreglen til at finde vinkelspidsen Q.
markdown fodnoter⇒ q2= s2+ r2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6)(7) med Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Derfor er vinklen ved toppunktet Q, ∠Q = 92,72°.
Spørgsmål 6: Beregn vinklen på et segment lavet i en cirkel, hvis buelængden er 12π og radius er 9 cm.
Løsning:
givet,
Buelængden = 12π
Radius (r) = 9 cm
Nu er vinkelformlen:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 × 360°/10
hvad er desktop ini⇒ θ = 240°
Derfor er vinklen 240°.
