I denne artikel vil vi diskutere trægennemgangen i datastrukturen. Udtrykket 'trægennemgang' betyder at krydse eller besøge hver knude i et træ. Der er en enkelt måde at krydse den lineære datastruktur, såsom linket liste, kø og stak. Mens der er flere måder at krydse et træ på, der er angivet som følger -
- Forudbestil gennemløb
- Gennemgang af uorden
- Postordregennemgang
Så i denne artikel vil vi diskutere de ovennævnte teknikker til at krydse et træ. Lad os nu begynde at diskutere måderne at krydse træer på.
Forudbestil gennemløb
Denne teknik følger 'root left right'-politikken. Det betyder, at den første rodknude besøges, efter at det venstre undertræ krydses rekursivt, og til sidst krydses det højre undertræ rekursivt. Da rodknuden krydses før (eller før) det venstre og højre undertræ, kaldes det preorder traversal.
Så i en forudbestillingsgennemgang besøges hver node før begge dens undertræer.
Anvendelser af forudbestillingsgennemgang inkluderer -
- Det bruges til at lave en kopi af træet.
- Det kan også bruges til at få præfiksudtrykket for et udtrykstræ.
Algoritme
Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively.
Eksempel
Lad os nu se eksemplet med preorder-traversal-teknikken.
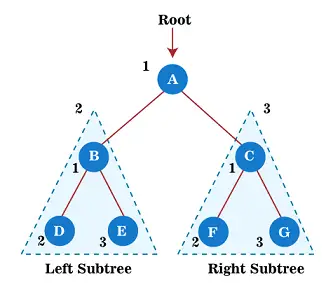
Begynd nu at anvende preorder-gennemgangen på ovenstående træ. Først krydser vi rodknuden EN; derefter flyttes til venstre undertræ B , som også vil blive gennemgået i forudbestilling.
Så for venstre undertræ B, først rodknuden B er traverseret sig selv; derefter dets venstre undertræ D er krydset. Siden node D har ingen børn, flyt til højre undertræ OG . Da knudepunkt E heller ikke har nogen børn, er gennemgangen af venstre undertræ af rodknude A fuldført.
hvordan man bryder ud af en while loop java
Bevæg dig nu mod højre undertræ af rodknude A, der er C. Så for højre undertræ C, først rodknudepunktet C har krydset sig selv; derefter dets venstre undertræ F er krydset. Siden node F ikke har nogen børn, flyt til højre undertræ G . Da node G heller ikke har nogen børn, er gennemgangen af det højre undertræ af rodknude A fuldført.
Derfor krydses alle træets noder. Så outputtet af forudbestillingsgennemgangen af ovenstående træ er -
A → B → D → E → C → F → G
For at vide mere om forudbestillingsgennemgangen i datastrukturen kan du følge linket Forudbestil gennemløb .
Postordregennemgang
Denne teknik følger 'venstre-højre rod'-politikken. Det betyder, at det første venstre undertræ af rodknuden krydses, derefter krydser det højre undertræ rekursivt, og til sidst krydses rodknuden. Da rodknuden krydses efter (eller poster) det venstre og højre undertræ, kaldes det postorder traversal.
Så i en postorder-gennemgang besøges hver node efter begge dens undertræer.
Anvendelserne af postordre-gennemgang omfatter -
array vs arraylist
- Det bruges til at slette træet.
- Det kan også bruges til at få postfix-udtrykket af et udtrykstræ.
Algoritme
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node.
Eksempel
Lad os nu se eksemplet med postorder-traversal-teknikken.

Begynd nu at anvende postorder-gennemgangen på ovenstående træ. Først krydser vi det venstre undertræ B, der vil blive krydset i postordre. Derefter vil vi krydse det rigtige undertræ C i postordre. Og endelig, rodknuden på ovenstående træ, dvs. EN , er krydset.
Så for venstre undertræ B, først dets venstre undertræ D er krydset. Siden node D ikke har nogen børn, skal du krydse det højre undertræ OG . Da node E heller ikke har nogen børn, skal du flytte til rodknuden B. Efter at have krydset knudepunkt B, gennemkørslen af det venstre undertræ af rodknude A er fuldført.
Bevæg dig nu mod det højre undertræ af rodknude A, der er C. Så for højre undertræ C, først dets venstre undertræ F er krydset. Siden node F ikke har nogen børn, skal du krydse det højre undertræ G . Da node G heller ikke har nogen børn, derfor endelig rodknuden på det højre undertræ, dvs. C, er krydset. Gennemgangen af det højre undertræ af rodknude A er fuldført.
Til sidst skal du krydse rodknuden på et givet træ, dvs. EN . Efter at have krydset rodknuden, er postorder-gennemgangen af det givne træ fuldført.
Derfor krydses alle træets noder. Så outputtet af postorder-gennemgangen af ovenstående træ er -
D → E → B → F → G → C → A
For at vide mere om postordre-gennemgangen i datastrukturen kan du følge linket Postordregennemgang .
Gennemgang af uorden
Denne teknik følger politikken 'venstre rod højre'. Det betyder, at det første venstre undertræ besøges, efter at rodknudepunktet er krydset, og til sidst krydses det højre undertræ. Når rodknuden krydses mellem venstre og højre undertræ, kaldes den inorder-gennemgang.
muserul virker ikke
Så i den uordnede gennemgang besøges hver knude mellem dens undertræer.
Anvendelserne af Inorder traversal inkluderer -
- Det bruges til at få BST noderne i stigende rækkefølge.
- Det kan også bruges til at få præfiksudtrykket for et udtrykstræ.
Algoritme
Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively.
Eksempel
Lad os nu se eksemplet med Inorder-traversalteknikken.

Begynd nu at anvende den uordnede traversering på ovenstående træ. Først krydser vi det venstre undertræ B som vil blive krydset i uorden. Derefter vil vi krydse rodnoden EN . Og endelig det rigtige undertræ C krydses i uorden.
Altså for venstre undertræ B , for det første dets venstre undertræ D er krydset. Siden node D har ingen børn, så efter at have krydset det, knude B vil blive krydset, og til sidst højre undertræ af node B, dvs OG , er krydset. Node E har heller ingen børn; derfor er gennemgangen af det venstre undertræ af rodknude A fuldført.
Derefter skal du krydse rodknuden på et givet træ, dvs. EN .
Bevæg dig endelig mod det højre undertræ af rodknude A, der er C. Så for højre undertræ C; først dets venstre undertræ F er krydset. Siden node F har ingen børn, node C vil blive krydset, og til sidst, et højre undertræ af node C, dvs. G , er krydset. Node G har heller ingen børn; derfor er gennemgangen af det højre undertræ af rodknude A fuldført.
hvad er regex java
Efterhånden som alle træets knudepunkter krydses, fuldføres den uordnede krydsning af det givne træ. Outputtet af den uordnede traversering af ovenstående træ er -
D → B → E → A → F → C → G
For at vide mere om inordergennemgangen i datastrukturen, kan du følge linket Inorder Traversal .
Kompleksiteten af trægennemløbsteknikker
Tidskompleksiteten af trægennemløbsteknikker diskuteret ovenfor er På) , hvor 'n' er størrelsen af et binært træ.
Hvorimod pladskompleksiteten af trægennemløbsteknikker diskuteret ovenfor er O(1) hvis vi ikke overvejer stakstørrelsen for funktionskald. Ellers er pladskompleksiteten af disse teknikker O(h) , hvor 'h' er træets højde.
Implementering af trægennemgang
Lad os nu se implementeringen af de ovenfor diskuterede teknikker ved hjælp af forskellige programmeringssprog.
Program: Skriv et program til at implementere trægennemløbsteknikker i C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } Produktion

Program: Skriv et program til at implementere trægennemløbsteknikker i C#.
rohit shetty skuespiller
using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } Produktion

Program: Skriv et program til at implementere trægennemløbsteknikker i C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root->right); cout<<' '<element<left="createNode(28);" root->right = createNode(48); root->left->left = createNode(23); root->left->right = createNode(33); root->left->left->left = createNode(13); root->left->left->right = createNode(26); root->right->left = createNode(43); root->right->right = createNode(58); root->right->right->left = createNode(53); root->right->right->right = createNode(68); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println('
'); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println('
'); System.out.println('The Postorder traversal of given binary tree is - '); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that's all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'> Produktion
Efter udførelse af ovenstående kode vil outputtet være -

Konklusion
I denne artikel har vi diskuteret de forskellige typer trætraversalteknikker: preorder traversal, inorder traversal og postorder traversal. Vi har set disse teknikker sammen med algoritme, eksempel, kompleksitet og implementering i C, C++, C# og java.
Så det handler om artiklen. Håber det vil være nyttigt og informativt for dig.
