I denne artikel vil vi diskutere den uordensgennemgang i datastrukturen.
forskel på ræv og ulv
Hvis vi ønsker at krydse knudepunkterne i stigende rækkefølge, så bruger vi in-order-gennemgangen. Følgende er de nødvendige trin for gennemkørslen af den inordnede rækkefølge:
- Besøg alle noderne i venstre undertræ
- Besøg rodnoden
- Besøg alle noderne i det højre undertræ
Lineære datastrukturer såsom stak, array, kø osv. har kun én måde at krydse dataene på. Men i hierarkiske datastrukturer som f.eks træ, der er flere måder at krydse dataene på. Her vil vi diskutere en anden måde at krydse trædatastrukturen på, dvs. krydsning af uorden.
Der er to tilgange, der bruges til at krydse den uorden:
- Inorder traversal ved hjælp af rekursion
- Inorder traversal ved hjælp af en iterativ metode
En uordens-traversalteknik følger Venstre rod Højre politik. Her betyder Venstre rod Højre, at det venstre undertræ af rodknuden krydses først, derefter rodnoden, og derefter krydses det højre undertræ af rodknuden. Her antyder selve ordensnavnet, at rodknuden kommer ind mellem venstre og højre undertræ.
Vi vil diskutere den inordnede traversal ved hjælp af både rekursive og iterative teknikker. Lad os først starte med in-order traversal ved hjælp af rekursion.
Inordner traversal ved hjælp af rekursion
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Eksempel på gennemkørsel af uorden
Lad os nu se et eksempel på krydsning af uorden. Det vil være nemmere at forstå proceduren for gennemkørsel af uorden ved hjælp af et eksempel.
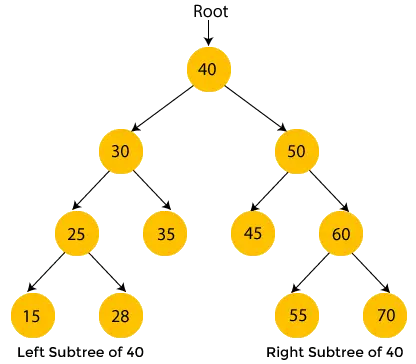
Noderne med gul farve er ikke besøgt endnu. Nu vil vi krydse knudepunkterne i ovennævnte træ ved at bruge inorder-gennemgang.
- Her er 40 rodknuden. Vi flytter til venstre undertræ på 40, altså 30, og det har også undertræ 25, så vi flytter igen til venstre undertræ på 25, der er 15. Her har 15 ikke noget undertræ, så print 15 og bevæg dig mod dens overordnede node, 25.
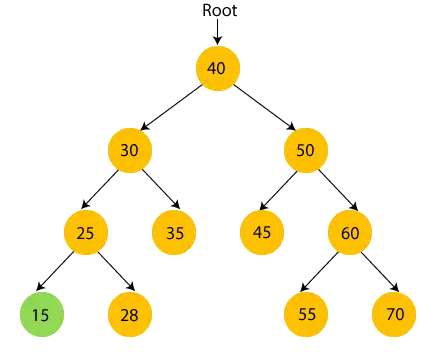
- Nu, print 25 og flyt til højre undertræ af 25.
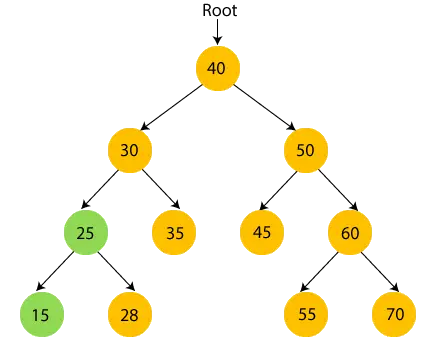
- Nu, print 28 og flyt til rodknuden på 25, dvs. 30.
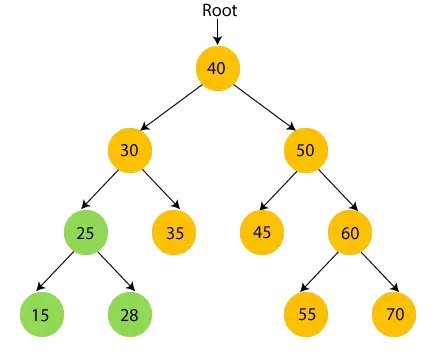
- Så venstre undertræ på 30 er besøgt. Nu, print 30 og flytte til det rigtige barn på 30.
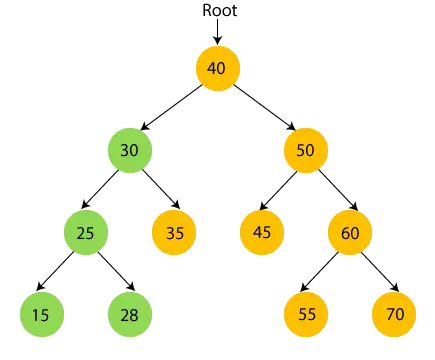
- Nu, print 35 og flyt til rodnoden på 30.
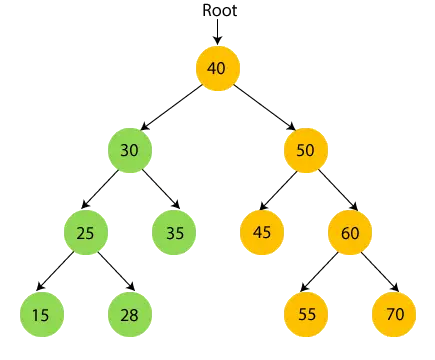
- Nu, udskriv root node 40 og flyt til højre undertræ.
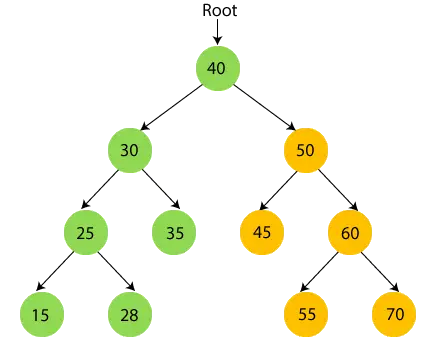
- Gå nu rekursivt gennem det højre undertræ af 40, hvilket er 50.
50 har undertræ, så kryds først det venstre undertræ på 50, dvs. 45. 45 har ingen børn, så print 45 og flyt til dens rodknude.
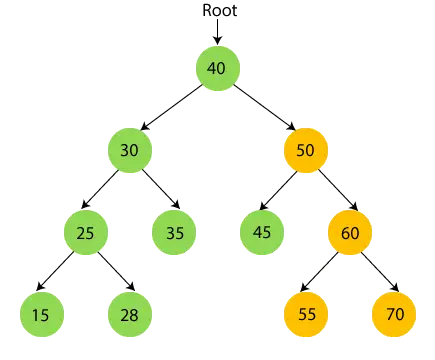
- Nu print 50 og flyt til højre undertræ af 50, hvilket er 60.
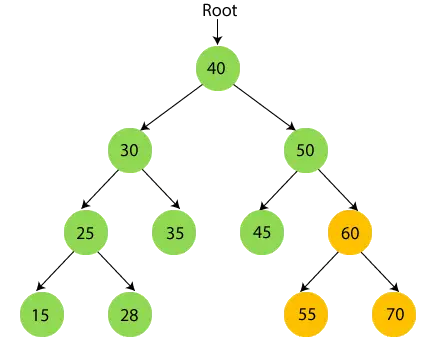
- Gå nu rekursivt gennem det højre undertræ på 50, dvs. 60. 60 har et undertræ, så kryds først det venstre undertræ på 60, som er 55. 55 har ingen børn, så tryk 55 og flyt til dens rodknude.
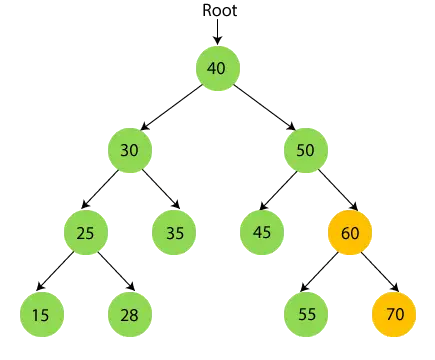
- Nu tryk 60 og flyt til højre undertræ af 60, hvilket er 70.
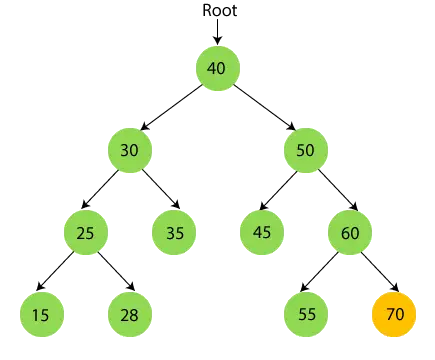
- Nu tryk 70.
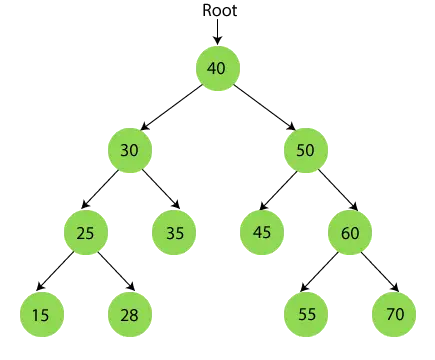
Efter afslutningen af inordergennemgang er det endelige output -
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Kompleksiteten af Inorder-gennemgang
Tidskompleksiteten af Inorder traversal er På), hvor 'n' er størrelsen af binært træ.
Hvorimod rumkompleksiteten ved gennemkørsel af uorden er O(1), hvis vi ikke overvejer stakstørrelsen for funktionskald. Ellers er pladskompleksiteten af inordergennemgang O(h), hvor 'h' er højden af træet.
Implementering af Inorder traversal
Lad os nu se implementeringen af inorder traversal i forskellige programmeringssprog.
Program: Skriv et program til at implementere in-order traversal i C-sprog.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Produktion

Program: Skriv et program til at implementere inorder traversal i C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Produktion

Program: Skriv et program til at implementere inorder traversal i Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Produktion

Så det handler om artiklen. Håber artiklen vil være nyttig og informativ for dig.











