Overfladeareal af et prisme: I matematik er et prisme et væsentligt medlem af polyederfamilien og er defineret som en tredimensionel form med to identiske polygoner, der vender mod hinanden, og som er forbundet med rektangulære eller parallelogramflader sideværts. De identiske polygoner kan være trekanter, firkanter, rektangler, femkanter eller en hvilken som helst anden n-sidet polygon og kaldes prismets baser. De andre flader af et prisme er parallellogrammer eller rektangler.

I denne artikel vil vi diskutere forskellige typer prismer, og overfladearealet af prismeformlen, med eksempler og praksisproblemer.

Indholdsfortegnelse

• Hvad er overfladearealet af prisme?
• Forskellige typer prismer
• Trekantet prisme
• Rektangulær prisme
• Firkantet prisme
• Femkantet prisme
• Sekskantet prisme
• Prismeformlens overfladeareal
• Overfladeareal af et prisme løst eksempler
• Øv problemer på overfladearealet af et prisme

Hvad er overfladearealet af prisme?

Overfladearealet af et prisme omtales som det samlede areal omgivet af alle dets flader. For at bestemme et prismes overfladeareal skal vi beregne arealerne af hver af dets flader og derefter tilføje de resulterende områder. Et prisme har to slags overfladearealer, nemlig det laterale overfladeareal og det samlede overfladeareal. Området optaget af et prismes flader, eksklusive de to parallelle flader (baser af et prisme), omtales som dets laterale overfladeareal.

Det laterale overfladeareal af et prisme = [Base perimeter × højde] kvadratenheder

Nu er et prismes samlede overfladeareal summen af ​​arealerne af dets to baser og dets laterale overfladeareal.

Den generelle formel til beregning af det samlede overfladeareal af enhver type højre prisme er:

Det samlede overfladeareal af et prisme = [2 (basisareal) + (basisomkreds × højde)] kvadratenheder

Forskellige typer prismer

Der findes forskellige typer prismer baseret på formen på bunden af ​​et prisme, som f.eks

• Trekantede prismer,
• Firkantede prismer,
• rektangulære prismer,
• femkantede prismer,
• Sekskantede prismer,
• Ottekantede prismer.

Trekantet prisme

Et prisme med en trekantet base kaldes et trekantet prisme. Et trekantet prisme består af tre skrå rektangulære overflader og to parallelle trekantbaser. Lad H være højden af ​​det trekantede prisme; a, b og c er sidernes længder, og h er højden af ​​de trekantede baser.

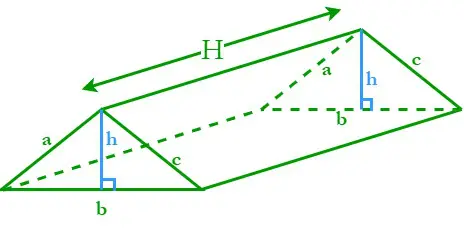
Omkredsen af ​​en trekantet base (P) = Summen af ​​dens tre sider = a + b + c

Arealet af en trekantet base (A) = ½ × base × højde = ½ bh

Vi ved, at den generelle formel for lateral overfladeareal af et højre prisme er L. S. A. = PH, hvor P er basisomkredsen, og A er basisarealet.

Ved at erstatte alle værdierne i den generelle formel får vi ,

Det laterale overfladeareal af et trekantet prisme = (a + b +c)H kvadratenheder

hvor,

a, b, c er sider af trekantet base

H er højden af ​​det trekantede prisme

række af strukturer i c-sprog

Vi ved, at den generelle formel for det samlede overfladeareal af et ret prisme er T. S. A. = PH+2A, hvor P er basisomkredsen, A er basisarealet, og H er prismets højde.

Ved at erstatte alle værdierne i den generelle formel får vi

Det samlede overfladeareal af det trekantede prisme = (a + b + c)H + 2 × (½ bh)

Det samlede overfladeareal af det trekantede prisme = (a + b + c)H + bh kvadratenheder

hvor,

a, b, c er sider af trekantet base

H er højden af ​​det trekantede prisme

h er højden af ​​trekanten

Rektangulær prisme

Et prisme med en rektangulær base omtales som et rektangulært prisme. Et rektangulært prisme består af fire rektangulære overflader og to parallelle rektangulære baser. Lad prismets højde være h og dets rektangulære basers længde og bredde være henholdsvis l og w .

Omkredsen af ​​en rektangulær base (P) = Summen af ​​dens fire sider = 2 (l + w)

Arealet af en rektangulær base (A) = længde × bredde = l × w

Vi ved, at den generelle formel for det laterale overfladeareal af et ret prisme er L. S. A. = PH, hvor P er basisomkredsen, og A er basisarealet.

Ved at erstatte alle værdierne i den generelle formel får vi ,

Det laterale overfladeareal af et rektangulært prisme = 2h(l + w) kvadratenheder

hvor,

l er længde

w er bredde

h er højden

Vi ved, at den generelle formel for det samlede overfladeareal af et ret prisme er T. S. A. = PH+2A, hvor P er basisomkredsen, A er grundarealet, og H er prismets højde.

Ved at erstatte alle værdierne i den generelle formel får vi

Det totale overfladeareal af det rektangulære prisme = 2h(l + w) + 2(l × w)

= 2 lh + 2 wh + 2 lw

Det totale overfladeareal af det rektangulære prisme = 2 (lh + wh + lw) kvadratenheder

hvor,

l er længde

w er bredde

h er højden

Firkantet prisme

Et prisme med en kvadratisk base kaldes et kvadratisk prisme. Et kvadratisk prisme består af fire rektangulære overflader og to parallelle kvadratiske baser. Lad prismets højde være h og dets kvadratiske basers længder være s.

Omkredsen af ​​en kvadratisk base (P) = Summen af ​​dens fire sider = s + s + s + s = 4s

Arealet af en kvadratisk base (A) = (længden af ​​siden)²= s²

Vi ved, at den generelle formel for det laterale overfladeareal af et ret prisme er L. S. A. = PH, hvor P er basisomkredsen, og A er basisarealet.

Ved at erstatte alle værdierne i den generelle formel får vi,

Det laterale overfladeareal af et kvadratisk prisme = 4sh kvadratenheder

hvor,

s er siden af ​​kvadratisk base

h er højden af ​​kvadratisk prisme

Vi ved, at den generelle formel for det samlede overfladeareal af et ret prisme er T.S.A. = PH+2A, hvor P er basisomkredsen, A er basisarealet, og H er prismets højde.

Ved at erstatte alle værdierne i den generelle formel får vi

Det totale overfladeareal af det kvadratiske prisme = [4sh + 2s ² ] kvadratenheder

hvor,

s er siden af ​​kvadratisk base

h er højden af ​​kvadratisk prisme

Femkantet prisme

Et prisme med en femkantet base omtales som et femkantet prisme. Et femkantet prisme består af fem skrå rektangulære overflader og to parallelle femkantede baser. Lad h være højden af ​​det femkantede prisme; a og b er apotemlængden og sidelængden af ​​de femkantede baser.

Omkredsen af ​​en femkantet base (P) = Summen af ​​dens fem sider = 5b

Arealet af en femkantet base (A) = 5/2 x (apotem længde) x (længde af siden) = 5ab

Vi ved, at den generelle formel for det laterale overfladeareal af et ret prisme er L. S. A. = PH, hvor P er basisomkredsen, og A er basisarealet.

Ved at erstatte alle værdierne i den generelle formel får vi,

Det laterale overfladeareal af et femkantet prisme = 5bh kvadratenheder

hvor,

b er siden af ​​femkantet base

h er højden af ​​femkantet prisme

Vi ved, at den generelle formel for det samlede overfladeareal af et ret prisme er T. S. A. = PH+2A, hvor P er basisomkredsen, A er grundarealet, og H er prismets højde.

Ved at erstatte alle værdierne i den generelle formel får vi,

Det samlede overfladeareal af det femkantede prisme = [5bh + 5ab] kvadratenheder

hvor,

b er siden af ​​femkantet base

a er apotemlængde.

h er højden af ​​femkantet prisme

Sekskantet prisme

Et prisme med en sekskantet base omtales som et sekskantet prisme. Et sekskantet prisme består af seks skrå rektangulære overflader og to parallelle sekskantede baser. Lad h være højden af ​​det sekskantede prisme; a være sidelængderne af de sekskantede baser.

Omkredsen af ​​en sekskantbase (P) = Summen af ​​dens seks sider = 6a

Arealet af en sekskantet base (A) = 6 x (arealet af en ligesidet trekant)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Vi ved, at den generelle formel for det laterale overfladeareal af et ret prisme er L. S. A. = PH, hvor P er basisomkredsen, og A er basisarealet.

Ved at erstatte alle værdierne i den generelle formel får vi,

Det laterale overfladeareal af et sekskantet prisme = 6ah kvadratenheder

hvor,

a er siden af ​​sekskantet base

h er højden af ​​den sekskantede base

Vi ved, at den generelle formel for det samlede overfladeareal af et ret prisme er T. S. A. = PH+2A, hvor P er basisomkredsen, A er grundarealet, og H er prismets højde.

Ved at erstatte alle værdierne i den generelle formel får vi

Det totale overfladeareal af det sekskantede prisme = [6ah +3√3a²] kvadratenheder

hvor,

a er siden af ​​sekskantet base

numpy linspace

h er højden af ​​den sekskantede base:

Prismeformlens overfladeareal

Tabellen nedenfor giver formlen for forskellige typer prismer:

Overfladeareal af et prisme løst eksempler

Opgave 1: Hvad er højden af ​​et prisme, hvis grundareal er 36 kvadratenheder, dets grundomkreds er 24 enheder, og dets samlede overfladeareal er 320 kvadratenheder?

Løsning:

Givet data,

Basisareal = 36 kvadratenheder

Basisomkreds = 24 enheder

Prismets samlede overfladeareal = 320 kvadratenheder

Vi har,

Prismets samlede overfladeareal = (2 × basisareal) + (basisomkreds × højde)

⇒ 320 = (2 × 36)+ (24 × t)

⇒ 24 timer = 248 ⇒ t = 10,34 enheder

Derfor er højden af ​​det givne prisme 10,34 enheder.

Opgave 2: Find det samlede overfladeareal af et kvadratisk prisme, hvis højden af ​​prismet og længden af ​​siden af ​​kvadratbunden er henholdsvis 13 cm og 4 cm.

Løsning:

Givet data,

Højden af ​​det firkantede prisme (h) = 13 cm

Længden af ​​siden af ​​den firkantede base (a) = 4 cm

Vi ved det,

Det samlede overfladeareal af et kvadratisk prisme = 2a²+ 4ah

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Derfor er det samlede overfladeareal af det givne prisme 240 cm2.

Opgave 3: Bestem grundlængden af ​​et femkantet prisme, hvis dets samlede areal er 100 kvadratenheder og dets højde og apotemlængde er henholdsvis 8 enheder og 5 enheder.

Løsning:

Givet data,

Det samlede overfladeareal af det femkantede prisme = 100 kvadratenheder

Prismets højde (h) = 8 enheder

Apotemlængde (a) = 5 enheder

Vi ved det,

Det samlede overfladeareal af det femkantede prisme = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 enheder

Derfor er basislængden 1,54 enheder

Opgave 4: Bestem højden af ​​det rektangulære prisme og det samlede areal af et rektangulært prisme, hvis dets laterale overfladeareal er 540 sq. cm og længden og bredden af ​​basen er henholdsvis 13 cm og 7 cm.

Løsning:

Givet data,

Længden af ​​den rektangulære base (l) = 13 cm

Bredden af ​​den rektangulære base (b) = 7 cm

Prismets laterale overfladeareal = 540 cm2

Vi har,

Prismets laterale overfladeareal = Baseomkreds × højde

⇒ 540 = 2 (l + w) h

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) t = 540 ⇒ t = 13,5 cm

Vi ved det,

Det totale overfladeareal af det rektangulære prisme = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 cm2

Derfor er højden og det samlede overfladeareal af det givne rektangulære prisme henholdsvis 13,5 cm og 722 cm2.

Opgave 5: Bestem overfladearealet af det regulære sekskantede prisme, hvis højden af ​​prismet er 12 tommer og længden af ​​siden af ​​basen er 5 tommer.

Løsning:

Givet data,

Prismets højde (h) = 12 tommer

Længden af ​​siden af ​​basen (a) = 6 tommer

Overfladearealet af et regulært sekskantet prisme = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 sq. in

Derfor er overfladearealet af det givne prisme 489,9 sq. in.

Opgave 6: Beregn de laterale og samlede overfladearealer af et trekantet prisme, hvis basisomkreds er 25 tommer, trekantens basislængde og højde er 9 tommer og 10 tommer, og prismets højde er 14 tommer.

Løsning:

Givet data,

Prismets højde (H) = 14 tommer

Prismets grundomkreds (P) = 25 tommer

Basislængden af ​​trekanten = 9 tommer

Højden af ​​trekanten = 10 tommer

Vi ved det,

Prismets laterale overfladeareal = Baseomkreds × højde

= 25 × 14= 350 sq. in

Charat i streng

Areal af den trekantede base (A) = ½ × base × højde = 1/2 × 9 × 10 = 45 sq. in

Det samlede overfladeareal af det trekantede prisme = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 sq. in

Derfor er prismets laterale og samlede overfladearealer henholdsvis 350 sq. in og 440 sq. in.

Øv problemer på overfladearealet af et prisme

1. Givet et rektangulært prisme med dimensioner:

• Længde = 6 cm
• Bredde = 4 cm
• Højde = 5 cm

Beregn det samlede overfladeareal.

2. Overvej et trekantet prisme med dimensioner:

• Trekantens bund = 8 cm
• Trekantens højde = 6 cm
• Prismets længde = 10 cm

Find det samlede overfladeareal.

3. Bestem overfladearealet af et regulært femkantet prisme med:

• Sidelængde af basen = 7 cm
• Prismets højde = 9 cm.

4. Beregn overfladearealet af et sekskantet prisme med:

• Sidelængde af den regulære sekskantede base = 10 cm
• Prismets højde = 12 cm.

Overfladeareal af et prisme – ofte stillede spørgsmål

Hvad er et prisme i geometri?

Et prisme er en tredimensionel form med to kongruente parallelle baser og rektangulære eller parallelogram laterale flader, der forbinder dem. Prismer kommer i forskellige former, såsom rektangulære prismer, trekantede prismer og femkantede prismer, hver med unikke egenskaber.

Hvordan finder du overfladearealet af et prisme?

For at finde overfladearealet af et prisme skal du beregne arealerne af alle dets flader og derefter summere dem. For et rektangulært prisme er overfladearealformlen 2lw + 2lh + 2wh, hvor l er længden, w er bredden og h er højden. For andre typer prismer, såsom trekantede eller femkantede prismer, kan der være behov for yderligere formler for basisareal og sideareal.

Hvad er egenskaberne ved et prisme?

Prismer har flere nøgleegenskaber:

• De har to kongruente parallelle baser.
• Sidefladerne er alle parallelogrammer.
• Højden (højden) er den vinkelrette afstand mellem de to baser.
• Basene er identiske i form og størrelse.
• Tværsnittet parallelt med bunden har altid samme form og størrelse som bunden.

Hvad er nogle eksempler fra det virkelige liv på prismer?

Prismer kan findes i forskellige hverdagsgenstande og strukturer. Eksempler omfatter:

• Rektangulære prismer: Bygninger, kornkasser, bøger.
• Trekantede prismer: Tage på huse, kileformede genstande.
• Femkantede prismer: Nogle typer søjler, visse arkitektoniske strukturer.
• Sekskantede prismer: Visse typer krystaller, nogle emballagebeholdere.

Hvorfor er overfladeareal vigtigt i prismer?

Overfladeareal er afgørende i prismer, da det repræsenterer det samlede areal af alle prismets overflader (flader). Forståelse af overfladearealet hjælper med forskellige praktiske anvendelser, såsom at beregne mængden af ​​materiale, der er nødvendigt for at bygge eller dække et prismeformet objekt, bestemme varmeoverførselshastigheder og optimere emballagedesign.