En cirkel består af punkter, der alle er i samme afstand fra cirklens centrum. En lukket geometrisk form er en cirkel. I hverdagen ser vi cirkler i form af et hjul, pizzaer, en rund jord og så videre.

Dele af en cirkel

Nøglebegreber:

hvad er ymail

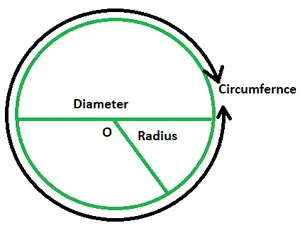
• Radius: Det radius af en cirkel er afstanden mellem dets centrum og ethvert punkt på kanten. Det er generelt betegnet som r. En cirkel har et uendeligt antal radier.
• Diameter: Det er en linje, der løber gennem midten og har sine ender på cirklen. Det er betegnet som D og er det dobbelte af værdien af ​​cirklens radius.
• Omkreds: Udstrækningen af ​​cirklens grænse svarer til dens omkreds. Dette betyder, at en cirkels omkreds er lig med dens omkreds. Cirklens omkreds vil være lig med længden af ​​tråden, der pænt vikler rundt om dens omkreds. Det er givet som 2πr.

Hvad er cirkelområdet?

Arealet af en cirkel er relateret til mængden af ​​rum, der er omfattet af en cirkels kant. Området udfyldt af cirklen er territoriet inden for cirklens omkreds. Det er også kendt som det samlede antal kvadratenheder inkluderet i cirklen.

Kontrollere: Diameter af en cirkel

Område med cirkelformler

Overfladearealet af en cirkel er givet ved følgende formel:

A = πr ²

hvor r er radius af den givne cirkel.

eller

A = C ² /4p

hvor C er omkredsen af ​​den givne cirkel.

Eksempler på formlen for Cirkelareal

Spørgsmål 1. Find arealet af en cirkel givet dens radius er 8 m.

Løsning:

Givet: r = 8 m

Da arealet af en cirkel = πr²

A = π(8)²

= 64p

= 200,96 m ²

Spørgsmål 2. Find arealet af en cirkel givet dens omkreds er 12 cm.

Løsning:

Givet: C = 12 cm

indsættelsessorteringsalgoritmer

Da A = C²/4p

= 12²/4p

= 11,46 cm ²

Spørgsmål 3. Find arealet af en cirkel givet dens diameter er 12 cm.

Løsning:

Givet: D = 12 cm

eller, Radius = r = 12/2 = 6 cm

Da A = πr²

= π(6)2

= 113,04 cm ²

Spørgsmål 4. Find arealet af en cirkel givet dens radius er 9 cm.

Løsning:

Givet: r = 9 m

Da arealet af en cirkel = πr²

A = π(9)²

binær træpostordregennemgang

= 81p

= 254,34 cm ²

Spørgsmål 5. Find arealet af en cirkel givet dens diameter er 10 cm.

Løsning:

Givet: D = 10 cm

eller, Radius = r = 10/2 = 5 cm

Da A = πr²

= π(5)²

= 78,5 cm ²

Tjek også:

• Areal Af En Cirkel Lommeregner
• Kvadratoptagelser af Circle Calculator
• Radius Af En Cirkel Lommeregner
• Diameter af en cirkelberegner
• Omkreds Lommeregner
• Omkreds til Diameter Lommeregner