Givet en BST , opgaven er at søge en node i denne BST .
For at søge efter en værdi i BST skal du betragte den som et sorteret array. Nu kan vi nemt udføre søgeoperation i BST ved hjælp af Binær søgealgoritme .
Algoritme til at søge efter en nøgle i et givet binært søgetræ:
Lad os sige, at vi vil søge efter nummeret X, Vi starter ved roden. Derefter:
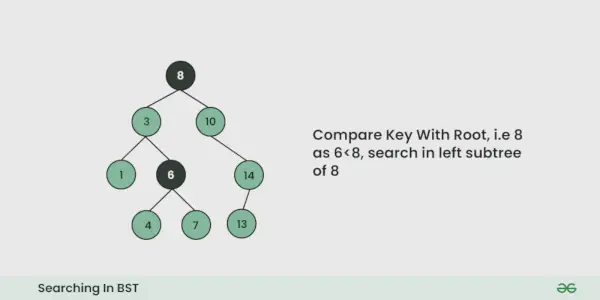
- Vi sammenligner den værdi, der skal søges i, med værdien af roden.
- Hvis det er ens, er vi færdige med søgningen, hvis den er mindre, ved vi, at vi skal gå til venstre undertræ, fordi i et binært søgetræ er alle elementerne i venstre undertræ mindre, og alle elementerne i det højre undertræ er større.
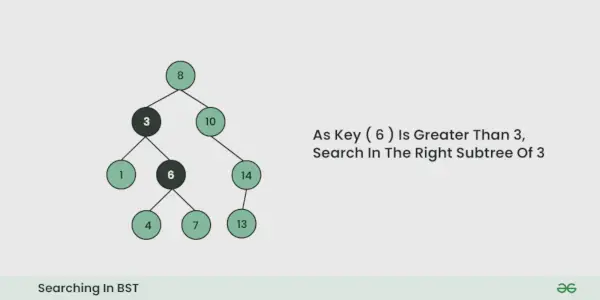
- Gentag ovenstående trin, indtil det ikke er muligt at krydse mere
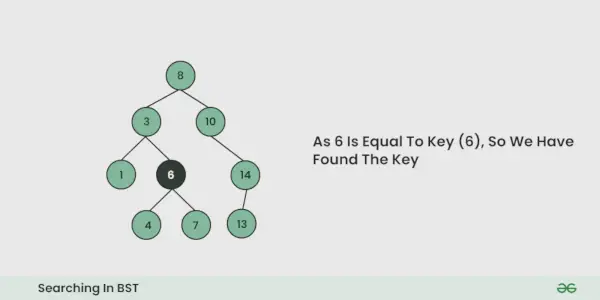
- Hvis nøglen findes ved en gentagelse, returneres True. Ellers falsk.
Illustration af søgning i en BST:
Se illustrationen nedenfor for en bedre forståelse:
Anbefalet praksisSøg efter en node i BSTTry It!
Program til at implementere søgning i BST:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >=>new> struct> node;> >temp->nøgle = element;> >temp->venstre = temp->højre = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->venstre = indsæt(node->venstre, tast);> >else> if> (key>node->tast)> >node->højre = indsæt(node->højre, nøgle);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > >// Base Cases: root is null or key is present at root> >if> (root == NULL> // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >return> 0;> }> |
>
>
C
// C function to search a given key in a given BST> #include> #include> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >= (>struct> node*)>malloc>(>sizeof>(>struct> node));> >temp->nøgle = element;> >temp->venstre = temp->højre = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->venstre = indsæt(node->venstre, tast);> >else> if> (key>node->tast)> >node->højre = indsæt(node->højre, nøgle);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >return> 0;> }> |
>
find min iphone fra Android
>
Java
// Java program to search a given key in a given BST> class> Node {> >int> key;> >Node left, right;> >public> Node(>int> item) {> >key = item;> >left = right =>null>;> >}> }> class> BinarySearchTree {> >Node root;> >// Constructor> >BinarySearchTree() {> >root =>null>;> >}> >// A utility function to insert> >// a new node with given key in BST> >Node insert(Node node,>int> key) {> >// If the tree is empty, return a new node> >if> (node ==>null>) {> >node =>new> Node(key);> >return> node;> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); // Returner (uændret) node pointer return node; } // Hjælpefunktion til at søge efter en nøgle i en BST Node-søgning(Node root, int key) // Driver Code public static void main(String[] args) { BinarySearchTree tree = new BinarySearchTree(); // Indsættelse af noder tree.root = tree.insert(tree.root, 50); tree.insert(tree.root, 30); træ.indsæt(træ.rod, 20); træ.indsæt(træ.rod, 40); træ.indsæt(træ.rod, 70); træ.indsæt(træ.rod, 60); træ.indsæt(træ.rod, 80); // Nøgle der skal findes int nøgle = 6; // Søger i en BST if (tree.search(tree.root, key) == null) System.out.println(key + ' ikke fundet'); else System.out.println(tast + ' fundet'); nøgle = 60; // Søger i en BST if (tree.search(tree.root, key) == null) System.out.println(key + ' ikke fundet'); else System.out.println(tast + ' fundet'); } }> |
>
>
Python3
# Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Returner (uændret) node pointer return node # Utility funktion til at søge efter en nøgle i en BST def search(root, key): # Basistilfælde: root er null eller nøgle er til stede ved root, hvis root er Ingen eller root.key == nøgle: returner root # Key er større end roots nøgle hvis root.key returner søgning(root.right, key) # Key er mindre end root 's nøgle returner søgning(root.left, key) # Driverkode hvis __navn__ == '__main__': root = Ingen root = insert(root, 50) insert(root, 30) insert(root, 20) insert (rod, 40) insert(root, 70) insert(root, 60) insert(root, 80) # Nøgle, der skal findes nøgle = 6 # Søger i en BST, hvis søgning(rod, nøgle) er Ingen: print(nøgle, 'ikke fundet') andet: print(nøgle, 'fundet') nøgle = 60 # Søger i en BST, hvis søgning (rod, nøgle) er Ingen: print(nøgle, 'ikke fundet') andet: print(nøgle, 'fundet')> |
>
>
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key node.left = Insert(node.left, key); else if (key>node.key) node.right = Indsæt(node.højre, nøgle); // Returner (uændret) node pointer return node; } // Utility-funktion til at søge efter en nøgle i en BST offentlig nodesøgning(Node-rod, int-nøgle) // Base Cases: root er null eller nøgle er til stede ved root if (root == null // Driver Code public static void Main () { Node root = null BinaryTree bt = new BinaryTree(); , 40); bt.Insert(root, 70).Insert(root, 80); bt.Search(root, key) == null) Console.WriteLine(nøgle + ' ikke fundet'); if (bt.Search(root, key) == null) Console.WriteLine(nøgle + ' ikke fundet'); |
streng til tegn
>
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner den (uændrede) node pointer return node; } // Hjælpefunktion til at søge efter en nøgle i en BST-funktionssøgning(root, key) { // Grundtilfælde: root er null eller nøgle er til stede ved root if (root === null || root.key === nøgle ) { returner rod; } // Nøglen er større end roots nøgle if (root.key returner søgning(root.right, key); } // Nøglen er mindre end roots nøgle return søgning(root.left, key); } // Driver Code let root = insert(root, 30 insert(root, 40); 60); insert(root, 80); // Key to be found let key = 6; // Søger i en BST if (søg(rod, nøgle) === null) found'); } else { console.log(key + ' found' } key = 60; Søger i en BST if (search(root, key) tast + ' ikke fundet'); } else { console.log(tast + ' fundet' }>>>Produktion6 not found 60 found>Tidskompleksitet: O(h), hvor h er højden af BST.
Hjælpeplads: O(h), hvor h er højden af BST. Dette skyldes, at den maksimale mængde plads, der er nødvendig for at opbevare rekursionsstakken, ville være h .Relaterede links:
- Binær søgetræindsættelsesoperation
- Binær søgetræ Slet operation