Kvantil-kvantil (q-q plot) plot er en grafisk metode til at bestemme, om et datasæt følger en bestemt sandsynlighedsfordeling, eller om to stikprøver af data kom fra samme befolkning eller ikke. Q-Q plots er særligt nyttige til at vurdere, om et datasæt er normalt fordelt eller hvis den følger en anden kendt fordeling. De bruges almindeligvis i statistik, dataanalyse og kvalitetskontrol til at kontrollere antagelser og identificere afvigelser fra forventede fordelinger.
Kvantiler Og Percentiler
Kvantiler er punkter i et datasæt, der opdeler dataene i intervaller, der indeholder lige store sandsynligheder eller proportioner af den samlede fordeling. De bruges ofte til at beskrive spredningen eller distributionen af et datasæt. De mest almindelige kvantiler er:
- Median (50. percentil) : Medianen er den midterste værdi af et datasæt, når det er sorteret fra mindste til største. Den deler datasættet i to lige store halvdele.
- Kvartiler (25., 50. og 75. percentil) : Kvartiler deler datasættet i fire lige store dele. Den første kvartil (Q1) er den værdi, under hvilken 25 % af dataene falder, den anden kvartil (Q2) er medianen, og den tredje kvartil (Q3) er den værdi, hvorunder 75 % af dataene falder.
- Percentiler : Percentiler ligner kvartiler, men opdeler datasættet i 100 lige store dele. For eksempel er 90. percentilen den værdi, som 90 % af dataene falder under.
Bemærk:
- Et q-q plot er et plot af kvantiler af det første datasæt mod kvantiler af det andet datasæt.
- Til referenceformål er der også plottet en 45% linje; Til hvis prøverne er fra den samme population, er punkterne langs denne linje.
Normal fordeling:
Normalfordelingen (også kaldet Gauss-fordelingsklokkekurve) er en kontinuerlig sandsynlighedsfordeling, der repræsenterer fordelingen opnået fra de tilfældigt genererede reelle værdier.
. 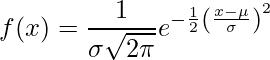

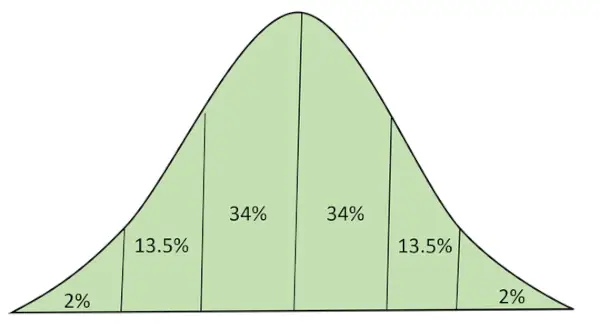
Normalfordeling med areal under kurve
Hvordan tegner man Q-Q plot?
For at tegne et Quantile-Quantile (Q-Q) plot kan du følge disse trin:
- Indsaml data : Saml det datasæt, som du vil oprette Q-Q-plotten for. Sørg for, at dataene er numeriske og repræsenterer en tilfældig stikprøve fra populationen af interesse.
- Sorter dataene : Arranger dataene i enten stigende eller faldende rækkefølge. Dette trin er afgørende for at beregne kvantiler nøjagtigt.
- Vælg en teoretisk fordeling : Bestem den teoretiske fordeling, som du vil sammenligne dit datasæt med. Almindelige valg omfatter normalfordelingen, eksponentiel fordeling eller enhver anden fordeling, der passer godt til dine data.
- Beregn teoretiske kvantiler : Beregn kvantiler for den valgte teoretiske fordeling. Hvis du for eksempel sammenligner med en normalfordeling, vil du bruge den inverse kumulative distributionsfunktion (CDF) af normalfordelingen til at finde de forventede kvantiler.
- Plotning :
- Plot de sorterede datasætværdier på x-aksen.
- Plot de tilsvarende teoretiske kvantiler på y-aksen.
- Hvert datapunkt (x, y) repræsenterer et par observerede og forventede værdier.
- Forbind datapunkterne for visuelt at inspicere forholdet mellem datasættet og den teoretiske fordeling.
Fortolkning af Q-Q plot
- Hvis punkterne på plottet falder nogenlunde langs en ret linje, tyder det på, at dit datasæt følger den forudsatte fordeling.
- Afvigelser fra den rette linje indikerer afvigelser fra den forudsatte fordeling, hvilket kræver nærmere undersøgelse.
Udforsker distributionslighed med Q-Q-plot
At udforske distributionslighed ved hjælp af Q-Q plots er en grundlæggende opgave i statistik. Sammenligning af to datasæt for at bestemme, om de stammer fra den samme distribution, er afgørende for forskellige analytiske formål. Når antagelsen om en fælles fordeling holder, kan fletning af datasæt forbedre parameterestimeringsnøjagtigheden, såsom for placering og skala. Q-Q plots, forkortelse for quantile-quantile plots, tilbyder en visuel metode til at vurdere distributionslighed. I disse plots plottes kvantiler fra ét datasæt mod kvantiler fra et andet. Hvis punkterne er tæt på linje langs en diagonal linje, tyder det på lighed mellem fordelingerne. Afvigelser fra denne diagonale linje indikerer forskelle i fordelingsegenskaber.
Mens tests som chi-kvadrat og Kolmogorov-Smirnov test kan evaluere overordnede distributionsforskelle, Q-Q plots giver et nuanceret perspektiv ved direkte at sammenligne kvantiler. Dette gør det muligt for analytikere at skelne specifikke forskelle, såsom skift i placering eller ændringer i skala, som måske ikke er tydelige fra formelle statistiske test alene.
Python-implementering af Q-Q-plot
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Produktion:
Q-Q plot
Her, da datapunkterne tilnærmelsesvis følger en ret linje i Q-Q plottet, tyder det på, at datasættet stemmer overens med den forudsatte teoretiske fordeling, som vi i dette tilfælde antog for at være normalfordelingen.
Fordele ved Q-Q plot
- Fleksibel sammenligning : Q-Q plots kan sammenligne datasæt af forskellige størrelser uden kræver lige store stikprøvestørrelser.
- Dimensionsløs analyse : De er dimensionsløse, hvilket gør dem velegnede til at sammenligne datasæt med forskellige enheder eller skalaer.
- Visuel fortolkning : Giver en klar visuel repræsentation af datadistribution sammenlignet med en teoretisk distribution.
- Følsom over for afvigelser : Registrerer nemt afvigelser fra antagne distributioner, hvilket hjælper med at identificere dataafvigelser.
- Diagnostisk værktøj : Hjælper med at vurdere fordelingsantagelser, identificere outliers og forstå datamønstre.
Anvendelser af kvantil-kvantile plot
Quantile-Quantile plottet bruges til følgende formål:
- Vurdering af fordelingsantagelser : Q-Q plots bruges ofte til visuelt at inspicere, om et datasæt følger en specifik sandsynlighedsfordeling, såsom normalfordelingen. Ved at sammenligne kvantiler af de observerede data med kvantiler af den antagne fordeling kan afvigelser fra den antagne fordeling påvises. Dette er afgørende i mange statistiske analyser, hvor gyldigheden af fordelingsantagelser påvirker nøjagtigheden af statistiske slutninger.
- Opdagelse af outliers : Outliers er datapunkter, der afviger væsentligt fra resten af datasættet. Q-Q plots kan hjælpe med at identificere outliers ved at afsløre datapunkter, der falder langt fra det forventede mønster af fordelingen. Outliers kan forekomme som punkter, der afviger fra den forventede rette linje i plottet.
- Sammenligning af distributioner : Q-Q plots kan bruges til at sammenligne to datasæt for at se, om de kommer fra den samme distribution. Dette opnås ved at plotte kvantiler af et datasæt mod kvantiler af et andet datasæt. Hvis punkterne falder tilnærmelsesvis langs en ret linje, tyder det på, at de to datasæt er trukket fra den samme fordeling.
- Vurdere normalitet : Q-Q plots er særligt nyttige til at vurdere normaliteten af et datasæt. Hvis datapunkterne i plottet nøje følger en ret linje, indikerer det, at datasættet er tilnærmelsesvis normalfordelt. Afvigelser fra linjen tyder på afvigelser fra normalitet, hvilket kan kræve yderligere undersøgelse eller ikke-parametriske statistiske teknikker.
- Modelvalidering : I felter som økonometri og maskinlæring bruges Q-Q-plot til at validere forudsigende modeller. Ved at sammenligne kvantiler af observerede responser med kvantiler forudsagt af en model, kan man vurdere, hvor godt modellen passer til dataene. Afvigelser fra det forventede mønster kan indikere områder, hvor modellen skal forbedres.
- Kvalitetskontrol : Q-Q plots anvendes i kvalitetskontrolprocesser til at overvåge fordelingen af målte eller observerede værdier over tid eller på tværs af forskellige batches. Afvigelser fra forventede mønstre i plottet kan signalere ændringer i de underliggende processer, hvilket foranlediger yderligere undersøgelser.
Typer af Q-Q plots
Der er flere typer Q-Q-plot, der almindeligvis bruges i statistik og dataanalyse, hver egnet til forskellige scenarier eller formål:
- Normal fordeling : En symmetrisk fordeling, hvor Q-Q-plottet ville vise punkter omtrent langs en diagonal linje, hvis dataene overholder en normalfordeling.
- Højreskæv Fordeling : En fordeling, hvor Q-Q plottet ville vise et mønster, hvor de observerede kvantiler afviger fra den lige linje mod den øvre ende, hvilket indikerer en længere hale på højre side.
- Venstreskæv Fordeling : En fordeling, hvor Q-Q plottet ville udvise et mønster, hvor de observerede kvantiler afviger fra den lige linje mod den nederste ende, hvilket indikerer en længere hale på venstre side.
- Underfordelt distribution : En fordeling, hvor Q-Q-plottet ville vise observerede kvantiler samlet tættere omkring den diagonale linje sammenlignet med de teoretiske kvantiler, hvilket tyder på lavere varians.
- Overspredning : En fordeling, hvor Q-Q-plottet ville vise observerede kvantiler mere spredt ud eller afvigende fra den diagonale linje, hvilket indikerer højere varians eller dispersion sammenlignet med den teoretiske fordeling.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Produktion:
Q-Q plot til forskellige distributioner
streng java indexof
