Inertimoment er egenskaben for et legeme i rotationsbevægelse. Inertimoment er rotationslegemernes egenskab, som har en tendens til at modsætte sig ændringen i kroppens rotationsbevægelse. Det ligner inertien af ethvert legeme i translationel bevægelse. Matematisk er inertimomentet givet som summen af produktet af massen af hver partikel og kvadratet af afstanden fra rotationsaksen. Det måles i enheden af kgm 2 .
Lad os lære om inertiamomentet i detaljer i artiklen nedenfor.
Indholdsfortegnelse
- Definition af inertimoment
- Formel for inertimoment
- Faktorer, der påvirker inertimomentet
- Hvordan beregner man inertimoment?
- Moment Of Inertia Formel for forskellige former
- Gyrationsradius
- Inertimomentsætninger
- Inertimomenter for forskellige objekter
Definition af inertimoment
Inertimoment er tendensen hos et legeme i rotationsbevægelse, som modarbejder ændringen i dets roterende bevægelse på grund af ydre kræfter. Inertimomentet opfører sig som vinkelmasse og kaldes rotationsinerti. Inertimoment er analogt med det mekaniske Træghed af kroppen.
MOI er defineret som mængden udtrykt ved summen af produktet af masse af hver partikel med kvadratet på dens afstand fra rotationsaksen for enhver partikel, der udfører rotationsbevægelsen.
Enhed for inertimoment
Inertimoment er en skalær størrelse, og SI-enheden for inertimomentet er kgm 2 .
Inertia Moment of Inertia Dimensional Formula
Da inertimomentet er givet som produktet af masse og kvadrat af afstand. Dens dimensionel formel er givet ved produktet af dimensionsformlen for masse og kvadratet af dimensionsformlen for længde. Den dimensionelle formel for inertimomentet er, ML 2
Hvad er inerti?
Træghed er egenskaben af et stof, i kraft af hvilket det har en tendens til at modstå ændringen i dets bevægelsestilstand. Dette betyder, at en krop i hvile forsøger at forblive i hvile og modstå enhver kraft, der prøver at bringe den i bevægelse, og en krop i bevægelse forsøger at fortsætte i bevægelse og modstå enhver kraft, der forsøger at få den til at ændre størrelsen af dens bevægelse. Med hensyn til mængde er det lig med den maksimale kraft, der forsøger at ændre sin tilstand af bevægelse .
Lær mere om Træghed .
Formel for inertimoment
Inertimomentet er et skalær mængde . Matematisk kaldes produktet af kvadratet af en partikels masse og afstanden fra omdrejningsaksen for partiklens inertimoment omkring rotationsaksen.
Den generelle formel for at finde inertimomentet for ethvert objekt er,
jeg = hr 2
hvor,
m er massen af objektet'
r er afstanden fra rotationsaksen
For et legeme, der består af kontinuerlige uendeligt små partikler, bruges den integrale form af inertimomentet til at beregne inertimomentet.
I = ∫dI
jeg =
int_{0}^{M} r^2 dm
Inertimoment af et system af partikler
Inertimoment af et system af partikler er givet ved formlen,
I = ∑m jeg r jeg 2
hvor,
r jeg er den vinkelrette afstand af i'etthpartikel fra aksen
m jeg er massen af ithpartikel
Ovenstående inertimoment-ligning fortæller, at inertimomentet for et system af partikler er lig med summen af produktet af massen af hver og kvadratet af afstanden fra rotationsaksen for hver partikel.
For figuren nedenfor,
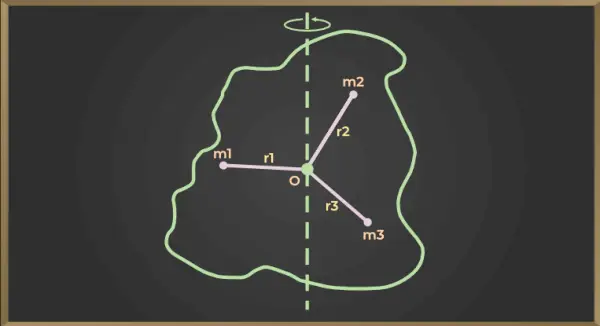
Inertimoment for første partikel = m1×r12
Inertimoment for anden partikel = m2×r22
Tredje partikels inertimoment = m3×r32
Tilsvarende
Inertimoment af nthpartikel = mn×rn2
Nu inertimomentet for hele kroppen omkring rotationsaksen AB vil være lig med summen af inertimomentet for alle partiklerne, så
I = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
linkedlist og arraylist
I = Σm jeg ×r jeg 2
hvor,
jeg repræsenterer kroppens inertimoment omkring rotationsaksen
m jeg er massen af ithpartikel,
r jeg er radius af ithpartikel
S repræsenterer summen.
Ud fra ligningen kan vi sige, at et legemes inertimoment omkring en fast akse er lig med summen af produktet af massen af hver partikel i det legeme og kvadratet af dets vinkelrette afstand fra den faste akse.
Faktorer, der påvirker inertimomentet
Ethvert objekts inertimoment afhænger af følgende værdier:
- Objektets form og størrelse
- Densitet af genstandens materiale
- Rotationsakse
Hvordan beregner man inertimoment?
Flere måder er vant til udregn inertimomentet af enhver roterende genstand.
- For ensartede objekter beregnes inertimomentet ved at tage produktet af dets masse med kvadratet på dets afstand fra rotationsaksen (r)2).
- For ikke-ensartede objekter beregner vi inertimomentet ved at tage summen af produktet af individuelle punktmasser ved hver forskellig radius for dette er den anvendte formel
I = ∑m jeg r jeg 2
Moment Of Inertia Formel for forskellige former
Denne tabel diskuterer udtryk for inertimomentet for nogle symmetriske objekter sammen med deres rotationsakse:

| Objekt | Akse | Udtryk for inertimomentet |
|---|---|---|
| Hulcylinder Tyndvægget | Central | Jeg = Hr2 |
| Tynd Ring | Diameter | I = 1/2 Mr2 |
| Ringformet ring eller hul cylinder | Central | I = 1/2 M(r22+ r12) |
| Solid cylinder | Central | I = 1/2 Mr2 |
| Uniform Disc | Diameter | I = 1/4 Mr2 |
| Hul kugle | Central | I = 2/3 Mr2 |
| Solid Kugle | Central | I = 2/5 Mr2 |
| Ensartet symmetrisk sfærisk skal | Central | |
| Ensartet plade eller rektangulært parallelrør | Central | I = 1/12 M(a2+ b2) |
| Tynd stang | Central | I = 1/12 Mr2 |
| Tynd stang | For enden af Rod | I = 1/3 Mr2 |
Gyrationsradius
Det Gyrationsradius af et legeme defineres som den vinkelrette afstand fra rotationsaksen til massepunktet, hvis masse er lig med hele kroppens masse, og inertimomentet er lig med objektets faktiske inertimoment, som det har været. antaget, at den samlede masse af kroppen er koncentreret der. Det er en imaginær afstand. Gyrationsradius er angivet med K.
Hvis kroppens masse og drejningsradius er henholdsvis M og K, er inertimomentet for et legeme
I = MK 2 ……(1)
Således er et legemes gyrationsradius vinkelret på rotationsaksen, hvis kvadrat ganget med massen af det legeme giver kroppens inertimoment omkring denne akse.
Igen ved ligning (1), K2= I/M
K = √(I/m)
Således er radius af svingningen af et legeme omkring en akse lig med kvadratroden af forholdet mellem kroppen omkring den akse.
Inertimomentsætninger
Der er to typer sætninger, der er meget vigtige med hensyn til inertimomentet:
- Parallelaksesætning
- Perpendikulær aksesætning
Perpendikulær aksesætning
Perpendikulær aksesætning angiver, at summen af inertimomentet for et legeme omkring to indbyrdes vinkelrette akser beliggende i et legemes plan er lig med inertimomentet for legemet omkring den tredje akse, som er vinkelret på de to akser og går gennem deres punkt af kryds.

I ovenstående figur, OKSE og LTD er to akser i kroppens plan, som er vinkelrette på hinanden. Den tredje akse er OZ som er vinkelret på kroppens plan og passerer gennem skæringspunktet mellem OKSE og LTD akser. Hvis jeg x , jeg og , og jeg Med er kroppens inertimomenter omkring aksen OKSE , LTD , og OZ henholdsvis akser, så ifølge denne sætning
reagere inline stil
jeg x + I og = jeg Med
Parallelaksesætning
Ifølge Parallel akse sætning , inertimomentet for et legeme omkring en given akse er summen af inertimomentet om en akse, der går gennem det pågældende legemes massecenter og produktet af kvadratet af kroppens masse og den vinkelrette afstand mellem to akser.

Lad i ovenstående figur, vi er nødt til at finde inertimomentet af jeg O af kroppen, der passerer gennem punktet O og om aksen vinkelret på planet, mens kroppens inertimoment passerer gennem massecentret C og om en akse parallel med den givne akse er jeg C , så ifølge denne sætning
jeg O = jeg C + Ml 2
hvor
M er hele kroppens masse
l er den vinkelrette afstand mellem to akser.
Inertimomenter for forskellige objekter
Inertimoment af forskellige objekter diskuteres nedenfor i denne artikel
Inertimoment af en rektangulær plade
Hvis pladens masse er M, længde l og bredde b, så passerer inertimomentet gennem tyngdepunktet og omkring en akse vinkelret på pladens plan.

I = M(l 2 + b 2 / 12)
Inertimoment af en skive
Hvis skiven har en masse M og radius r, så er inertimomentet omkring skivens geometriske akse

I = 1/2(Mr 2 )
Inertimoment af en stang
Hvis stangens masse er M og længden er l, så er inertimomentet om aksen vinkelret på stangens længde og passerer gennem dens tyngdepunkt

I = ML 2 /12
Inertimoment af en cirkel
Hvis ringens masse er M, og ringens radius er r, så er inertimomentet omkring aksen, der går igennem vinkelret på ringens centrum,

Jeg = Hr 2
Inertimoment af en sfære
Hvis en fast kugle har en masse på M og en radius på r, så er inertimomentet omkring dens diameter

I = 2/5Mr 2
Inertimoment af solid cylinder
Inertimomentet for en massiv cylinder med radius 'R' og masse M er givet af

I = 1/2MR 2
Inertimoment af hul cylinder
En hul cylinder har to radier, nemlig indre radius og ekstern radius. Inertimomentet for en hul cylinder med masse M, ydre radius R1, og indre radius R2er givet som

I = 1/2M(R 1 2 + R 2 2 )
Inertimoment af fast sfære
Inertimomentet for en solid massekugle 'M' og radius 'R' er angivet som

I = 2/5MR 2
Den hule kugles inertimoment
Inertimomentet for en hul kugle med masse M og radius 'R' er angivet som

I = 2/3MR 2
Ringens inertimoment
Inertimomentet for en ring er givet for to tilfælde, hvor rotationsaksen passerer gennem centrum, og når rotationsaksen passerer gennem diameteren.
Ringens inertimoment om aksen, der passerer gennem midten, er givet af
konverter streng til int

I = MR 2
Ringens inertimoment om aksen, der går gennem diameteren, er givet af

Jeg = Hr 2 /2
Squares inertimoment
Inertimomentet for kvadratet på side 'a' er givet som

I = a 4 /12
Inertimomentet for en firkantet plade på siden af længden 'l' og massen M er angivet som
I = 1/6ml 2
Trekantets inertimoment
Inertimomentet for en trekant er givet for 3 situationer, først når aksen passerer gennem midten, for det andet når aksen passerer gennem basen og for det tredje når aksen er vinkelret på basen. Lad os se formlen for dem én efter én. For en trekant med basis 'b' og højde 'h' er formlen for inertimoment givet som følger

Når aksen passerer gennem Centroid
I = bh 3 /36
Når aksen passerer gennem basen
I = bh 3 /12
Når aksen er vinkelret på basen
I = (hb/36)(b 2 – b 1 b + b 1 2 )
Forskellen mellem inertimoment og inerti
Forskellen mellem inerti og inertimoment er tabel nedenfor:
| Ja Nej. | Træghed | Inertimoment |
|---|---|---|
| 1. | Dens betydning er i lineær bevægelse. | Dens betydning er i rotationsbevægelse. |
| 2. | Det er den egenskab ved et objekt, der modsætter sig ændringen af objektets tilstand i lineær bevægelse. | Inertimomentet er den egenskab ved et objekt, som modsætter sig ændringen af objektets tilstand i rotationsbevægelse. |
| 3. | Et objekts inerti afhænger kun af dets masse. | Et objekts inertimoment afhænger af dets masse og dets massefordeling i forhold til rotationsaksen. |
| 4. | Et objekts inerti er fast. | Et objekts inertimoment varierer med hensyn til forskellige rotationsakser. |
Kinetisk energi af roterende krop
Lad os antage et legeme med masse 'm', der roterer med hastigheden v i en afstand 'r' fra rotationsaksen. Dens vinkelhastighed er så givet ved ω = v/r derefter v = rω. Nu ved vi, at Kinetisk energi af en krop er givet af
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2åh2
⇒ KE = 1/2Iω 2
Derfor er den kinetiske energi af et roterende legeme givet af halvdelen af produktet af inertimomentet og Vinkelhastighed af kroppen. Den kinetiske energi af roterende krop kaldes også Rotations kinetisk energi . Formlen for rotationskinetisk energi er givet som
KE = 1/2Iω 2
Inertimomentet(I) er uafhængigt af kroppens vinkelhastighed. Det er en funktion af massen af det roterende legeme og kroppens afstand fra rotationsaksen. Derfor observerer vi, at vinkelbevægelse er analog med lineær bevægelse, det betyder, at betydningen af inertiamoment er, at det giver en idé om, hvordan masser er fordelt i forskellige afstande fra rotationsaksen i et roterende legeme.
Anvendelse af inertimoment
Moment of Inertia har forskellige applikationer, hvoraf nogle er diskuteret nedenfor:
- På grund af det større inertimoment roterer jorden om sin akse med samme vinkelhastighed.
- Et lille bevægeligt hjul er placeret under børnenes legemotor. Efter at have gnidet dette hjul med jorden og forladt motoren, på grund af hjulets inertimoment, fortsætter motoren med at køre i nogen tid.
- Hver motor består af et stort og tungt hjul, der er fastgjort til sin aksel, med det meste af sin masse på sin omkreds. Derfor er dets inertimoment højt. Dette hjul kaldes et svinghjul. Drejningsmomentet, der driver motorens aksel, bliver ved med at stige. Derfor er rotationen af akslen muligvis ikke ensartet, men på grund af tilstedeværelsen af et bevægeligt hjul med mere inerti, fortsætter akslen med at rotere med en næsten ensartet hastighed.
- I hjulet af tyrevogne, rickshaws, scootere, cykler osv. er det meste af massen koncentreret på dens cirkel eller kant. denne bøjle eller rutine er fastgjort til hjulets akse med stive eger. Ved at gøre dette øges dets inertimoment. Derfor, når benene holder op med at bevæge sig under cykling, fortsætter hjulet med at snurre i nogen tid.
Tjek også
- Kinematik af rotationsbevægelse
- Bevægelse af en stiv krop
- Rullende bevægelse
Løste eksempler på inertimomenter
Eksempel 1: Et legeme med en masse på 500 g roterer om en akse. afstanden mellem kroppens massecenter og rotationsaksen er 1,2 m. find kroppens inertimoment om rotationsaksen.
Løsning:
Givet at M = 500 g = 0,5 kg, r = 1,2 m.
Det er klart, at hele massen af et legeme kan antages at være placeret i dets massecentrum. Derefter kroppens inertimoment om rotationsaksen.
Jeg = Hr2
I = 0,5 × (1,2)2
I = 0,72 kg m2
Eksempel 2: Omdrejningsradius om en akse 12 cm væk fra massecentret af et legeme med masse 1,2 kg er 13 cm. Beregn Omdrejningsradius og inertimoment om en akse, der går gennem massecentret.
Løsning:
Givet det, M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, ICM= ?
Fra sætning om parallelakse I = ICM+ Ml2
K2= KCM2+ l2
eller KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
KCM= 5
Nu, inertimoment ICM= MKCM2
jegCM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
Eksempel 3: Et legeme med en masse på 0,1 kg roterer om en akse. hvis afstanden mellem kroppens massecenter og rotationsaksen er 0,5 m, så find kroppens inertimoment.
Løsning:
Givet det, M = 0,1 kg og r = 0,5 m
så jeg = Hr2
I = 0,1 × (0,5)2
strengformatI = 0,025 kg m2
Eksempel 4: Ringenes inertimoment om en akse, der går gennem dens centrum vinkelret på den cirkulære ringplan er 200 gm cm 2 . Hvad vil inertimomentet være omkring dets diameter?
Løsning:
Inertimoment af en cirkulær ring omkring en akse, der går gennem et andet center vinkelret på dets plan
HR2= 200 gm cm2
Inertimoment ved at nå diameteren
= 1/2 MR2
= 1/2 × 200 = 100 gm cm2
Ofte stillede spørgsmål om Moments of Inertia
Hvordan beregner man inertimomentet?
Den grundlæggende formel for at finde inertimomentet for et ensartet objekt er,
jeg = hr 2
hvor,
m er massen af objektet'
r er afstanden fra rotationsaksen
Hvordan beregner man inertimomentet for en stråle?
Inertimoment for en bjælke langs midten og aksen vandret til den beregnes ved hjælp af formlen,
I = ML 2 / 12
Hvad afhænger et legemes inertimoment af?
Ethvert objekts inertimoment afhænger af de faktorer, der er angivet nedenfor:
- Kroppens masse,
- Rotationsakse
- Objektets form og størrelse
Hvad er enheden for inertimoment?
Enheden for Inertimoment er Kgm 2
Kan inertimomentet være negativt?
Nej, inertimomentet kan aldrig være negativt.
Hvad er masseinertimoment?
Masse-inertimoment er måling af en krops modstand mod ændringer i dets vinkelmomentum eller retning. Masseinertimomentet for en punktmasse er givet ved I = mr2og for system af partikler er masseinertimomentet givet som I = Σjegmjegrjeg2
Hvad er areal inertimoment?
Arealinertimoment er egenskab for et 2D-formplan, som viser, hvordan punkter er spredt i forhold til en vilkårlig akse i et plan. Arealinertimoment er også kendt som andet arealmoment eller kvadratisk arealmoment. Formlen for områdeinertimoment i xy-plan er givet som Ixy= ∫xy dxdxy = ∫xy dA
