Lignende udtryk er udtryk i algebraiske udtryk, der har de samme variable ophøjet til de samme potenser. Lige- og ulige-udtryk er typerne af udtryk i algebra, og vi kan skelne mellem lignende og ulige udtryk ved blot at kontrollere variablerne og deres magter. Vi definerer algebraiske termer som de individuelle termer opnået fra den algebraiske ligning.
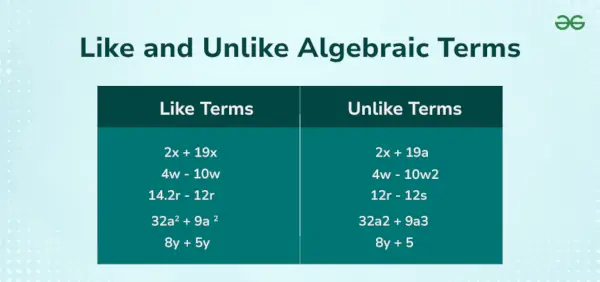
For eksempel i den algebraiske ligning 5x + 3 år 2 = 12 vi har tre udtryk, der er, 5x, 3y², og 12 . Her, 5x, og 3 år 2 er variable led, og 12 er konstantleddet. Billedet nedenfor viser lignende og ulige udtryk.
I denne artikel vil vi lære mere om vilkår for lignende, i modsætning til vilkår, deres eksempler, forenkling og andre i detaljer.
Synes godt om vilkår
Ens udtryk er de udtryk, der har de samme variabler, og styrken af hver af variablerne er også den samme. Vi kan kombinere lignende udtryk for at forenkle de algebraiske udtryk, og dette kan beregnes meget nemt. For eksempel er 3y + 5y et algebraisk udtryk med ens udtryk 3y og 5y. For at forenkle dette algebraiske udtryk tilføjer vi lignende udtryk. Således er forenklingen af det givne udtryk 8y.
Eksempler på lignende udtryk
Ligesom udtryk, er de udtryk, der har den samme variabel med lignende magt. Nogle eksempler på lignende udtryk er,
- 40xy 2 og 56xy 2 : I det første eksempel xy2er den fælles koefficient for begge led. Så de er ligesom udtryk.
- 30z 2 og 18z 2 : Med2er den fælles koefficient for begge led. Så de er ligesom udtryk.
- 45abc og 29abc: abc er den fælles koefficient for begge led. Så de er ligesom udtryk.
- 18r 3 og 38r 3 : r3er den fælles koefficient for begge led. Så de er ligesom udtryk.
- 2xy og 8xy: xy er den fælles koefficient for begge led. Så de er ligesom udtryk.
Tilføjelse og subtraktion af lignende vilkår
Vi kan nemt udføre addition og subtraktion af lignende udtryk, og det kræver ikke nogen speciel regel, de er generelt forenklet ved at bruge de normale additions- og subtraktionsregler. Vi kan forstå dette koncept ved at bruge følgende eksempel.
Eksempel: Forenkling 11x 3 + 5x 3
sortering array i java
Løsning:
Som vi ser, at disse er som udtryk, fordi de har lignende variabler, og deres styrke er også konstant.
Vi kan nemt tilføje disse udtryk direkte.
= 11x3+ 5x3
= 16x3
Dette er muligt, fordi de har de samme variabler med lignende styrke, og dette kan forstås som, at vi direkte kan tilføje rupees til rupees, dvs. 5 Rs + 7 Rs er 12 Rs. Men vi kan ikke direkte tilføje rupier med dollars, og 5 Rs + 7 Dollars kan ikke direkte forenkles.
På samme måde kan vi også trække lignende udtryk direkte, bare tilføje vi tilføjer lignende udtryk, dette kan forstås af følgende eksempel.
Eksempel 1: Forenkling 11x 3 – 5x 3
Løsning:
Som vi ser, at disse er som udtryk, fordi de har lignende variabler, og deres styrke er også konstant.
Vi kan nemt trække disse vilkår direkte fra.
= 11x3– 5x3
= 6x3
Eksempel 2: Tilføj 3 x + 2 og + 5 og 4 x - 3 og + 7.
java tilfældigt tal
Løsning:
(3 x + 2 og + 5) + (4 x - 3 og + 7)
= (3 x + 4x) +(2y + (-3y))+ (5 + 7)
= 7 x − og + 12
I modsætning til vilkår
I modsætning til termer er termer med forskellige variabler, og hver af variablerne kan have forskellige eksponenter på dem eller ikke. For eksempel er 9x + 6y et algebraisk udtryk med i modsætning til termer. Fordi den har to forskellige variable x og y.
Hvis variablerne er forskellige, kontrollerer vi ikke magten, da de på nogen måde er ulige termer, men hvis variablerne er de samme, kontrollerer vi for deres magter, fordi de kan være ens udtryk eller ikke.
Såsom 5x2og 6x2er ligesom udtryk, men 5x2og 6x3er ulige udtryk.
Eksempler på ulige vilkår
I modsætning til udtryk er de udtryk, der hverken har de samme variabler eller lignende magt. Nogle eksempler på ulige udtryk er,
få forbindelse
- 40xy 2 og 56xy: Her er variablen i et algebraisk udtryk xy2og i det andet algebraiske udtryk er variablen xy. Begge variabler er de samme, men har forskellige beføjelser. Så de er ulige udtryk.
- 45abc og 29ab: Her er variablen i det ene algebraiske udtryk abc og i det andet algebraiske udtryk er variablen ab. Begge variabler er forskellige. Så de falder ind under kategorien, i modsætning til termer.
Tilføjelse og subtraktion af ulige vilkår
Addition og subtraktion udføres ikke mellem, i modsætning til led, dvs. vi kan ikke tilføje eller trække ulige udtryk, og dette kan forstås af eksemplet, da vi ikke kan tilføje 5 liter mælk med 6 kg ris. På samme måde kan vi ikke tilføje eller trække fra, i modsætning til termer.
For eksempel kan 3xy + 5x ikke løses yderligere, og det efterlades på samme måde.
Forskellen mellem lignende vilkår og ulige vilkår
Forskellene mellem de lignende udtryk og i modsætning til udtryk diskuteres i tabellen nedenfor.
| Feature | Synes godt om vilkår | I modsætning til vilkår |
|---|---|---|
| Definition | Ens udtryk er de udtryk, der har de samme variabler og de samme eksponentværdier. | I modsætning til termer er udtryk, der har forskellige variabler og eksponenter. |
| Forenkling | Vi kan nemt forenkle lignende udtryk. | I modsætning til udtryk, der ikke kan forenkles. |
| Kombinere udtryk | Lignende udtryk kan kombineres direkte for at lave beregning. | I modsætning til termer kan ikke kombineres direkte, fordi de repræsenterer forskellige mængder |
| Addition eller subtraktion | Addition og subtraktion kan opnås på samme måde. | Vi kan ikke tilføje eller trække fra, i modsætning til termer. |
| Eksempler | Eksempler på lignende udtryk er x2, 5x2, -11/3x2, etc. | Eksempler på ulige udtryk er x2og 5x3, -11/3x osv. |
Læs mere
- Algebraiske udtryk
- Typer af algebraiske udtryk
Eksempler på Algebraiske udtryk for Like og Unlike
Eksempel 1: Identificer lignende og ulige udtryk fra: 3x, 5xy, 18x 2 og 5x 3 , 29xy, 50x 3
Løsning:
Synes godt om og i modsætning til vilkår fra de givne vilkår er,
Synes godt om vilkår: (5xy, 29xy) og (5x3, 50x3)
I modsætning til vilkår: 3x, 18x2og
Eksempel 2: Forenkle 3xy + 5x 2 + 11ab – 4xy
Løsning:
Givet udtryk: 3xy + 5x2+ 11ab – 4xy
Ligesom led i det givne udtryk, 3xy og -4xy
Om at forenkle,
= 3xy – 4xy + 5x2+ 11ab
delvis differentiering i latex= -xy + 5x2+ 11ab
Resten er alle vilkårene ulig vilkårene, så de kan ikke løses yderligere.
Eksempel 3: Forenkling 8x + 15x 2 + 11x – 4x 2
Løsning:
det dejligste smil i verden
Givet udtryk: 8x + 15x2+ 11x – 4x2
Ligesom led i det givne udtryk, (8x, 11x) og (15x2, -4x2)
Om at forenkle,
= 8x + 11x + 15x2– 4x2
= 19x – 11x2
Resten er alle vilkårene ulig vilkårene, så de kan ikke løses yderligere.
Kan lide og i modsætning til algebraiske vilkår – ofte stillede spørgsmål
Hvad er algebraiske udtryk?
Algebraiske termer er de individuelle termer opnået fra den algebraiske ligning, dvs. led divideret med operationssymboler såsom + og -.
Hvad er vilkårene for Like og Unlike?
Ligesom og ulige udtryk er udtryk for det algebraiske udtryk. I lignende har vi lignende variabler, og eksponentens magt er den samme, mens variablerne og deres magt i modsætning til hinanden er forskellige.
Hvad er forskellen mellem Algebraiske udtryk som ligner og ulige?
Den grundlæggende forskel mellem lignende og ulige udtryk er, at i det lignende udtryk har vi den samme variabel med de samme kræfter, mens vi i modsætning til udtryk har forskellige variabler med forskellige kræfter.
Hvordan finder man Algebraiske udtryk for Like og Unlike?
De lignende udtryk er de udtryk, der har de samme variabler med de samme beføjelser, og de ulige udtryk er udtryk med forskellige variabler og forskellige beføjelser, og vi kan nemt identificere dem blot ved at inspicere variablerne.
Kan vi tilføje eller trække lignende algebraiske udtryk?
Vi kan nemt tilføje eller trække lignende udtryk som 5x og 11x er lignende udtryk, og de kan tilføjes som 16x.
Kan vi tilføje eller trække i modsætning til algebraiske udtryk?
Vi kan ikke tilføje eller trække fra i modsætning til udtryk som 2x og 3y. I modsætning til termer kan således ikke lægges sammen eller trækkes fra.
