Den aritmetiske værdi, der bruges til at repræsentere mængden og bruges til at lave beregninger, er defineret som tal. Et symbol som 4, 5, 6, der repræsenterer et tal, er kendt som et tal. Uden tal kan vi ikke foretage optælling af ting, dato, tid, penge osv., disse tal bruges også til måling og bruges til mærkning.

Egenskaberne ved tal gør dem nyttige til at udføre aritmetiske operationer på dem. Disse tal kan skrives i numeriske former og også i ord.

For eksempel , 3 skrives som tre i ord, 35 skrives som femogtredive i ord osv. Elever kan skrive tallene fra 1 til 100 i ord for at lære mere.

Der er forskellige typer tal, som vi kan lære. De er hele og naturlige tal, ulige og lige tal, rationelle og irrationelle tal osv.

Hvad er et talsystem?

Et talsystem er en metode til at vise tal ved at skrive, som er en matematisk måde at repræsentere tallene i et givet sæt, ved at bruge tallene eller symbolerne på en matematisk måde. Skrivesystemet til at angive tal ved hjælp af cifre eller symboler på en logisk måde er defineret som talsystem.

Vi kan bruge cifrene fra 0 til 9 til at danne alle tallene. Med disse cifre kan enhver skabe uendelige tal.

For eksempel 156, 3907, 3456, 1298, 784859 osv.

Hvad er en kvadratrod?

Værdien af ​​et antal kvadratrødder, som ved multiplikation af sig selv giver det oprindelige tal. Antag, at a er kvadratroden af ​​b, så er den repræsenteret som a = √b, eller vi kan udtrykke den samme ligning som a2 = b. Her betegnes '√' dette symbol, vi brugte til at repræsentere roden af ​​tal, som radikalt. Det positive tal, når det skal ganges med sig selv, repræsenterer kvadratet på tallet. Kvadratroden af ​​kvadratet af ethvert positivt tal giver det oprindelige tal.

For eksempel, kvadratet af 4 er 16, 4²= 16, og kvadratroden af ​​16, √16 = 4. Da 4 er et perfekt kvadrat, er det derfor nemt at finde kvadratroden af ​​sådanne tal, men for et uperfekt kvadrat er det virkelig svært.

Kvadratrod er repræsenteret som '√' Det kaldes et radikalt symbol. For at repræsentere et tal 'a' som en kvadratrod ved hjælp af dette symbol kan det skrives som: '√a', hvor a er tallet.

r på c-sprog

Tallet her under det radikale symbol kaldes radicand. For eksempel er kvadratroden af ​​4 også repræsenteret som en radikal af 4. Begge repræsenterer den samme værdi.

Formlen til at finde kvadratroden er: a = √b

arraylist sortering

Egenskaber af kvadratrødder

Det er defineret som en en-til-en funktion, der tager et positivt tal som input og returnerer kvadratroden af ​​det givne inputtal.

f(x) = √x

For eksempel, hvis x = 9, returnerer funktionen outputværdien som 3.

Egenskaberne for kvadratroden er som følger:

• Hvis et tal er et perfekt kvadrattal, så eksisterer der helt sikkert en perfekt kvadratrod.
• Hvis et tal ender med et lige tal af nuller (0'er), så kan vi have en kvadratrod.
• De to kvadratrodsværdier kan ganges. For eksempel kan √3 ganges med √2, så bliver resultatet √6.
• Når to ens kvadratrødder ganges, så skal resultatet være et radikalt tal. Det viser, at resultatet er et ikke-kvadratrodstal. For eksempel, når √7 ganges med √7, er det opnåede resultat 7.
• Kvadratroden af ​​negative tal er udefineret. Derfor kan det perfekte kvadrat ikke være negativt.
• Nogle af tallene slutter med 2, 3, 7 eller 8 (i enhedscifferet), så eksisterer den perfekte kvadratrod ikke.
• Nogle af tallene slutter med 1, 4, 5, 6 eller 9 i enhedscifferet, så vil tallet have en kvadratrod.

Det er nemt at finde kvadratroden af ​​et tal, der er et perfekt kvadrat.

Perfekte firkanter er de positive tal, der kan skrives som multiplikationen af ​​et tal med sig selv, eller man kan sige, at et perfekt kvadrat er et tal, der er værdien af ​​potens 2 af ethvert heltal.

Det tal, der kan udtrykkes som produktet af to lige store heltal. For eksempel er 16 et perfekt kvadrat, fordi det er produktet af to lige store heltal, 4 × 4 = 16. 24 er dog ikke et perfekt kvadrat, fordi det ikke kan udtrykkes som produktet af to lige store heltal. (8 x 3 = 24).

Tallet, der opnås ved at kvadrere et helt tal, betegnes som et perfekt kvadrat.

Hvis vi antager, at N er et perfekt kvadrat af et helt tal y, kan dette skrives som N = produktet af y og y = y².

Så den perfekte kvadratiske formel kan udtrykkes som:

N = Y ²

Lad os bruge formlen med værdier:

Hvis y = 9, og N = y²

Det betyder, N = 9²= 81.

Her er 81 et perfekt kvadrat på 9, fordi det er kvadratet af et helt tal.

Ved hjælp af kvadratrødder kan vi identificere, om et tal er et perfekt kvadrat eller ej, hvis vi beregner kvadratroden af ​​det givne tal.

Hvis kvadratroden er et helt tal, vil det givne tal være et perfekt kvadrat, og hvis kvadratrodsværdien ikke er et helt tal, så er det givne tal ikke et perfekt kvadrat.

prioritetskø c++

For eksempel, for at kontrollere, om 24 er et perfekt kvadrat eller ej, beregner vi dens kvadratrod. √24 = 4,898979. Som vi kan se, er 4,898979 ikke et helt tal, så 24 er ikke et perfekt kvadrat.

Lad os tage et andet eksempel på

inorder gennemkøring

Tallet 49. √49 = 7. Vi kan se, at 7 er et helt tal, derfor er 49 et perfekt kvadrat.

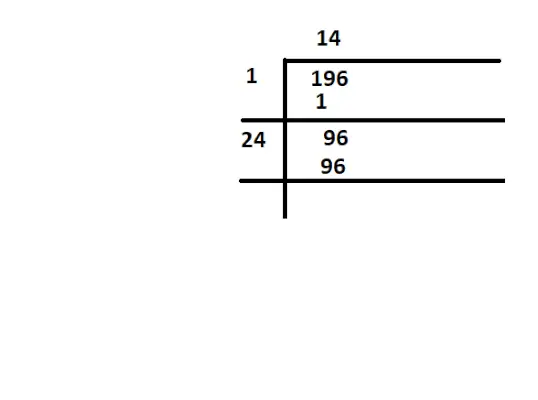
Er 196 en perfekt plads?

Løsning:

For at kontrollere, om 196 er et perfekt kvadrat, skal vi finde kvadratrødderne af 196

perfekt kvadrat på 196

Her er kvadratroden af ​​196 14

Perfekte kvadrater er de positive tal, der kan skrives som multiplikationen af ​​et tal med sig selv, eller du kan sige, at et perfekt kvadrat er et tal, der er værdien af ​​potens 2 af ethvert heltal.

Her kan vi skrive √196 = 14 eller 14²= 14 × 14 = 196.

Derfor er 196 et perfekt kvadrat.

Lignende spørgsmål

Spørgsmål 1: Hvad er kvadratroden af ​​625?

Løsning:

perfekt kvadrat på 625

database design i dbms

her er 625 perfekt kvadrat på 25

Så vi kan skrive som √625 = 25 eller 25²= 25 × 25 = 625

Spørgsmål 2: Hvordan finder du kvadratroden af ​​24?

Løsning:

kvadratroden af ​​24

Her er 24 ikke et perfekt kvadrat på 4,8989..

Derfor √24 = 4,8989..

Spørgsmål 3: Find kvadratroden af ​​361?

Løsning:

kvadrat på 361

Her er kvadratroden af ​​361 19 , et helt tal, som er et perfekt kvadrat

Derfor √361 = 19 eller 19²= 19 × 19 = 361