EN Instrueret acyklisk graf , ofte forkortet som DAG , er et grundlæggende begreb i grafteori. DAG'er bruges til at vise, hvordan tingene hænger sammen eller afhænger af hinanden på en klar og organiseret måde. I denne artikel skal vi lære om Instrueret acyklisk graf , dets egenskaber og anvendelse i det virkelige liv.

Instrueret acyklisk graf
Hvad er rettet acyklisk graf?
EN Instrueret acyklisk graf (DAG) er en rettet graf, der ikke indeholder nogen cyklusser.
Nedenstående graf repræsenterer en rettet acyklisk graf (DAG):

Direkte acyklisk graf
Betydning af rettet acyklisk graf:
Instrueret acyklisk graf har to vigtige funktioner:
- Instrueret Edge s:I instrueret acyklisk graf, hver kant har en retning, hvilket betyder, at den går fra et toppunkt (knudepunkt) til et andet. Denne retning betyder en en vej forhold eller afhængighed mellem noder.
- Acyklisk: Begrebet acyklisk angiver, at der ikke er nogen cyklusser eller lukkede sløjfer i grafen. Med andre ord, du kan ikke krydse en sekvens af rettede kanter og vende tilbage til den samme knude og følge kantretningerne. Dannelse af cyklusser er forbudt i DAG. Derfor er denne egenskab væsentlig.

Instrueret acyklisk graf
Egenskaber for Directed Acyclic Graph DAG:
Directed Acyclic Graph (DAG) har forskellige egenskaber, der gør dem anvendelige i grafproblemer.
Der er følgende egenskaber ved Directed Acyclic Graph (DAG):
- Relation til tilgængelighed: I DAG kan vi bestemme, om der er en tilgængelighedsrelation mellem to noder. Node A siges at være tilgængelig fra node B, hvis der findes en rettet sti, der starter ved node B og slutter ved node A. Dette indebærer, at du kan følge retningen af kanter i grafen for at komme fra B til A.
- Transitiv lukning: Den transitive lukning af en rettet graf er en ny graf, der repræsenterer alle de direkte og indirekte relationer eller forbindelser mellem noder i den originale graf. Med andre ord fortæller den dig, hvilke noder der kan nås fra andre noder ved at følge en eller flere rettede kanter.
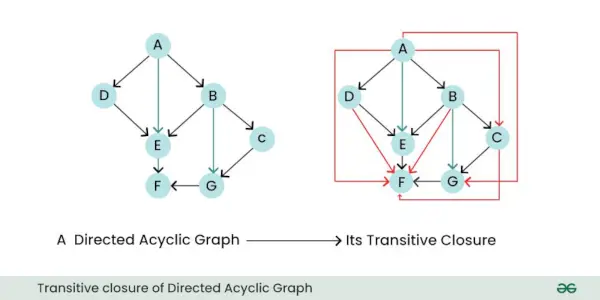
Transitiv lukning af rettet acyklisk graf
- Transitiv reduktion: Den transitive reduktion af en rettet graf er en ny graf, der kun bevarer de væsentlige, direkte relationer mellem noder, samtidig med at alle unødvendige indirekte kanter fjernes. I bund og grund forenkler det grafen ved at eliminere kanter, der kan udledes af de resterende kanter.
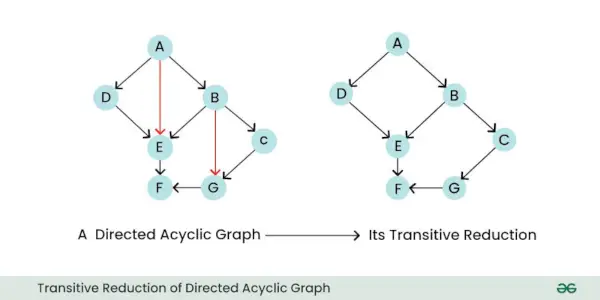
Transitiv reduktion af rettet acyklisk graf
- Topologisk rækkefølge: En DAG kan sorteres topologisk, hvilket betyder, at du lineært kan ordne dens noder på en sådan måde, at for alle kanterne, startknudepunktet for kanten forekommer tidligere i sekvensen. Denne egenskab er nyttig til opgaver som planlægning og afhængighedsløsning.
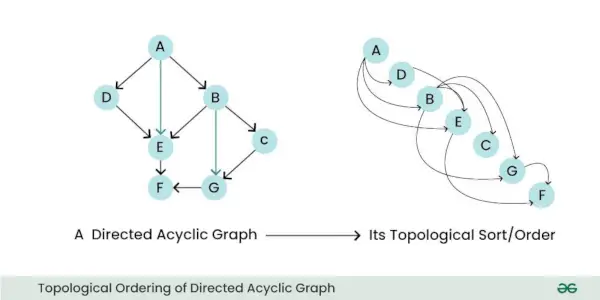
Topologisk rækkefølge af rettet acyklisk graf
Praktiske anvendelser af DAG:
- Analyse af dataflow: I compilerdesign og optimering bruges DAG'er til at repræsentere dataflow i et program. Dette hjælper med at optimere kode ved at identificere redundante beregninger og død kode. DAG'er bruges også til at repræsentere strukturen af grundblokke i Compiler Design.
- Opgaveplanlægning: DAG'er bruges i projektledelse og jobplanlægning. Hver opgave eller job er repræsenteret som en node i DAG'en med rettede kanter, der angiver afhængigheder. Den acykliske karakter af DAG sikrer, at opgaver er planlagt i en logisk rækkefølge, hvilket forhindrer cirkulære afhængigheder.
En vægtet rettet acyklisk graf kan bruges til at repræsentere et planlægningsproblem. Lad os tage eksemplet med et opgaveplanlægningsproblem. Her kan et toppunkt repræsentere opgaven, og dets vægt kan repræsentere størrelsen af opgaveberegningen. På samme måde kan en kant repræsentere kommunikationen mellem to opgaver, og dens vægt kan repræsentere omkostningerne ved kommunikation:
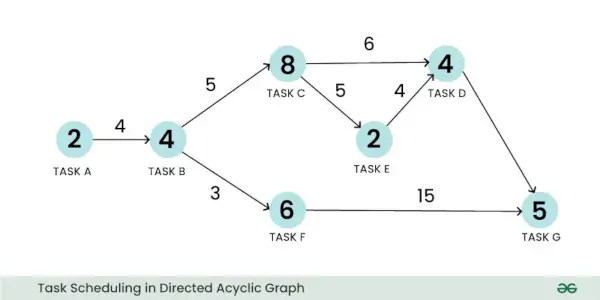
Opgaveplanlægning i rettet acyklisk graf
Konklusion:
Sammenfattende er Directed Acyclic Graphs et grundlæggende begreb inden for grafteori med adskillige praktiske anvendelser. DAG'er spiller en afgørende rolle i opgaveplanlægning, dataflowanalyse, afhængighedsløsning og forskellige andre områder inden for datalogi og teknik. De hjælper med at optimere processer, styre afhængigheder og sikre effektiv udførelse af opgaver eller job.
