Binært søgetræ er en datastruktur, der bruges i datalogi til at organisere og lagre data på en sorteret måde. Binært søgetræ følger alle egenskaber for binært træ og dets venstre child indeholder værdier mindre end den overordnede node og højre barn indeholder værdier, der er større end den overordnede node. Denne hierarkiske struktur giver mulighed for effektiv Søger , Indskud , og Sletning operationer på de data, der er gemt i træet.
Binært søgetræ
en million i tal
Indholdsfortegnelse
- Hvad er binært søgetræ?
- Egenskaber for binært søgetræ
- Håndtering af duplikerede værdier i det binære søgetræ
- Operationer udført på en BST
- 1. Søgning efter en node i BST
- 2. Indsæt en node i en BST
- 3. Slet en node af BST
- 4. Traversal (Inorder traversal af BST)
- Anvendelser af BST
- Fordele
- Ulemper
- FAQ (ofte stillede spørgsmål) om binært søgetræ:
Hvad er binært søgetræ?
Binært søgetræ (BST) er en speciel type binært træ hvor det venstre underordnede af en knude har en værdi, der er mindre end knudepunktets værdi, og det højre underordnede har en værdi, der er større end knudepunktets værdi. Denne egenskab kaldes BST-egenskaben, og den gør det muligt effektivt at søge, indsætte og slette elementer i træet.
Egenskaber for binært søgetræ:
- Det venstre undertræ af en node indeholder kun noder med nøgler, der er mindre end nodens nøgle.
- Det højre undertræ af en node indeholder kun noder med nøgler, der er større end nodens nøgle.
- Det betyder, at alt til venstre for roden er mindre end værdien af roden, og alt til højre for roden er større end værdien af roden. På grund af denne ydeevne er en binær søgning meget let.
- Det venstre og højre undertræ skal hver også være et binært søgetræ.
- Der må ikke være nogen duplikerede noder (BST kan have duplikerede værdier med forskellige håndteringsmetoder)
Håndtering af duplikerede værdier i det binære søgetræ:
- Vi skal følge en konsistent proces hele vejen igennem, dvs. enten gemme duplikatværdien til venstre eller gemme duplikatværdien til højre for roden, men være konsekvent med din tilgang.
Grundlæggende handlinger på binært søgetræ:
1. Søgning efter en node i BST:
At søge i BST betyder at lokalisere en specifik node i datastrukturen. I binært søgetræ er det let at søge i en node på grund af dens en specifik rækkefølge. Trinnene til at søge en node i binært søgetræ er angivet som følger -
- Sammenlign først det element, der skal søges i, med træets rodelement.
- Hvis root matches med målelementet, returner derefter nodens placering.
- Hvis det ikke er matchet, så tjek om elementet er mindre end rodelementet, hvis det er mindre end rodelementet, så flyt til venstre undertræ.
- Hvis det er større end rodelementet, så flyt til højre undertræ.
- Gentag ovenstående procedure rekursivt, indtil matchen er fundet.
- Hvis elementet ikke findes eller ikke findes i træet, returneres NULL.
Lad os nu forstå søgningen i binært træ ved hjælp af et eksempel:
Nedenfor er givet en BST, og vi skal søge efter element 6.
Kode:
Nedenfor er implementeringen af søgning i BST:
onclick javascriptC++
// C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // En hjælpefunktion til at indsætte // en ny node med givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL ) returner nyNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) node->venstre = indsæt(node->venstre, nøgle); else if (nøgle> node->nøgle) node->højre = indsæt(node->højre, nøgle); // Returner (uændret) node pointer return node; } // Hjælpefunktion til at søge efter en nøgle i en BST struct node* search(struct node* root, int key) root->key == key) return root; // Nøglen er større end roots nøgle if (root->key< key) return search(root->højre, nøgle); // Nøglen er mindre end roots nøgleretursøgning(root->venstre, nøgle);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // En hjælpefunktion til at indsætte // en ny node med givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL ) returner nyNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) node->venstre = indsæt(node->venstre, nøgle); else if (nøgle> node->nøgle) node->højre = indsæt(node->højre, nøgle); // Returner (uændret) node pointer return node; } // Hjælpefunktion til at søge efter en nøgle i en BST struct node* søgning(struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>node.key) node.right = insert(node.right, key); // Returner (uændret) node pointer return node; } // Hjælpefunktion til at søge efter en nøgle i en BST-nodesøgning(Node-rod, int-nøgle) // Grundtilfælde: root er null eller nøgle er til stede ved root, hvis (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Returner (uændret) node pointer return node # Utility funktion til at søge efter en nøgle i en BST def search(root, key): # Basistilfælde: root er null eller nøgle er til stede ved root, hvis root er Ingen eller root.key == nøgle: returner root # Key er større end roots nøgle hvis root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner (uændret) node pointer return node; } // Hjælpefunktion til at søge efter en nøgle i en BST-funktionssøgning(root, key) { // Grundtilfælde: root er null eller nøgle er til stede ved root if (root === null || root.key === nøgle ) { returner rod; } // Nøglen er større end roots nøgle if (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Indsæt en node i en BST :
En ny nøgle er altid indsat ved bladet. Begynd at søge efter en nøgle fra roden til en bladknude. Når en bladknude er fundet, tilføjes den nye knude som et underordnet bladknudepunkt.
Kode:
Nedenfor er implementeringen af indsættelsen af en enkelt node i binært søgetræ:
linux $homeC++
// Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // Funktion til at indsætte en ny node med // givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL) returner newNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) { node->venstre = indsæt(node->venstre, nøgle); } else if (tast> node->key) { node->right = insert(node->right, key); } // Returner node pointer return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // Funktion til at indsætte en ny node med // givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL) returner newNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) { node->venstre = indsæt(node->venstre, nøgle); } else if (tast> node->key) { node->right = insert(node->right, key); } // Returner node pointer return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner noden returknude; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Returner nodemarkøren returknude>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner node pointer return node; }> Tidskompleksitet: O(N), hvor N er antallet af knudepunkter for BST
Hjælpeplads: O(1)
3. Slet en node af BST :
Den bruges til at slette en node med specifik nøgle fra BST'en og returnere den nye BST.
Forskellige scenarier for sletning af noden:
Node, der skal slettes, er bladknuden :
Det er enkelt, du kan bare fjerne det.
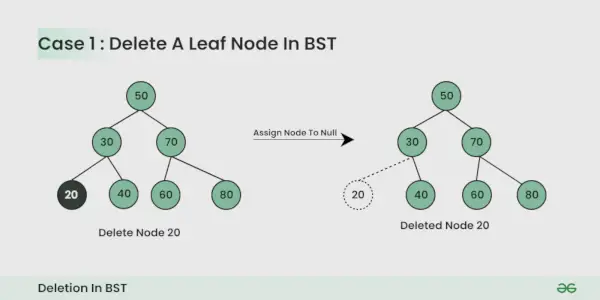
Node, der skal slettes, har et barn :
Du kan bare erstatte noden med den underordnede node.
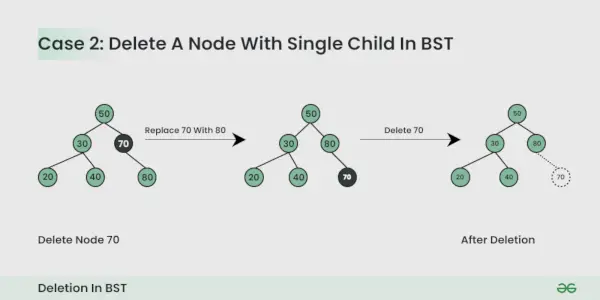
Node, der skal slettes, har to underordnede :
Her skal vi slet noden er sådan, at det resulterende træ følger egenskaberne for en BST. Tricket er at finde nodens efterfølger i uorden. Kopier indholdet af inorder-efterfølgeren til noden, og slet inorder-efterfølgeren.
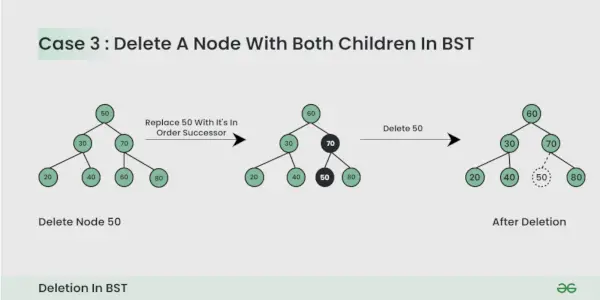
Pas på følgende ting, mens du sletter en node af en BST:
- Skal finde ud af, hvad der skal erstatte den node, der skal slettes.
- Ønsker minimal forstyrrelse af den eksisterende træstruktur
- Kan tage erstatningsknuden fra de slettede noder til venstre eller højre undertræ.
- Hvis vi tager if fra venstre undertræ, skal vi tage den største værdi i venstre undertræ.
- Hvis vi tager hvis fra det højre undertræ, skal vi tage den mindste værdi i det højre undertræ.
Kode:
Nedenfor er implementeringen af sletningen i BST:
kali linux terminalC++
// C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // Funktion til at indsætte en ny node med // givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL) returner newNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) { node->venstre = indsæt(node->venstre, nøgle); } else if (tast> node->key) { node->right = insert(node->right, key); } // Returner node pointer return node; } // Funktion, der returnerer noden med minimum // nøgleværdi fundet i det træ struct node* minValueNode(struct node* node) { struct node* current = node; // Loop ned for at finde bladet længst til venstre, mens (aktuel && strøm->venstre != NULL) strøm = strøm->venstre; returstrøm; } // Funktion der sletter nøglen og // returnerer den nye root struct node* deleteNode(struct node* root, int key) { // base Case if (root == NULL) returner root; // Hvis nøglen, der skal slettes, er // mindre end rodens nøgle, // så ligger den i venstre undertræ if (nøgle< root->key) { root->left = deleteNode(rod->venstre, nøgle); } // Hvis nøglen, der skal slettes, er // større end rodens nøgle, // så ligger den i højre undertræ ellers hvis (nøgle> root->nøgle) { root->right = deleteNode(root-> højre, nøgle); } // Hvis nøglen er den samme som root's nøgle, // så er dette noden // der skal slettes ellers { // Node med kun et barn // eller ingen underordnet hvis (root->venstre == NULL) { struct node* temp = root->right; fri(rod); retur temp; } else if (rod->højre == NULL) { struct node* temp = root->venstre; fri(rod); retur temp; } // Node med to børn: // Hent inorder successor(mindste // i højre undertræ) struct node* temp = minValueNode(root->right); // Kopier efterfølgerens // indhold til denne node root->key = temp->key; // Delete the inorder successor root->right = deleteNode(root->right, temp->key); } returnere rod; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // Funktion til at indsætte en ny node med // givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL) returner newNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) { node->venstre = indsæt(node->venstre, nøgle); } else if (tast> node->key) { node->right = insert(node->right, key); } // Returner node pointer return node; } // Funktion, der returnerer noden med minimum // nøgleværdi fundet i det træ struct node* minValueNode(struct node* node) { struct node* current = node; // Loop ned for at finde bladet længst til venstre, mens (aktuel && strøm->venstre != NULL) strøm = strøm->venstre; returstrøm; } // Funktion der sletter nøglen og // returnerer den nye root struct node* deleteNode(struct node* root, int key) { // base Case if (root == NULL) returner root; // Hvis nøglen, der skal slettes, er // mindre end rodens nøgle, // så ligger den i venstre undertræ if (nøgle< root->key) { root->left = deleteNode(rod->venstre, nøgle); } // Hvis nøglen, der skal slettes, er // større end rodens nøgle, // så ligger den i højre undertræ ellers hvis (nøgle> root->nøgle) { root->right = deleteNode(root-> højre, nøgle); } // Hvis nøglen er den samme som root's nøgle, // så er dette noden // der skal slettes ellers { // Node med kun et barn // eller ingen underordnet hvis (root->venstre == NULL) { struct node* temp = root->right; fri(rod); retur temp; } else if (rod->højre == NULL) { struct node* temp = root->venstre; fri(rod); retur temp; } // Node med to børn: // Hent inorder successor(mindste // i højre undertræ) struct node* temp = minValueNode(root->right); // Kopier efterfølgerens // indhold til denne node root->key = temp->key; // Delete the inorder successor root->right = deleteNode(root->right, temp->key); } returnere rod; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner noden returknude; } // Funktion, der returnerer noden med minimum // nøgleværdi fundet i træet statisk node minValueNode(node node) { node current = node; // Loop ned for at finde bladet længst til venstre, mens (current != null && current.left != null) current = current.left; returstrøm; } // Funktion der sletter nøglen og // returnerer den nye statiske rodnode deleteNode(node rod, int nøgle) { // base Case if (root == null) returner rod; // Hvis nøglen, der skal slettes, er // mindre end rodens nøgle, // så ligger den i venstre undertræ if (nøgle< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, nøgle); } // Hvis nøglen er den samme som root's nøgle, // så er dette noden // der skal slettes ellers { // Node med kun ét barn // eller intet barn if (root.left == null) { node temp = root.right; retur temp; } else if (root.right == null) { node temp = root.left; retur temp; } // Node med to børn: // Hent inorder successor(mindste // i højre undertræ) node temp = minValueNode(root.right); // Kopiér efterfølgerens // indhold til denne node root.key = temp.key; // Delete the inorder successor root.right = deleteNode(root.right, temp.key); } returnere rod; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Returner nodepointeren returner root # Funktion til at udføre en rækkefølgegennemgang af BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Funktion, der returnerer noden med minimum # nøgleværdi fundet i det træ def minValueNode(node): current = node # Loop ned for at finde bladet længst til venstre, mens nuværende og aktuel.venstre er ikke Ingen: aktuel = aktuel.venstre returner aktuel # Funktion, der sletter nøglen og # returnerer den nye rod def deleteNode(rod, nøgle): # base Sag hvis rod er Ingen: returner rod # Hvis nøglen skal være slettet er # mindre end rodens nøgle, # så ligger den i venstre undertræ hvis nøglen< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Hvis nøglen er den samme som roots nøgle, # så er dette noden #, der skal slettes ellers: # Node med kun ét barn # eller intet barn hvis root.left er Ingen: temp = root.right root = Ingen returner temp elif root.right er Ingen: temp = root.left root = Ingen retur temp # Node med to børn: # Hent efterfølgeren i uorden (mindste # i højre undertræ) temp = minValueNode(root.right) # Kopier efterfølgerens # indhold til denne node root.key = temp.key # Slet efterfølgeren root.right = deleteNode(root.right, temp.key) returner root>
4. Traversal (Inorder traversal af BST) :
I tilfælde af binære søgetræer (BST), giver Inorder traversal noder i ikke-faldende rækkefølge. Vi besøger først det venstre barn, så roden og så det højre barn.
Nedenfor er implementeringen af, hvordan man laver en rækkefølgegennemgang af et binært søgetræ:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // Funktion til at indsætte en ny node med // givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL) returner newNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) { node->venstre = indsæt(node->venstre, nøgle); } else if (tast> node->key) { node->right = insert(node->right, key); } // Returner node pointer return node; } // Funktion til at udføre inorder-gennemgang af BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); cout<< ' ' << root->nøgle; inorder(rod->højre); } } // Driverkode int main() { /* Lad os oprette følgende BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Oprettelse af BST-roden = insert(root, 50); indsæt(rod, 30); indsæt(rod, 20); indsæt(rod, 40); indsæt(rod, 70); indsætte(rod, 60); indsæt(rod, 80); // Funktion Kald inorder(root); retur 0; } // Denne kode er bidraget af shivanisinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->nøgle = vare; temp->venstre = temp->højre = NULL; retur temp; } // Funktion til at indsætte en ny node med // givet nøgle i BST struct node* insert(struct node* node, int key) { // Hvis træet er tomt, returner en ny node if (node == NULL) returner newNode(nøgle); // Ellers går du igen ned i træet, hvis (tast< node->key) { node->venstre = indsæt(node->venstre, nøgle); } else if (tast> node->key) { node->right = insert(node->right, key); } // Returner node pointer return node; } // Funktion til at udføre inorder-gennemgang af BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', root->nøgle); inorder(rod->højre); } } // Driverkode int main() { /* Lad os oprette følgende BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Oprettelse af BST-roden = insert(root, 50); indsæt(rod, 30); indsæt(rod, 20); indsæt(rod, 40); indsæt(rod, 70); indsætte(rod, 60); indsæt(rod, 80); // Funktion Kald inorder(root); retur 0; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Returner noden returknude; } // Funktion til at udføre inorder-gennemgang af BST static void inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); inorder(root.right); } } // Driverkode public static void main(String[] args) { /* Lad os oprette følgende BST 50 / 30 70 / / 20 40 60 80 */ node root = null; // indsætter værdi 50 root = indsæt(rod, 50); // indsættelse af værdi 30 insert(root, 30); // indsættelse af værdi 20 insert(rod, 20); // indsættelse af værdi 40 insert(root, 40); // indsættelse af værdi 70 insert(root, 70); // indsættelse af værdi 60 insert(root, 60); // indsættelse af værdi 80 insert(root, 80); // udskriv BST inorder(root); } } // Denne kode er bidraget af abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Returner nodepointeren returknude # Funktion til at udføre en rækkefølgegennemgang af BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Driverkode hvis __navn__ == '__main__': # Lad os oprette følgende BST # 50 # / # 30 70 # / / # 20 40 60 80 root = Ingen # Oprettelse af BST-roden = insert(rod, 50) insert(rod, 30) insert(rod, 20) insert(rod, 40) insert(rod, 70) insert(rod, 60) indsæt(rod, 60) , 80) # Funktion Kald inorder(root) #Denne kode er bidraget af japmeet01>
Produktion
20 30 40 50 60 70 80>
Tidskompleksitet: O(N), hvor N er antallet af knudepunkter for BST
Hjælpeplads: O(1)
Anvendelser af BST:
- Grafalgoritmer: BST'er kan bruges til at implementere grafalgoritmer, såsom i minimumspændende træalgoritmer.
- Prioriterede køer: BST'er kan bruges til at implementere prioritetskøer, hvor elementet med den højeste prioritet er ved roden af træet, og elementer med lavere prioritet gemmes i undertræerne.
- Selvbalancerende binært søgetræ: BST'er kan bruges som en selvbalancerende datastruktur, såsom AVL-træ og rød-sort træ.
- Datalagring og hentning: BST'er kan bruges til at gemme og hente data hurtigt, såsom i databaser, hvor søgning efter en specifik post kan udføres i logaritmisk tid.
Fordele:
- Hurtig søgning: Søgning efter en specifik værdi i en BST har en gennemsnitlig tidskompleksitet på O(log n), hvor n er antallet af noder i træet. Dette er meget hurtigere end at søge efter et element i et array eller linket liste, som i værste fald har en tidskompleksitet på O(n).
- Gennemgang i rækkefølge: BST'er kan krydses i rækkefølge, som besøger det venstre undertræ, roden og det højre undertræ. Dette kan bruges til at sortere et datasæt.
- Pladseffektiv: BST'er er pladseffektive, da de ikke gemmer nogen overflødig information, i modsætning til arrays og sammenkædede lister.
Ulemper:
- Skæve træer: Hvis et træ bliver skævt, vil tidskompleksiteten af søge-, indsættelses- og sletningsoperationer være O(n) i stedet for O(log n), hvilket kan gøre træet ineffektivt.
- Yderligere tid påkrævet: Selvbalancerende træer kræver yderligere tid til at opretholde balancen under indsættelses- og sletningsoperationer.
- Effektivitet: BST'er er ikke effektive til datasæt med mange dubletter, da de vil spilde plads.
FAQ'er(Ofte stillede spørgsmål)på binært søgetræ:
1. Hvad er et binært søgetræ?
Et binært søgetræ (BST) er et binært træ, hvor hver knude i det venstre undertræ er mindre end roden, og hver knude i det højre undertræ har en værdi større end roden . Egenskaberne for et binært søgetræ er rekursive: Hvis vi betragter en knude som en rod, vil disse egenskaber forblive sande.
2. Hvad er den binære søgetræoperation?
Der er tre store operationer i Binary Search Tree: 1. Indsættelse, 2. Sletning, 3. Søgning. På grund af dets egenskaber er det effektivt at søge efter ethvert element i Binary Search Tree.
3. Hvad er binært søgetræ og AVL-træ?
Binært søgetræ : Et binært søgetræ (BST) er et binært træ, hvor hver knude i det venstre undertræ er mindre end roden, og hver knude i det højre undertræ har en værdi, der er større end roden.
AVL træ : Binære søgetræer (BST'er), der selvbalancerer og roterer automatisk, er kendt som AVL-træer.
4. Hvad er brugen af Binary Search Tree?
Binære søgetræer kan bruges til at implementere abstrakte datatyper som f.eks dynamiske sæt, opslagstabeller og prioritetskøer, og bruges i sorteringsalgoritmer såsom træsortering.
5. Hvad er forskellen mellem binært søgetræ og binært træ?
Et binært søgetræ er et træ, der følger en eller anden rækkefølge for at arrangere elementerne, hvorimod det binære træ ikke følger nogen rækkefølge.
matrix multiplikation i c
Relaterede artikler:
- Anvendelse af BST
- Anvendelser, fordele og ulemper ved binært søgetræ
- Indsættelse i binært søgetræ (BST)
- Søgning i binært søgetræ (BST)
- Sletning i binært søgetræ (BST)
