Midten af ​​en trekant er skæringspunktet for alle tre vinkelhalveringslinjer i en trekant. Incentret er et vigtigt punkt i en trekant, hvor linjer, der skærer vinkler på midten, mødes. Dette punkt er også midten af ​​en cirkel kaldet Incircle, der passer perfekt inde i trekanten og rører alle tre sider ens. Denne artikel dækker forskellige begreber om trekantens midte, såsom hvorfor dette punkt er vigtigt, hvordan man finder det ved hjælp af et kompas eller tal og egenskaber for cirklens centrum.

Indholdsfortegnelse

• Hvad er midten af ​​en trekant?
• Egenskaber for et incenter af en trekant
• Formel i midten af ​​en trekant
• Sådan finder du midten af ​​en trekant
• Centroid, Circumcenter, Incenter, Orthocenter

Hvad er midten af ​​en trekant?

Midten af ​​en trekant er, som navnet antyder, trekantens midtpunkt. Dette punkt, som vi kalder et incenter, dannes i det kryds, hvor alle de linjer, der deler de indre vinkler, mødes. Punktets afstand fra alle tre sider af trekanten er den samme. Trekantens incirkel passer også til en perfekt cirkel inde i trekanten, og denne cirkel kaldes trekantens incirkel.

Incenter definition

Midten af ​​en trekant er det punkt inde i trekanten, hvor alle tre linjer, der skærer dens indvendige vinkler i to, mødes. Dette punkt er i samme afstand fra trekantens tre sider, hvilket gør det som trekantens midte. Det er også midten af ​​den største cirkel, der kan passe tæt ind i trekanten, som vi kalder incirkelen. For at symbolisere incenteret bruger vi typisk bogstavet I,

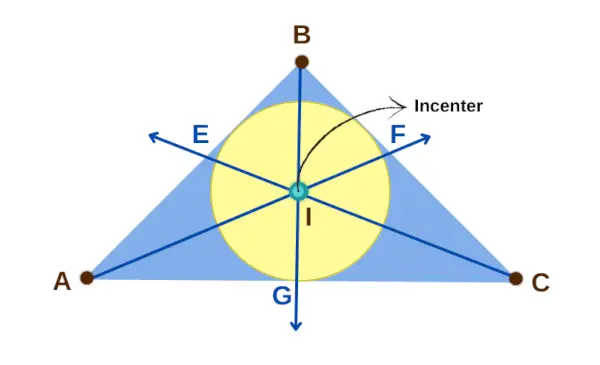
Midten af ​​en trekant

Egenskaber for et incenter af en trekant

Nogle vigtige egenskaber ved trekantens midte er givet nedenfor:

Ejendom 1: Hvis jeg er midten af ​​en trekant ABC, så er tre par linjestykker lige lange: AE og AG, CG og CF, og BF og BE. Det betyder, at AE = AG, CG = CF og BF = BE.

Ejendom 2: Incentret jeg har også et særligt forhold til trekantens vinkler. Det får vinklerne ∠BAI og ∠CAI til at være ens, ∠BCI og ∠ACI til at være ens, og ∠ABI og ∠CBI til at være ens. Dette følger vinkelhalveringspunktet.

Ejendom 3: Incentret jeg er midten af ​​en cirkel, der rører alle tre sider af trekanten, og afstandene fra jeg til siderne af trekanten (EI, FI, GI) er alle ens. Disse afstande kaldes inradii, eller radius af incirkelen.

Ejendom 4: Du kan beregne arealet af trekanten ved hjælp af semiperimeteren (s) og inradiusen (r). Formlen er A = sr, hvor A er arealet, s er halvperimeteren (s = (a + b + c)/2, hvor a, b og c er trekantens sidelængder), og r er trekanten inradius.

Ejendom 5: Midten af ​​en trekant forbliver altid inde i trekanten. I modsætning til ortocentret, som i nogle tilfælde kan være uden for trekanten, er incentret altid indeholdt inden for trekantens grænser.

Formel i midten af ​​en trekant

Formlen til at finde midten af ​​formlen med 3 koordinater (x₁, og₁), (x₂, og₂), og (x₃, og₃) er:

{(økse ₁ + bx ₂ + cx ₃ )/(a + b + c), (er ₁ + af ₂ + c ₃ )/(a + b + c)}

rekha filmskuespillerinde

Kort sagt, for at få centrum, skal du:

• Multiplicer x-koordinaten for punkt A med sidelængden a, x-koordinaten for punkt B med sidelængden b og x-koordinaten for punkt C med sidelængden c. Tilføj derefter disse sammen.
• Divider resultatet med summen af ​​sidelængderne a, b og c.
• Gentag den samme proces for y-koordinaterne, men brug sidelængderne a, b og c.

Formel i midten af ​​en trekantvinkel

Formlen til at finde midten af ​​en vinkel i en trekant er som følger:

Lad, I en trekant er D, F og G de punkter, hvor vinkelhalveringslinjen for henholdsvis vinklerne A, B og C møder siderne BC, AC og AB.

Vinklen ∠AIB (hvor I er midten af ​​trekanten) kan beregnes ved hjælp af formlen:

∠AIB = 180° – (halvdelen af ​​summen af ​​vinklerne A og B)

ELLER

∠AIB = 180° – (∠A + ∠B)/2

Sådan finder du midten af ​​en trekant

Der er to metoder til at finde midten af ​​en trekant. I konstruktionen lokaliserer vi incenteret ved at tegne trekantens vinkelhalveringslinjer. I koordinatgeometri bruger vi en formel til at bestemme incenteret.

Brug af koordinatgeometri : Find midten af ​​trekanten med koordinaterne angivet som: A(2, 2), B(6, 2) og C(4, 5)

Ifølge de givne oplysninger

• (x₁, og₁) = (2, 2)
• (x₂, og₂) = (6, 2)
• (x₃, og₃) = (4, 5)

Vi ved, at midten af ​​en trekant er:

I(x, y) = {(økse ₁ + bx ₂ + cx ₃ )/(a + b + c), (er ₁ + af ₂ + c ₃ )/(a + b + c)}

For side a: Afstanden mellem punkt B og C = √((6 – 4)²+ (2 – 5)²) = √8

For side b: Afstanden mellem punkt A og C = √((2 – 4)²+ (2 – 5)²) = √13

For side c: Afstanden mellem punkt A og B = √((6 – 2)²+ (2 – 2)²) = 4

Sætter vi værdierne af a, b, c i formlen for incenter, får vi:

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4) )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Midten af ​​trekanten ABC med koordinaterne er (22/5,62/25)

Hvordan konstruerer man midten af ​​en trekant?

For at konstruere midten af ​​en trekant vil det kræve at bruge et kompas. Brug et kompas ved at følge nedenstående trin:

Trin 1: Sæt den ene ende af kompasset på et hjørne af trekanten, og den anden ende rører den ene side.

Trin 2: Brug kompasset til at tegne to buer på to sider af trekanten.

stak java

Trin 3: Med samme afstand på kompasset laver du to buer inde i trekanten. Disse buer skal krydse hinanden, hvorfra de rører siderne.

Trin 4: Tegn en linje fra trekantens toppunkt til hvor de to indvendige buer krydser hinanden.

Trin 5: Gentag de samme trin fra trekantens anden toppunkt.

Trin 6: Hvor de to linjer mødes eller krydser, er trekantens centrum.

Incenter af retvinklet trekant

Incentret hvis en Retvinklet trekant er det punkt, hvor alle halveringslinjerne i en retvinklet trekant mødes. Hvis siderne i en retvinklet trekant måler a, b og c, så er radius af incirkel 'r' givet som r = (ab)/(a + b + c). Midten af ​​den retvinklede trekant er illustreret nedenfor:

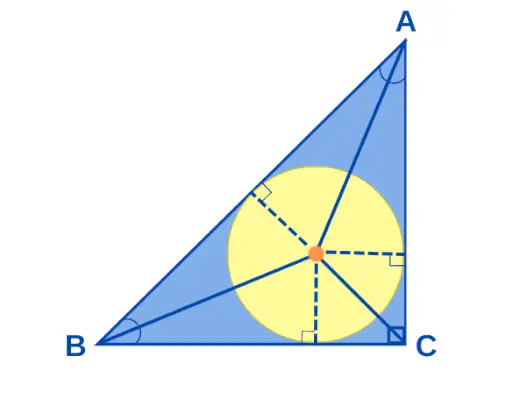
Midten af ​​en retvinklet trekant

Centroid, Circumcenter, Incenter, Orthocenter

Centroid, Circumcenter, Incenter og Orthocenter er de fire vigtige punkter relateret til en traingle. En sammenligning mellem Centroid, Circumcenter, Incenter og Orthocenter er tabel nedenfor:

Tjek også

• Trekantområdet
• Omkreds af trekanten
• Vinkelsum egenskab for en trekant

Eksempler på midten af ​​en trekant

Eksempel 1: Beregn midten af ​​trekant ABC. AB= 8 cm, BC= 15 cm, CA= 17 cm.

Løsning:

Ved at bruge formlen for Incenter of Triangle = (aA + bB + cC)/(a + b + c)

hvor,

• a = 8
• b = 15
• c = 17

Og vinkler er,

• A = 30°
• B = 60°
• C = 90°

Sætter disse værdier i formlen for at få,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Eksempel 2: Jane beregnede arealet af et trekantet felt til 120 kvadratmeter. Markens omkreds er 36 meter. Hvis en cirkel er tegnet inde i trekanten på en måde, så den rører ved hver side af trekanten, skal du hjælpe Jane med at beregne trekantens inradius.

Løsning:

Ifølge de givne oplysninger,

Areal af trekanten = 120 kvadratmeter

Omkreds af trekanten = 36 meter

Vi ved, arealet af en trekant = r × s

s = semiperimeter

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 meter

Øv problemer på midten af ​​en trekant

Opgave 1: Givet trekant PQR med toppunkter P(1, 2), Q(4, 6) og R(7, 2), find koordinaterne for incenteret.

Opgave 2: Konstruer en trekant ABC med ∠A = 45°, ∠B = 60° og ∠C = 75°. Brug byggemetoden til at finde incentret.

Opgave 3: I trekant LMN, hvis ∠L = 75°, ∠M = 60° og ∠N = 45°, skal du finde koordinaterne for midten.

Opgave 4: Konstruer en trekant XYZ med ∠X = 80°, ∠Y = 50° og ∠Z = 50°. Brug byggemetoden til at finde incentret.

Incenter of a Triangle: Ofte stillede spørgsmål

Hvad er midten af ​​en trekant?

Midten af ​​en trekant er det punkt, hvor de indre vinklers halveringslinjer skærer hinanden. Det er lige langt fra alle tre sider af trekanten.

Hvad er betydningen af ​​incentret i en trekant?

Incentret er signifikant, da det er midten af ​​trekantens incirkel, den største cirkel, der passer inde i trekanten. Det har den egenskab, at det er lige langt fra alle sider.

Kan Incenter være uden for trekanten?

Nej, midten er altid inde i trekanten. Det er samtidighedspunktet for vinkelhalveringslinjen, og per definition skal det være inden for trekantens grænser.

Hvordan er Incenter konstrueret ved hjælp af et kompas og lige kant?

For at konstruere incentret skal du bruge et kompas til at tegne vinkelhalveringslinjer fra hvert hjørne til den modsatte side. Incentret er det punkt, hvor disse halveringslinjer skærer hinanden.

Hvad er Incenter Formula?

Formlen for midten af ​​en trekant kan skrives som:

frac{(aA+bB+cC)}{a+b+c}

streng metoder java

Hvad er egenskaberne ved midten af ​​en trekant?

Incentret har nogle nøgleegenskaber. Det er lige langt fra trekantens sider, hvilket betyder, at afstandene til siderne er lige store. Det er også skæringspunktet for vinkelhalveringslinjen, der deler vinklerne i to lige store dele.

Hvordan bestemmes incentret?

For at bestemme incenteret skal du finde, hvor vinkelhalveringslinjerne skærer hinanden. Dette kan gøres ved hjælp af incenterformlen eller ved at tegne vinkelhalveringslinjen og finde deres skæringspunkt.

Hvad er forskellen mellem Incentre og Circumcentre?

Den største forskel mellem incenter og circumcenter er deres fokus. Incenteret omhandler vinkelhalveringslinjer og er centrum af den indskrevne cirkel, mens circumcenter omhandler vinkelrette halveringslinjer og er centrum for den omskrevne cirkel.

Er Incentre og Centroid det samme?

Nej, incenter og tyngdepunkt er forskellige. Incentret er hvor vinkelhalveringslinjer mødes, mens tyngdepunktet er der hvor medianerne skærer hinanden. Medianer forbinder hjørner til midtpunktet af den modsatte side.

Er Incentre og Orthocentre det samme?

Nej, incenter og ortocenter er ikke det samme. Incentret er det punkt, hvor vinklen halverer hinanden, mens ortocentret involverer højder - linjer fra hvert toppunkt vinkelret på den modsatte side. De er forskellige punkter i en trekant.