Givet en simpel udtrykstræ bestående af grundlæggende binære operatorer, dvs. + - * og / og nogle heltal evaluerer udtrykstræet.
Eksempler:
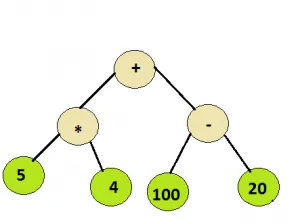
Anbefalet praksis Udtrykstræ Prøv det!Input: Rodknude i nedenstående træ
Produktion: 100
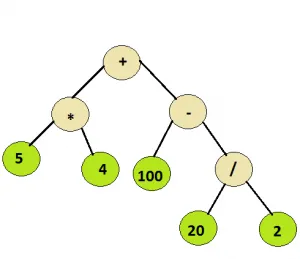
Input: Rodknude i nedenstående træ
forårsstøvlearkitektur
Produktion: 110
Nærme sig: Metoden til at løse dette problem er baseret på følgende observation:
Da alle operatorerne i træet er binære, vil hver node derfor have enten 0 eller 2 børn. Som det kan udledes af eksemplerne ovenfor, vil alle heltalsværdier vises ved bladknuderne, mens de indre knudepunkter repræsenterer operatorerne.
Derfor kan vi gøre uordensgennemgang af det binære træ og evaluer udtrykket, mens vi går videre.
For at evaluere syntakstræet kan en rekursiv tilgang følges.
Algoritme:
- Lad t være syntakstræet
- Hvis t ikke er null, så
- Hvis t.info er operand så
- Returner t.info
- Andet
- A = solve(t.venstre)
- B = solve(t.right)
- return A operator B hvor operator er informationen indeholdt i t
Nedenfor er implementeringen af ovenstående tilgang:
C++// C++ program to evaluate an expression tree #include
// Java program to evaluate expression tree import java.lang.*; class GFG{ Node root; // Class to represent the nodes of syntax tree public static class Node { String data; Node left right; Node(String d) { data = d; left = null; right = null; } } private static int toInt(String s) { int num = 0; // Check if the integral value is // negative or not // If it is not negative generate // the number normally if (s.charAt(0) != '-') for(int i = 0; i < s.length(); i++) num = num * 10 + ((int)s.charAt(i) - 48); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for(int i = 1; i < s.length(); i++) num = num * 10 + ((int)(s.charAt(i)) - 48); num = num * -1; } return num; } // This function receives a node of the syntax // tree and recursively evaluate it public static int evalTree(Node root) { // Empty tree if (root == null) return 0; // Leaf node i.e an integer if (root.left == null && root.right == null) return toInt(root.data); // Evaluate left subtree int leftEval = evalTree(root.left); // Evaluate right subtree int rightEval = evalTree(root.right); // Check which operator to apply if (root.data.equals('+')) return leftEval + rightEval; if (root.data.equals('-')) return leftEval - rightEval; if (root.data.equals('*')) return leftEval * rightEval; return leftEval / rightEval; } // Driver code public static void main(String[] args) { // Creating a sample tree Node root = new Node('+'); root.left = new Node('*'); root.left.left = new Node('5'); root.left.right = new Node('-4'); root.right = new Node('-'); root.right.left = new Node('100'); root.right.right = new Node('20'); System.out.println(evalTree(root)); root = null; // Creating a sample tree root = new Node('+'); root.left = new Node('*'); root.left.left = new Node('5'); root.left.right = new Node('4'); root.right = new Node('-'); root.right.left = new Node('100'); root.right.right = new Node('/'); root.right.right.left = new Node('20'); root.right.right.right = new Node('2'); System.out.println(evalTree(root)); } } // This code is contributed by Ankit Gupta
# Python program to evaluate expression tree # Class to represent the nodes of syntax tree class node: def __init__(self value): self.left = None self.data = value self.right = None # This function receives a node of the syntax tree # and recursively evaluate it def evaluateExpressionTree(root): # empty tree if root is None: return 0 # leaf node if root.left is None and root.right is None: return int(root.data) # evaluate left tree left_sum = evaluateExpressionTree(root.left) # evaluate right tree right_sum = evaluateExpressionTree(root.right) # check which operation to apply if root.data == '+': return left_sum + right_sum elif root.data == '-': return left_sum - right_sum elif root.data == '*': return left_sum * right_sum else: return left_sum // right_sum # Driver function to test above problem if __name__ == '__main__': # creating a sample tree root = node('+') root.left = node('*') root.left.left = node('5') root.left.right = node('-4') root.right = node('-') root.right.left = node('100') root.right.right = node('20') print (evaluateExpressionTree(root)) root = None # creating a sample tree root = node('+') root.left = node('*') root.left.left = node('5') root.left.right = node('4') root.right = node('-') root.right.left = node('100') root.right.right = node('/') root.right.right.left = node('20') root.right.right.right = node('2') print (evaluateExpressionTree(root)) # This code is contributed by Harshit Sidhwa
// C# program to evaluate expression tree using System; public class GFG { // Class to represent the nodes of syntax tree public class Node { public String data; public Node left right; public Node(String d) { data = d; left = null; right = null; } } private static int toInt(String s) { int num = 0; // Check if the integral value is // negative or not // If it is not negative generate // the number normally if (s[0] != '-') for (int i = 0; i < s.Length; i++) num = num * 10 + ((int) s[i] - 48); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for (int i = 1; i < s.Length; i++) num = num * 10 + ((int) (s[i]) - 48); num = num * -1; } return num; } // This function receives a node of the syntax // tree and recursively evaluate it public static int evalTree(Node root) { // Empty tree if (root == null) return 0; // Leaf node i.e an integer if (root.left == null && root.right == null) return toInt(root.data); // Evaluate left subtree int leftEval = evalTree(root.left); // Evaluate right subtree int rightEval = evalTree(root.right); // Check which operator to apply if (root.data.Equals('+')) return leftEval + rightEval; if (root.data.Equals('-')) return leftEval - rightEval; if (root.data.Equals('*')) return leftEval * rightEval; return leftEval / rightEval; } // Driver code public static void Main(String[] args) { // Creating a sample tree Node root = new Node('+'); root.left = new Node('*'); root.left.left = new Node('5'); root.left.right = new Node('-4'); root.right = new Node('-'); root.right.left = new Node('100'); root.right.right = new Node('20'); Console.WriteLine(evalTree(root)); root = null; // Creating a sample tree root = new Node('+'); root.left = new Node('*'); root.left.left = new Node('5'); root.left.right = new Node('4'); root.right = new Node('-'); root.right.left = new Node('100'); root.right.right = new Node('/'); root.right.right.left = new Node('20'); root.right.right.right = new Node('2'); Console.WriteLine(evalTree(root)); } } // This code is contributed by umadevi9616
<script> // javascript program to evaluate expression tree var root; // Class to represent the nodes of syntax tree class Node { constructor(val) { this.data = val; this.left = null; this.right = null; } } function toInt( s) { var num = 0; // Check if the integral value is // negative or not // If it is not negative generate // the number normally if (s.charAt(0) != '-') for (i = 0; i < s.length; i++) num = num * 10 + ( s.charCodeAt(i) - 48); // If it is negative calculate the +ve number // first ignoring the sign and invert the // sign at the end else { for (i = 1; i < s.length; i++) num = num * 10 + (s.charCodeAt(i) - 48); num = num * -1; } return num; } // This function receives a node of the syntax // tree and recursively evaluate it function evalTree(root) { // Empty tree if (root == null) return 0; // Leaf node i.e an integer if (root.left == null && root.right == null) return toInt(root.data); // Evaluate left subtree var leftEval = evalTree(root.left); // Evaluate right subtree var rightEval = evalTree(root.right); // Check which operator to apply if (root.data === ('+')) return leftEval + rightEval; if (root.data === ('-')) return leftEval - rightEval; if (root.data === ('*')) return leftEval * rightEval; return leftEval / rightEval; } // Driver code // Creating a sample tree var root = new Node('+'); root.left = new Node('*'); root.left.left = new Node('5'); root.left.right = new Node('-4'); root.right = new Node('-'); root.right.left = new Node('100'); root.right.right = new Node('20'); document.write(evalTree(root)); root = null; // Creating a sample tree root = new Node('+'); root.left = new Node('*'); root.left.left = new Node('5'); root.left.right = new Node('4'); root.right = new Node('-'); root.right.left = new Node('100'); root.right.right = new Node('/'); root.right.right.left = new Node('20'); root.right.right.right = new Node('2'); document.write('
'+evalTree(root)); // This code is contributed by gauravrajput1 </script>
Produktion
60 110
Tidskompleksitet: O(n), da hver node besøges én gang.
Hjælpeplads: På)