Relationel algebra er et proceduremæssigt forespørgselssprog. Det giver en trin for trin proces for at opnå resultatet af forespørgslen. Det bruger operatører til at udføre forespørgsler.
Typer af relationel operation
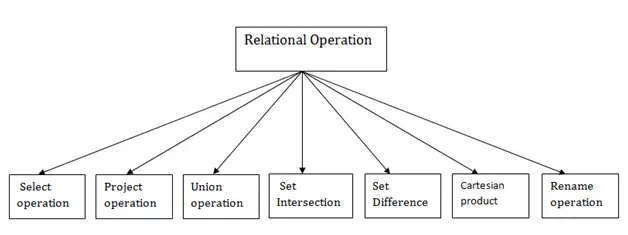
1. Vælg Operation:
- Select-operationen vælger tupler, der opfylder et givet prædikat.
- Det er betegnet med sigma (σ).
Notation: σ p(r)
Hvor:
s bruges til forudsigelse af valg
r bruges til relation
s bruges som en propositionel logikformel, der kan bruge forbindelser som: AND OR og NOT. Disse relationelle kan bruges som relationelle operatorer som =, ≠, ≧, , ≦.
For eksempel: LÅN Relation
| AFDELINGSNAVN | LÅN_NR | BELØB |
|---|---|---|
| Downtown | L-17 | 1000 |
| Redwood | L-23 | 2000 |
| Perryride | L-15 | 1500 |
| Downtown | L-14 | 1500 |
| Mianus | L-13 | 500 |
| Roundhill | L-11 | 900 |
| Perryride | L-16 | 1300 |
Input:
σ BRANCH_NAME='perryride' (LOAN)
Produktion:
int til streng konvertering
| AFDELINGSNAVN | LÅN_NR | BELØB |
|---|---|---|
| Perryride | L-15 | 1500 |
| Perryride | L-16 | 1300 |
2. Projektdrift:
- Denne operation viser listen over de attributter, som vi ønsker skal vises i resultatet. Resten af attributterne er elimineret fra tabellen.
- Det er angivet med ¸.
Notation: ∏ A1, A2, An (r)
Hvor
A1 , A2 , A3 bruges som et attributnavn på relationen r .
Eksempel: KUNDERELATION
| NAVN | GADE | BY |
|---|---|---|
| Jones | Hoved | Harrison |
| Smith | Nord | Rug |
| Hays | Hoved | Harrison |
| Karry | Nord | Rug |
| Johnson | Sjæl | Brooklyn |
| Brooks | Senator | Brooklyn |
Input:
∏ NAME, CITY (CUSTOMER)
Produktion:
| NAVN | BY |
|---|---|
| Jones | Harrison |
| Smith | Rug |
| Hays | Harrison |
| Karry | Rug |
| Johnson | Brooklyn |
| Brooks | Brooklyn |
3. Fagforeningsdrift:
- Antag, at der er to tupler R og S. Unionsoperationen indeholder alle tupler, der enten er i R eller S eller begge i R & S.
- Det eliminerer de dobbelte tupler. Det er angivet med ∪.
Notation: R ∪ S
En fagforeningsdrift skal opfylde følgende betingelse:
- R og S skal have attributten med samme tal.
- Duplikerede tupler elimineres automatisk.
Eksempel:
INDLÆRERELATION
numrene i alfabetet
| KUNDENAVN | ACCOUNT_NR |
|---|---|
| Johnson | A-101 |
| Smith | A-121 |
| Mayes | A-321 |
| Turner | A-176 |
| Johnson | A-273 |
| Jones | A-472 |
| Lindsay | A-284 |
LÅN RELATION
| KUNDENAVN | LÅN_NR |
|---|---|
| Jones | L-17 |
| Smith | L-23 |
| Hayes | L-15 |
| Jackson | L-14 |
| Karry | L-93 |
| Smith | L-11 |
| Williams | L-17 |
Input:
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Produktion:
| KUNDENAVN |
|---|
| Johnson |
| Smith |
| Hayes |
| Turner |
| Jones |
| Lindsay |
| Jackson |
| Karry |
| Williams |
| Mayes |
4. Indstil skæringspunkt:
- Antag, at der er to tupler R og S. Den indstillede skæringsoperation indeholder alle tupler, der er i både R & S.
- Det er angivet med skæringspunktet ∩.
Notation: R ∩ S
Eksempel: Ved at bruge ovenstående INDSÆTNINGSTabel og LÅN-tabellen
Input:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Produktion:
.tif-fil
| KUNDENAVN |
|---|
| Smith |
| Jones |
5. Indstil forskel:
- Antag, at der er to tupler R og S. Den indstillede skæringsoperation indeholder alle tupler, der er i R, men ikke i S.
- Det er angivet med kryds minus (-).
Notation: R - S
Eksempel: Ved at bruge ovenstående INDSÆTNINGSTabel og LÅN-tabellen
Input:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Produktion:
| KUNDENAVN |
|---|
| Jackson |
| Hayes |
| Williams |
| Karry |
6. Kartesisk produkt
- Det kartesiske produkt bruges til at kombinere hver række i en tabel med hver række i den anden tabel. Det er også kendt som et krydsprodukt.
- Det er angivet med X.
Notation: E X D
Eksempel:
MEDARBEJDER
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | Smith | EN |
| 2 | Harry | C |
| 3 | John | B |
AFDELING
| DEPT_NO | DEPT_NAME |
|---|---|
| EN | Markedsføring |
| B | Salg |
| C | gyldige |
Input:
EMPLOYEE X DEPARTMENT
Produktion:
java sortering af en arraylist
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | Smith | EN | EN | Markedsføring |
| 1 | Smith | EN | B | Salg |
| 1 | Smith | EN | C | gyldige |
| 2 | Harry | C | EN | Markedsføring |
| 2 | Harry | C | B | Salg |
| 2 | Harry | C | C | gyldige |
| 3 | John | B | EN | Markedsføring |
| 3 | John | B | B | Salg |
| 3 | John | B | C | gyldige |
7. Omdøb operation:
Omdøb-operationen bruges til at omdøbe outputrelationen. Det er betegnet med rho (p).
Eksempel: Vi kan bruge omdøb-operatoren til at omdøbe STUDENT-relation til STUDENT1.
ρ(STUDENT1, STUDENT)
