Hvad er datastruktur:
En datastruktur er et lager, der bruges til at gemme og organisere data. Det er en måde at arrangere data på en computer, så de kan tilgås og opdateres effektivt.
En datastruktur bruges ikke kun til at organisere dataene. Det bruges også til behandling, hentning og lagring af data. Forskellige grundlæggende og avancerede typer af datastrukturer bruges i næsten alle programmer eller softwaresystemer, der er blevet udviklet. Så vi skal have et godt kendskab til datastrukturer.
Datastrukturer er en integreret del af computere, der bruges til at arrangere data i hukommelsen. De er væsentlige og ansvarlige for at organisere, behandle, få adgang til og gemme data effektivt. Men det er ikke alt. Forskellige typer af datastrukturer har deres egenskaber, funktioner, applikationer, fordele og ulemper. Så hvordan identificerer man en datastruktur, der er egnet til en bestemt opgave? Hvad menes med begrebet 'datastruktur'? Hvor mange typer datastrukturer findes der, og hvad bruges de til?

Hvad er datastruktur: typer, klassifikationer og applikationer
Vi har dækket dig. Vi har lavet en komplet liste over alt om, hvad datastruktur er, hvad er typerne af datastrukturer, klassificeringen af datastrukturer, anvendelserne af hver datastruktur og så videre. I denne artikel vil vi diskutere alle aspekter af hver datastruktur for at hjælpe dig med at vælge den bedste på få minutter.
Indholdsfortegnelse
- Hvad er datastruktur?
- Hvordan varierer datastrukturen fra datatypen?
- Klassificering af datastruktur
- Arrays
- Linket liste
- Stak
- Kø
- Træ
- Kurve
- Konklusion
Hvordan datastruktur varierer fra datatype:
Vi har allerede lært om datastruktur. Mange gange er det, der sker, at folk bliver forvirrede mellem datatype og datastruktur. Så lad os se et par forskelle mellem datatype og datastruktur for at gøre det klart.
| Datatype | Datastruktur |
|---|---|
| Datatypen er formen af en variabel, som en værdi kan tildeles. Den definerer, at den bestemte variabel kun vil tildele værdierne for den givne datatype. | Datastruktur er en samling af forskellige slags data. Alle data kan repræsenteres ved hjælp af et objekt og kan bruges i hele programmet. |
| Det kan indeholde værdi, men ikke data. Derfor er den datafri. | Det kan indeholde flere typer data inden for et enkelt objekt. |
| Implementeringen af en datatype er kendt som abstrakt implementering. amplitudemodulation | Datastrukturimplementering er kendt som konkret implementering. |
| Der er ingen tidskompleksitet i tilfælde af datatyper. | I datastrukturobjekter spiller tidskompleksitet en vigtig rolle. |
| I tilfælde af datatyper gemmes værdien af data ikke, fordi den kun repræsenterer den type data, der kan lagres. | Mens i tilfælde af datastrukturer, får dataene og deres værdi plads i computerens hovedhukommelse. En datastruktur kan også indeholde forskellige typer og typer af data inden for et enkelt objekt. |
| Eksempler på datatyper er int, float, double osv. | Eksempler på datastruktur er stak, kø, træ osv. |
Klassificering af datastruktur:
Datastruktur har mange forskellige anvendelser i vores daglige liv. Der er mange forskellige datastrukturer, der bruges til at løse forskellige matematiske og logiske problemer. Ved at bruge datastruktur kan man organisere og behandle en meget stor mængde data på en relativt kort periode. Lad os se på forskellige datastrukturer, der bruges i forskellige situationer.
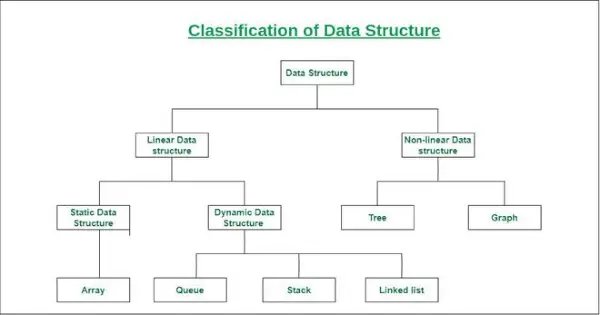
Klassificering af datastruktur
- Lineær datastruktur: Datastruktur, hvor dataelementer er arrangeret sekventielt eller lineært, hvor hvert element er knyttet til dets forrige og næste tilstødende elementer, kaldes en lineær datastruktur.
Eksempler på lineære datastrukturer er matrix, stak, kø, linket liste osv.- Statisk datastruktur: Statisk datastruktur har en fast hukommelsesstørrelse. Det er nemmere at få adgang til elementerne i en statisk datastruktur.
Et eksempel på denne datastruktur er et array. - Dynamisk datastruktur: I den dynamiske datastruktur er størrelsen ikke fast. Det kan opdateres tilfældigt i løbet af kørselstiden, hvilket kan anses for at være effektivt med hensyn til kodens hukommelses- (plads)kompleksitet.
Eksempler på denne datastruktur er kø, stak osv.
- Statisk datastruktur: Statisk datastruktur har en fast hukommelsesstørrelse. Det er nemmere at få adgang til elementerne i en statisk datastruktur.
- Ikke-lineær datastruktur: Datastrukturer, hvor dataelementer ikke er placeret sekventielt eller lineært, kaldes ikke-lineære datastrukturer. I en ikke-lineær datastruktur kan vi ikke krydse alle elementerne i en enkelt kørsel.
Eksempler på ikke-lineære datastrukturer er træer og grafer.
Behov for datastruktur:
Strukturen af dataene og syntesen af algoritmen er i forhold til hinanden. Datapræsentation skal være let at forstå, så udvikleren, såvel som brugeren, kan foretage en effektiv implementering af operationen.
Datastrukturer giver en nem måde at organisere, hente, administrere og gemme data på.
Her er en liste over behov for data.
- Ændring af datastruktur er let.
- Det kræver mindre tid.
- Spar lagerplads.
- Datarepræsentation er let.
- Nem adgang til den store database.
Arrays:
Et array er en lineær datastruktur, og det er en samling af elementer, der er gemt på sammenhængende hukommelsesplaceringer. Ideen er at opbevare flere genstande af samme type sammen på ét sted. Det gør det muligt at behandle en stor mængde data på relativt kort tid. Det første element i arrayet er indekseret med en sænkning på 0. Der er forskellige operationer mulige i et array, f.eks. Søgning, Sortering, Indsættelse, Traversering, Reversering og Sletning.

Array
Karakteristika for et array:
Et array har forskellige karakteristika, som er som følger:
govinda skuespiller
- Arrays bruger en indeksbaseret datastruktur, som hjælper med at identificere hvert af elementerne i et array nemt ved hjælp af indekset.
- Hvis en bruger ønsker at gemme flere værdier af samme datatype, kan arrayet udnyttes effektivt.
- Et array kan også håndtere komplekse datastrukturer ved at lagre data i et todimensionelt array.
- Et array bruges også til at implementere andre datastrukturer som stakke, køer, dynger, Hash-tabeller osv.
- Søgningsprocessen i et array kan udføres meget nemt.
Operationer udført på array:
- Initialisering : Et array kan initialiseres med værdier på tidspunktet for erklæringen eller senere ved hjælp af en tildelingserklæring.
- Adgang til elementer: Elementer i et array kan tilgås ved deres indeks, som starter fra 0 og går op til størrelsen af arrayet minus én.
- Søger efter elementer : Arrays kan søges efter et specifikt element ved hjælp af lineær søgning eller binære søgealgoritmer.
- Sortering af elementer : Elementer i en matrix kan sorteres i stigende eller faldende rækkefølge ved hjælp af algoritmer som boblesortering, indsættelsessortering eller hurtig sortering.
- Indsættelse af elementer: Elementer kan indsættes i et array på et bestemt sted, men denne operation kan være tidskrævende, fordi det kræver at flytte eksisterende elementer i arrayet.
- Sletning af elementer: Elementer kan slettes fra et array ved at flytte de elementer, der kommer efter det, for at udfylde hullet.
- Opdatering af elementer: Elementer i et array kan opdateres eller ændres ved at tildele en ny værdi til et specifikt indeks.
- Gennemgående elementer: Elementerne i et array kan krydses i rækkefølge ved at besøge hvert element én gang.
Disse er nogle af de mest almindelige operationer, der udføres på arrays. De specifikke operationer og algoritmer, der anvendes, kan variere baseret på kravene til problemet og det anvendte programmeringssprog.
Anvendelser af Array:
Forskellige anvendelser af et array er som følger:
- Et array bruges til at løse matrixproblemer.
- Databaseposter implementeres også af et array.
- Det hjælper med at implementere en sorteringsalgoritme.
- Det bruges også til at implementere andre datastrukturer som stakke, køer, dynger, Hash-tabeller osv.
- Et array kan bruges til CPU-planlægning.
- Kan anvendes som opslagstabel i computere.
- Arrays kan bruges i talebehandling, hvor hvert talesignal er et array.
- Computerens skærm vises også af et array. Her bruger vi et multidimensionelt array.
- Arrayet bruges i mange ledelsessystemer som et bibliotek, studerende, parlament osv.
- Arrayet bruges i online billetbestillingssystemet. Kontakter på en mobiltelefon vises af dette array.
- I spil som online skak, hvor spilleren kan gemme sine tidligere træk såvel som nuværende træk. Det indikerer en antydning af position.
- For at gemme billeder i en bestemt dimension i Android Like 360*1200
Real-life applikationer af Array:
- Et array bruges ofte til at gemme data til matematiske beregninger.
- Det bruges i billedbehandling.
- Det bruges også i journalhåndtering.
- Bogsider er også eksempler fra det virkelige liv på en række.
- Det bruges også til bestilling af kasser.
Vil du i gang med arrays? Du kan prøve vores udvalgte artikler og lister for at få den bedste praksis:
- Introduktion til Array Data Structure
- Top 50 Array-kodningsproblemer til interviews
- Øv Array-problem på techcodeview.com
Linket liste:
En sammenkædet liste er en lineær datastruktur, hvor elementer ikke er lagret på sammenhængende hukommelsesplaceringer. Elementerne i en linket liste er linket ved hjælp af pointere som vist på billedet nedenfor:
Typer af linkede lister:
- Enkeltforbundet liste
- Dobbelt linket liste
- Cirkulær linket liste
- Dobbelt cirkulær linket liste

Linket liste
Karakteristika for en linket liste:
En sammenkædet liste har forskellige karakteristika, som er som følger:
- En sammenkædet liste bruger ekstra hukommelse til at gemme links.
- Under initialiseringen af den linkede liste er der ingen grund til at kende størrelsen af elementerne.
- Linkede lister bruges til at implementere stakke, køer, grafer osv.
- Den første knude på den sammenkædede liste kaldes hovedet.
- Den næste pointer i den sidste node peger altid på NULL.
- I en linket liste er indsættelse og sletning let muligt.
- Hver knude på den linkede liste består af en pointer/link, som er adressen på den næste knude.
- Linkede lister kan nemt skrumpes eller vokse på et hvilket som helst tidspunkt.
Operationer udført på linket liste:
En sammenkædet liste er en lineær datastruktur, hvor hver node indeholder en værdi og en reference til den næste node. Her er nogle almindelige handlinger, der udføres på linkede lister:
- Initialisering: En sammenkædet liste kan initialiseres ved at oprette en hovedknude med en reference til den første knude. Hver efterfølgende node indeholder en værdi og en reference til den næste node.
- Indsættelse af elementer: Elementer kan indsættes ved hovedet, halen eller på en bestemt position i den sammenkædede liste.
- Sletning af elementer : Elementer kan slettes fra den sammenkædede liste ved at opdatere referencen for den forrige node til at pege på den næste node, hvilket effektivt fjerner den aktuelle node fra listen.
- Søger efter elementer : Sammenkædede lister kan søges efter et specifikt element ved at starte fra hovedknuden og følge referencerne til de næste knudepunkter, indtil det ønskede element er fundet.
- Opdatering af elementer : Elementer i en sammenkædet liste kan opdateres ved at ændre værdien af en specifik node.
- Gennemgående elementer: Elementerne i en sammenkædet liste kan gennemløbes ved at starte fra hovedknuden og følge referencerne til de næste knudepunkter, indtil slutningen af listen er nået.
- Reversering af en linket liste : Den sammenkædede liste kan vendes ved at opdatere referencerne for hver node, så de peger på den forrige node i stedet for den næste node.
Disse er nogle af de mest almindelige operationer, der udføres på linkede lister. De specifikke operationer og algoritmer, der anvendes, kan variere baseret på kravene til problemet og det anvendte programmeringssprog.
Anvendelser af den linkede liste:
Forskellige anvendelser af linkede lister er som følger:
- Linkede lister bruges til at implementere stakke, køer, grafer osv.
- Sammenkædede lister bruges til at udføre aritmetiske operationer på lange heltal.
- Det bruges til repræsentation af sparsomme matricer.
- Det bruges i den sammenkædede allokering af filer.
- Det hjælper med hukommelseshåndtering.
- Det bruges i repræsentationen af polynomiel manipulation, hvor hvert polynomielt udtryk repræsenterer en node i den sammenkædede liste.
- Linkede lister bruges til at vise billedbeholdere. Brugere kan besøge tidligere, nuværende og næste billeder.
- De bruges til at gemme historikken for den besøgte side.
- De bruges til at udføre fortryd-handlinger.
- Linked bruges i softwareudvikling, hvor de angiver den korrekte syntaks for et tag.
- Linkede lister bruges til at vise sociale medier feeds.
Real-Life-applikationer af en linket liste:
- En sammenkædet liste bruges i Round-Robin-planlægning for at holde styr på tur i multiplayer-spil.
- Det bruges i billedfremviser. De forrige og næste billeder er forbundet, og kan derfor tilgås med forrige og næste knapper.
- I en musikafspilningsliste er sange knyttet til de forrige og næste sange.
Vil du i gang med en linket liste? Du kan prøve vores udvalgte artikler og lister for at få den bedste praksis:
- Introduktion til Linked List Data Structure
- Top 20 linkede liste Interviewspørgsmål
- Øv linket liste-problem på techcodeview.com
Stak:
Stack er en lineær datastruktur, der følger en bestemt rækkefølge, hvori operationerne udføres. Ordren er LIFO (sidst ind først ud) . Det er kun muligt at indtaste og hente data fra den ene ende. Indtastning og hentning af data kaldes også push og pop operation i en stak. Der er forskellige handlinger mulige i en stak som at vende en stak ved hjælp af rekursion, sortering, sletning af det midterste element i en stak osv.

Stak
Karakteristika for en stak:
Stack har forskellige egenskaber, som er som følger:
- Stack bruges i mange forskellige algoritmer som Tower of Hanoi, trægennemgang, rekursion osv.
- Stak implementeres gennem et array eller linket liste.
- Det følger sidst ind først ud operationen, dvs. et element, der indsættes først, vil poppe ind sidst og omvendt.
- Indsættelsen og sletningen udføres i den ene ende, dvs. fra toppen af stakken.
- I stakken, hvis den tildelte plads til stakken er fuld, og stadig nogen forsøger at tilføje flere elementer, vil det føre til stak-overløb.
Anvendelser af stak:
Forskellige anvendelser af Stack er som følger:
- Stakdatastrukturen bruges til evaluering og konvertering af aritmetiske udtryk.
- Det bruges til kontrol af parenteser.
- Mens du vender en streng, bruges stakken også.
- Stack bruges til hukommelseshåndtering.
- Det bruges også til at behandle funktionskald.
- Stakken bruges til at konvertere udtryk fra infix til postfix.
- Stakken bruges til at udføre fortryd- og fortryd-operationer i tekstbehandlingsprogrammer.
- Stakken bruges i virtuelle maskiner som JVM.
- Stakken bruges i medieafspillerne. Nyttigt til at afspille den næste og forrige sang.
- Stakken bruges i rekursionsoperationer.
Operation udført på stak ;
En stak er en lineær datastruktur, der implementerer Last-In-First-Out (LIFO) princippet. Her er nogle almindelige handlinger, der udføres på stakke:
- Skubbe : Elementer kan skubbes op på toppen af stakken, hvilket tilføjer et nyt element til toppen af stakken.
- Pop : Det øverste element kan fjernes fra stakken ved at udføre en pop-operation, der effektivt fjerner det sidste element, der blev skubbet ind på stakken.
- Kig: Topelementet kan inspiceres uden at fjerne det fra stakken ved hjælp af en kig-operation.
- Er tom : Der kan foretages en kontrol for at afgøre, om stakken er tom.
- Størrelse : Antallet af elementer i stakken kan bestemmes ved hjælp af en størrelsesoperation.
Dette er nogle af de mest almindelige operationer, der udføres på stakke. De specifikke operationer og algoritmer, der anvendes, kan variere baseret på kravene til problemet og det anvendte programmeringssprog. Stakke bruges almindeligvis i applikationer såsom evaluering af udtryk, implementering af funktionsopkaldsstakke i computerprogrammer og mange andre.
Virkelige anvendelser af stak:
- Eksempler fra det virkelige liv på en stak er laget af spisetallerkener, der er arrangeret over hinanden. Når du fjerner en plade fra bunken, kan du tage pladen til toppen af bunken. Men det er lige præcis den plade, der senest blev tilføjet til bunken. Hvis du vil have pladen i bunden af bunken, skal du fjerne alle pladerne oven på den for at nå den.
- Browsere bruger stakdatastrukturer til at holde styr på tidligere besøgte websteder.
- Opkaldslog på mobil bruger også stakdatastruktur.
Vil du i gang med Stack? Du kan prøve vores udvalgte artikler og lister for at få den bedste praksis:
java understreng indeholder
- Øv stak-problem på techcodeview.com
Kø:
Kø er en lineær datastruktur, der følger en bestemt rækkefølge, hvori operationerne udføres. Ordren er Først ind først ud (FIFO) dvs. det dataelement, der gemmes først, vil blive tilgået først. Heri sker indtastning og hentning af data ikke kun fra den ene ende. Et eksempel på en kø er enhver kø af forbrugere til en ressource, hvor den forbruger, der kom først, betjenes først. Forskellige operationer udføres på en kø som at vende en kø (med eller uden brug af rekursion), reversere de første K elementer i en kø osv. Et par grundlæggende handlinger udført i kø er kø, kø, foran, bag, osv.
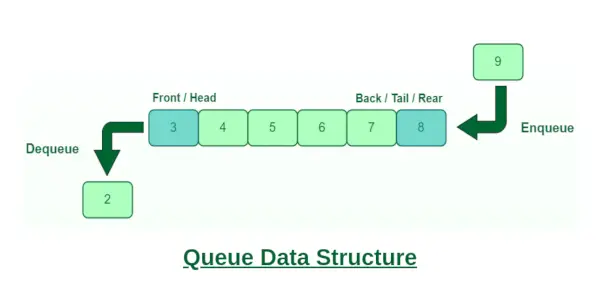
Kø
Karakteristika for en kø:
Køen har forskellige karakteristika, som er som følger:
- Køen er en FIFO-struktur (First In First Out).
- For at fjerne det sidste element i køen skal alle elementer, der er indsat før det nye element i køen, fjernes.
- En kø er en ordnet liste over elementer af lignende datatyper.
Anvendelser af kø:
Forskellige applikationer af kø er som følger:
- Kø bruges til at håndtere webstedstrafik.
- Det hjælper med at vedligeholde afspilningslisten i medieafspillere.
- Kø bruges i operativsystemer til håndtering af afbrydelser.
- Det hjælper med at betjene anmodninger på en enkelt delt ressource, såsom en printer, CPU-opgaveplanlægning osv.
- Det bruges ved asynkron overførsel af data f.eks. rør, fil IO og fatninger.
- Køer bruges til jobplanlægning i operativsystemet.
- I sociale medier bruges køen til at uploade flere billeder eller videoer.
- For at sende en e-mail-kø bruges datastruktur.
- For at håndtere hjemmesidetrafik på et tidspunkt bruges køer.
- I Windows-operativsystemet, for at skifte flere applikationer.
Operation udført i kø:
En kø er en lineær datastruktur, der implementerer First-In-First-Out (FIFO) princippet. Her er nogle almindelige handlinger, der udføres på køer:
- Kø : Elementer kan tilføjes bagerst i køen, hvilket tilføjer et nyt element til slutningen af køen.
- Derfor : Det forreste element kan fjernes fra køen ved at udføre en dequeue-handling, der effektivt fjerner det første element, der blev tilføjet til køen.
- Kig : Frontelementet kan inspiceres uden at fjerne det fra køen ved hjælp af en kig-operation.
- Er tom : Der kan foretages en kontrol for at afgøre, om køen er tom.
- Størrelse : Antallet af elementer i køen kan bestemmes ved hjælp af en størrelsesoperation.
Dette er nogle af de mest almindelige operationer, der udføres på køer. De specifikke operationer og algoritmer, der anvendes, kan variere baseret på kravene til problemet og det anvendte programmeringssprog. Køer bruges ofte i applikationer som planlægning af opgaver, styring af kommunikation mellem processer og mange andre.
Real-Life-applikationer af kø:
- Et eksempel på en kø fra den virkelige verden er en enkeltsporet ensrettet vej, hvor det køretøj, der kommer først ind, kører først ud.
- Et mere virkeligt eksempel kan ses i køen ved billetvinduerne.
- En kasselinje i en butik er også et eksempel på en kø.
- Folk på en rulletrappe
Vil du i gang med Queue? Du kan prøve vores udvalgte artikler og lister for at få den bedste praksis:
- Øvelseskøproblem på techcodeview.com
Træ:
Et træ er en ikke-lineær og hierarkisk datastruktur, hvor elementerne er arrangeret i en trælignende struktur. I et træ kaldes den øverste knude for rodknuden. Hver node indeholder nogle data, og data kan være af enhver type. Den består af en central knude, strukturelle knudepunkter og underknuder, som er forbundet via kanter. Forskellige trædatastrukturer giver hurtigere og nemmere adgang til dataene, da det er en ikke-lineær datastruktur. Et træ har forskellige terminologier som Node, Rod, Edge, Højde på et træ, Grad af et træ osv.
Der er forskellige typer af træ-lignende
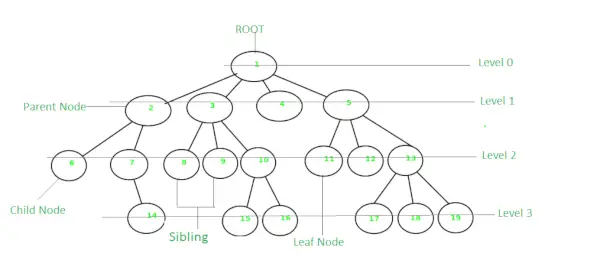
Træ
Karakteristika for et træ:
Træet har forskellige egenskaber, som er som følger:
- Et træ er også kendt som en rekursiv datastruktur.
- I et træ kan rodens højde defineres som den længste vej fra rodknuden til bladknuden.
- I et træ kan man også beregne dybden fra toppen til en hvilken som helst knude. Rodnoden har en dybde på 0.
Anvendelser af træ:
Forskellige anvendelser af Tree er som følger:
- Heap er en trædatastruktur, der implementeres ved hjælp af arrays og bruges til at implementere prioritetskøer.
- B-Tree og B+ Tree bruges til at implementere indeksering i databaser.
- Syntax Tree hjælper med scanning, parsing, generering af kode og evaluering af aritmetiske udtryk i compilerdesign.
- K-D Tree er et rumopdelingstræ, der bruges til at organisere punkter i K-dimensionelt rum.
- Spændende træer bruges i routere i computernetværk.
Operation udført på træet:
Et træ er en ikke-lineær datastruktur, der består af noder forbundet med kanter. Her er nogle almindelige operationer udført på træer:
- Indskud : Nye noder kan tilføjes til træet for at skabe en ny gren eller for at øge træets højde.
- Sletning : Noder kan fjernes fra træet ved at opdatere referencerne for den overordnede node for at fjerne referencen til den aktuelle node.
- Søg : Der kan søges efter elementer i et træ ved at starte fra rodknuden og krydse træet baseret på værdien af den aktuelle knude, indtil den ønskede knude er fundet.
- Traversering : Elementerne i et træ kan krydses på flere forskellige måder, herunder i-ordre, pre-order og post-order traversal.
- Højde : Træets højde kan bestemmes ved at tælle antallet af kanter fra rodknuden til den fjerneste bladknude.
- Dybde : Dybden af en knude kan bestemmes ved at tælle antallet af kanter fra rodknuden til den aktuelle knude.
- Balancering : Træet kan afbalanceres for at sikre, at træets højde minimeres, og fordelingen af noder er så jævn som muligt.
Dette er nogle af de mest almindelige operationer, der udføres på træer. De specifikke operationer og algoritmer, der anvendes, kan variere baseret på kravene til problemet og det anvendte programmeringssprog. Træer bruges almindeligvis i applikationer som søgning, sortering og lagring af hierarkiske data.
Virkelige anvendelser af træ:
- I det virkelige liv hjælper trædatastrukturen i spiludvikling.
- Det hjælper også med at indeksere i databaser.
- Et beslutningstræ er et effektivt maskinlæringsværktøj, der almindeligvis bruges i beslutningsanalyse. Det har en flowchart-lignende struktur, der hjælper med at forstå data.
- Domain Name Server bruger også en trædatastruktur.
- Den mest almindelige anvendelse af et træ er ethvert socialt netværkssted.
Vil du i gang med Tree? Du kan prøve vores udvalgte artikler og lister for at få den bedste praksis:
- Top 50 træinterviewspørgsmål
- Practice Tree problem på techcodeview.com
Kurve:
En graf er en ikke-lineær datastruktur, der består af knudepunkter (eller noder) og kanter. Den består af et begrænset sæt af hjørner og sæt kanter, der forbinder et par knudepunkter. Grafen bruges til at løse de mest udfordrende og komplekse programmeringsproblemer. Det har forskellige terminologier som er sti, grad, tilstødende hjørner, forbundne komponenter osv.
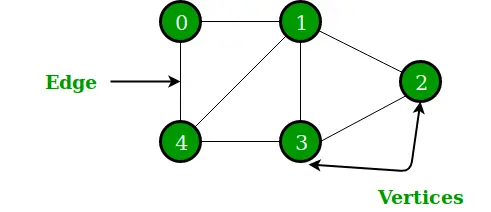
Kurve
Karakteristika for graf:
Grafen har forskellige karakteristika, som er som følger:
- Den maksimale afstand fra et toppunkt til alle de andre toppunkter betragtes som excentriciteten af det toppunkt.
- Toppunktet med minimum excentricitet betragtes som det centrale punkt på grafen.
- Minimumsværdien af excentricitet fra alle hjørner betragtes som radius af en forbundet graf.
Anvendelser af graf:
Forskellige anvendelser af grafer er som følger:
- Grafen bruges til at repræsentere strømmen af beregninger.
- Det bruges til at modellere grafer.
- Operativsystemet bruger Ressourceallokeringsgraf.
- Bruges også på World Wide Web, hvor websiderne repræsenterer noderne.
Operation udført på Graph:
En graf er en ikke-lineær datastruktur bestående af noder og kanter. Her er nogle almindelige handlinger, der udføres på grafer:
- Tilføj vertex: Nye hjørner kan tilføjes til grafen for at repræsentere en ny knude.
- Tilføj kant: Kanter kan tilføjes mellem hjørner for at repræsentere et forhold mellem noder.
- Fjern Vertex : Hjørner kan fjernes fra grafen ved at opdatere referencerne for tilstødende knudepunkter for at fjerne referencen til det aktuelle knudepunkt.
- Fjern Edge : Kanter kan fjernes ved at opdatere referencerne for de tilstødende hjørner for at fjerne referencen til den aktuelle kant.
- Dybde-første søgning (DFS) : En graf kan gennemløbes ved hjælp af en dybde-først-søgning ved at besøge hjørnerne på en dybde-først måde.
- B readth-First Search (BFS): En graf kan krydses ved at bruge en bredde-først-søgning ved at besøge hjørnerne på en bredde-først måde.
- Korteste vej: Den korteste vej mellem to hjørner kan bestemmes ved hjælp af algoritmer såsom Dijkstras algoritme eller A* algoritme.
- Tilsluttede komponenter : De forbundne komponenter i en graf kan bestemmes ved at finde sæt af hjørner, der er forbundet med hinanden, men ikke til andre hjørner i grafen.
- Cyklus detektion : Cykler i en graf kan detekteres ved at kontrollere for bagkanter under en dybde-første søgning.
Dette er nogle af de mest almindelige operationer, der udføres på grafer. De specifikke operationer og algoritmer, der anvendes, kan variere baseret på kravene til problemet og det anvendte programmeringssprog. Grafer bruges almindeligvis i applikationer som computernetværk, sociale netværk og routingproblemer.
Real-life applikationer af graf:
- Et af de mest almindelige eksempler på en graf i den virkelige verden er Google Maps, hvor byer er placeret som hjørner, og stier, der forbinder disse hjørner, er placeret som kanter på grafen.
- Et socialt netværk er også et virkeligt eksempel på en graf, hvor hver person på netværket er en knude, og alle deres venskaber på netværket er kanten af grafen.
- En graf bruges også til at studere molekyler i fysik og kemi.
Vil du i gang med Graph? Du kan prøve vores udvalgte artikler og lister for at få den bedste praksis:
eksempler på Moore maskine
- Introduktion til grafdatastruktur
- Top 50 Graph Interview Spørgsmål
- Practice Graph problem på techcodeview.com
Fordele ved datastruktur:
- Forbedret dataorganisering og lagringseffektivitet.
- Hurtigere datahentning og manipulation.
- Letter design af algoritmer til løsning af komplekse problemer.
- Letter opgaven med at opdatere og vedligeholde data.
- Giver en bedre forståelse af sammenhængen mellem dataelementer.
Ulempen ved datastruktur:
- Øget beregnings- og hukommelsesomkostninger.
- Vanskeligheder ved at designe og implementere komplekse datastrukturer.
- Begrænset skalerbarhed og fleksibilitet.
- Kompleksitet i debugging og test.
- Vanskeligheder ved at ændre eksisterende datastrukturer.
Reference:
Datastrukturer kan findes i forskellige computervidenskabelige lærebøger og onlineressourcer. Nogle populære tekster inkluderer:
- Introduktion til algoritmer af Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest og Clifford Stein.
- Datastrukturer og algoritmeanalyse i Java af Mark Allen Weiss.
- The Algorithm Design Manual af Steven S. Skiena.
- Onlineressourcer som Coursera, Udemy og Khan Academy tilbyder også kurser om datastrukturer og algoritmer.
Konklusion
Selvom det er de mest kendte og brugte datastrukturer, er der også nogle andre former for datastrukturer, som bruges i datalogi, som f.eks. politikbaserede datastrukturer , osv. Men uanset hvilken datastruktur du vælger, har hver enkelt sine fordele og ulemper, uden kendskab til hvilke, kan det være meget dyrt at vælge den forkerte type datastruktur. Så det er meget vigtigt at forstå behovet for situationen og derefter beslutte, hvilken slags datastruktur der passer bedst til jobbet.
