COTANGENS FORMEL

Trigonometri er en vigtig gren af matematikken, der beskæftiger sig med forholdet mellem længderne af sider og vinkler i en retvinklet trekant. Sinus, Cosinus, tangent, cosecant, sekant og cotangens er de seks trigonometriske forhold eller funktioner. Hvor et trigonometrisk forhold er afbildet som forholdet mellem siderne i en retvinklet trekant.

sin θ = modsatte side/hypotenuse
cos θ = tilstødende side/hypotenuse
tan θ = modsat side/tilstødende side
cosec θ = 1/sin θ = hypotenuse/modsat side
sek θ = 1/cos θ = hypotenuse/tilstødende side
barneseng θ = 1/tan θ = tilstødende side/modstående side

En cotangensfunktion er en gensidig funktion af den givne tangentfunktion. Værdien af en cotangens vinkel i en retvinklet trekant er forholdet mellem længden af den side, der støder op til den givne vinkel, og længden af den side, der er modsat den givne vinkel. Vi skriver cotangens funktion som barneseng.

Trekant ABC

Nu er cotangensformlen for vinklen θ,

barneseng θ = (tilstødende side)/(modsat side)

Cotangensfunktionen er positiv i første og tredje kvadrant og negativ i anden og fjerde kvadrant.

barneseng (2π + θ) = barneseng θ (1^stkvadrant)
barneseng (π – θ) = – barneseng θ (2^ndkvadrant)
barneseng (π + θ) = barneseng θ (3^rdkvadrant)
tremmeseng (2π – θ) = – tremmeseng θ (4^thkvadrant)

Cotangensfunktionen er en negativ funktion, da cotangensen af en negativ vinkel er den negative af en cotangens positiv vinkel.

barneseng (-θ) = – barneseng θ

Med hensyn til tangentfunktionen skrives cotangensfunktionen som,

barneseng θ = 1/tan θ

(eller)

barneseng θ = tan (90° – θ) (eller) tan (π/2 – θ)

Cotangensfunktionen i form af sinus- og cosinusfunktioner kan skrives som,

cot θ = cos θ/sin θ

Vi ved, at barneseng θ = tilstødende side/modsatte side

Divider nu både tæller og nævner med hypotenusen

⇒ barneseng θ = (tilstødende side/hypotenuse) / (modsat side/hypotenuse)

Vi ved, at sin θ = modsatte side/hypotenuse

cos θ = tilstødende side/hypotenuse

Derfor er cot θ = cos θ/sin θ

Cotangens funktion i form af sinusfunktion kan skrives som,

barneseng θ = (√1 – sin ² i)/sin i

Vi ved, at cot θ = cos θ/sin θ
greatandhra

Fra de pythagoræiske identiteter har vi;

cos²θ + sin²θ = 1

⇒ cos θ = √1 – sin²jeg

Derfor er barneseng θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Cotangens funktion i form af cosinus funktion kan skrives som,

cot θ = cos θ/(√1 -cos ² jeg)

Vi ved, at cot θ = cos θ/sin θ

Fra de pythagoræiske identiteter har vi;

cos²θ + sin²θ = 1

sin θ = √1 – cos²jeg

Derfor er barneseng θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Cotangensfunktion i form af sekant- og cosekantfunktioner kan skrives som,

cot θ = cosec θ/sek θ
sanjay dutt og

Vi har, cot θ = cos θ/sin θ

Dette kan skrives som, cot θ = (1/sin θ) / (1/cos θ)

⇒ barneseng θ = cosec θ/sek θ

Cotangens funktion i form af cosecant funktion kan skrives som:

barneseng θ = √(kossek ² - 1)

Fra de pythagoræiske identiteter har vi,

cosec²θ – barneseng²θ = 1

⇒ barneseng²θ = 1 – cosec²- 1

Derfor er barneseng θ = √(cosec²- 1)

Cotangens funktion med hensyn til sekantfunktion kan skrives som:

barneseng θ = 1/(√sek ² i – 1)

Fra de pythagoræiske identiteter har vi,

sek²θ – altså²θ = 1

tan θ = √sek²i – 1

Vi ved, at cot θ = 1/tan θ

Derfor, barneseng θ = $frac{1}{sqrt{left(1-sek^{2} heta ight)}}$

Trigonometrisk forholdstabel

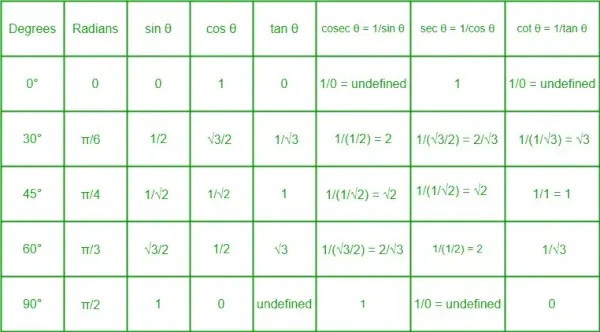
Trigonometrisk forholdstabel

Cotangens lov eller lov om cotangens

Cotangens-loven ligner sinusloven, men her involverer den halve vinkler. Loven om cotangens beskriver forholdet mellem længderne af trekantens sider og cotangenserne af halvdelene af de tre vinkler. Betragt en trekant ABC, hvor a, b og c er længderne af trekantens sider.

Cotangensloven siger, at

$frac{barneseng(frac{A}{2})}{(s-a)} = frac{barneseng(frac{B}{2})}{(s-b)} = frac{barneseng(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Hvor s er halvperimeteren af trekanten ABC, og r er dens inradius af trekantens indskrevne cirkel.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Prøveproblemer

Opgave 1: Find værdien af cot θ hvis tan θ = 3/4.

Løsning:

Givet data, tan θ = 3/4

Vi ved det, barneseng θ = 1/tan θ

⇒ barneseng θ = 1/(3/4) = 4/3

Så barneseng θ = 4/3

Opgave 2: Find værdien af cot α, sin α = 1/3 og cos α = 2√2/3.

streng java indeholder

Løsning:

Givet data, sin α = 1/3 og cos α = 2√2/3

Vi ved det, cot α = cos α/sin α

⇒ barneseng α = (2√2/3) / (1/3) = 2√2

Derfor er værdien af barneseng α = 2√2

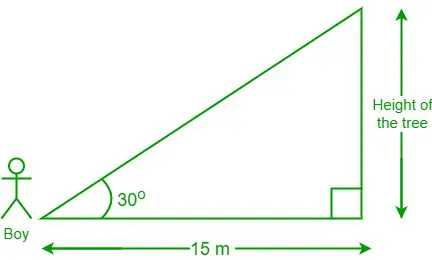
Opgave 3: En dreng, der står 15 m fra et træ, ser i en 30-graders vinkel til toppen af træet. Hvad er højden på træet?

Løsning:

Diagram fra de givne data

Givet data er afstanden mellem drengen og foden af træet = 15 m og θ = 30°

Lad træets højde være 'h'

Vi har, barneseng θ = tilstødende side/modstående side

⇒ tremmeseng 30° = 15/t

⇒ √3 = 15/h [da, tremmeseng 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Derfor er træets højde = 5√3 m

Opgave 4: Find værdien af barneseng x hvis sek x = 6/5.

Løsning:

Givet data, sek x = 6/5

Vi har, sek ² x – altså ² x = 1

⇒ (6/5)²- så²x = 1

⇒ 36/25 – så²x = 1

⇒ altså²x = 36/25 – 1

⇒ altså²x = 11/25

⇒ tan x = √(11/25) = √11/5

Vi ved det, tremmeseng x = 1/tan x

⇒ tremmeseng x = 1/(√11/5) = 5/√11

Derfor er tremmeseng x = 5/√11

Opgave 5: Find værdien af cot θ hvis cosec θ = 25/24.

Løsning:

Givet data, cosec θ = 25/24
burak ozcivit

Vi ved det, barneseng θ = √(kossek ² - 1)

⇒ barneseng θ = √(25/24)²- 1

⇒ tremmeseng θ =√(625 – 576)/576 = √49/576

⇒ barneseng θ = 7/24

Derfor er værdien af barneseng θ = 7/24

Opgave 6: Find værdien af cot β, hvis sin β = 5/13.

Løsning:

Givet data, sin β = 5/13

Vi ved det, uden ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ barneseng β = 12/5

Derfor er værdien af barneseng β = 12/5
streng sammenlignet med java

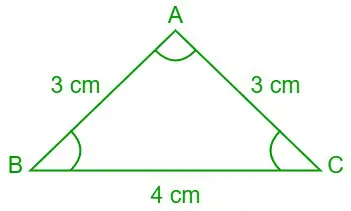
Opgave 7: Brug loven om cotangenter, find værdierne af ∠A, ∠B og ∠C (i grader), hvis længderne af de tre sider af trekanten ABC er a = 4 cm, b= 3 cm og c= 3 cm.

Løsning:

Givet, a = 4 cm, b = 3 cm og c = 3 cm

Trekant ABC

Fra cotangensloven,

$frac{barneseng(frac{A}{2})}{(s-a)} = frac{barneseng(frac{B}{2})}{(s-b)} = frac{barneseng(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Nu er s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Inradius af trekanten r = 2/√5

Fra ligningen af lov om cotangenter,

barneseng (A/2)/1 = 1/(2/√5)

⇒ tremmeseng (A/2) = √5/2 ⇒ A/2 = tremmeseng^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

barneseng(B/2)/2 = 1/(2/√5)

⇒ tremmeseng(B/2)/2 = √5/2 ⇒ tremmeseng (B/2) = √5

⇒ (B/2) = barneseng^-1(√5) = 24,1° ⇒ ∠B = 48,2°

barneseng (C/2)/2 = 1/(2/√5)

⇒ tremmeseng(C/2) = √5 ⇒ (C/2) = tremmeseng^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Derfor er vinklerne for trekanten ABC ∠A = 83,6°, ∠B = 48,2° og ∠C = 48,2°.