Spand sortering er en sorteringsteknik, der involverer opdeling af elementer i forskellige grupper, eller spande. Disse spande er dannet ved ensartet fordeling af elementerne. Når elementerne er opdelt i spande, kan de sorteres ved hjælp af en hvilken som helst anden sorteringsalgoritme. Til sidst samles de sorterede elementer sammen på en ordnet måde.
Spandsorteringsalgoritme:
skab n tomme buckets (eller lister), og gør følgende for hvert array-element arr[i].
- Indsæt arr[i] i bucket[n*array[i]]
- Sorter individuelle spande ved hjælp af indføringssortering.
- Sammenkæd alle sorterede spande.
Hvordan fungerer Bucket Sort?
For at anvende spandsortering på input-arrayet [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , følger vi disse trin:
Trin 1: Opret et array af størrelse 10, hvor hver spalte repræsenterer en spand.

Oprettelse af spande til sortering
Trin 2: Indsæt elementer i buckets fra input-arrayet baseret på deres rækkevidde.
Indsættelse af elementer i spandene:
Java eksempel programmer
- Tag hvert element fra input-arrayet.
- Multiplicer elementet med størrelsen af bucket-arrayet (10 i dette tilfælde). For eksempel, for element 0,23, får vi 0,23 * 10 = 2,3.
- Konverter resultatet til et heltal, som giver os bucket-indekset. I dette tilfælde konverteres 2,3 til hele tallet 2.
- Indsæt elementet i spanden svarende til det beregnede indeks.
- Gentag disse trin for alle elementer i input-arrayet.
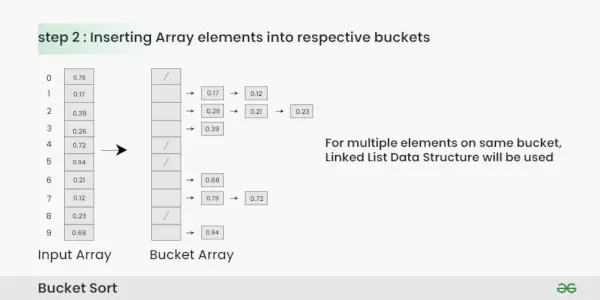
Indsættelse af Array-elementer i respektive spande
Trin 3: Sorter elementerne i hver spand. I dette eksempel bruger vi quicksort (eller en hvilken som helst stabil sorteringsalgoritme) til at sortere elementerne i hver spand.
Sortering af elementerne i hver spand:
- Anvend en stabil sorteringsalgoritme (f.eks. boblesortering, fletsortering) for at sortere elementerne i hver spand.
- Elementerne i hver spand er nu sorteret.
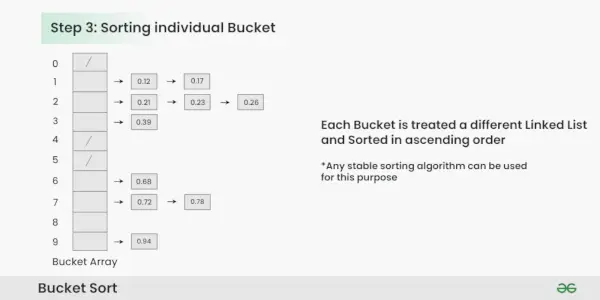
Sortering af individuel spand
Trin 4: Saml elementerne fra hver spand og sæt dem tilbage i det originale array.
Indsamling af elementer fra hver spand:
- Gentag gennem hver spand i rækkefølge.
- Indsæt hvert enkelt element fra spanden i det originale array.
- Når et element er kopieret, fjernes det fra bøtten.
- Gentag denne proces for alle spande, indtil alle elementer er blevet samlet.
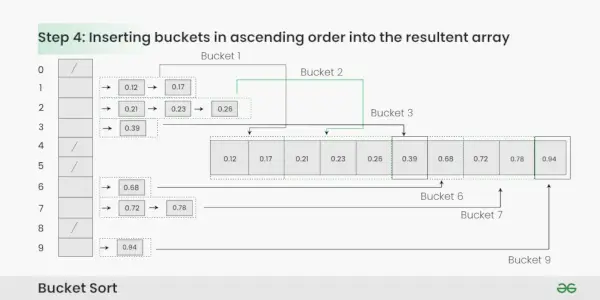
Indsættelse af spande i stigende rækkefølge i det resulterende array
Trin 5: Det originale array indeholder nu de sorterede elementer.
Det endelige sorterede array ved brug af spandsortering for det givne input er [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Returner det sorterede array
Implementering af Bucket Sort Algorithm:
Nedenfor er implementeringen af Bucket Sort:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& bucket) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && spand[j]> nøgle) { spand[j + 1] = spand[j]; j--; } spand[j + 1] = nøgle; } } // Funktion til at sortere arr[] af størrelse n ved hjælp af bucket sort void bucketSort(float arr[], int n) { // 1) Opret n tomme buckets vektorb[n]; // 2) Sæt array-elementer i forskellige buckets for (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listspand) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> key) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, nøgle); } } // Funktion til at sortere arr[] af størrelse n ved hjælp af bucket sort public static void bucketSort(float[] arr) { int n = arr.length; // 1) Opret n tomme buckets List[] buckets = ny ArrayList[n]; for (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 og spand[j]> nøgle: spand[j + 1] = spand[j] j -= 1 spand[j + 1] = nøgle def bucket_sort(arr): n = len(arr) spande = [[] for _ i område(n)] # Sæt array-elementer i forskellige buckets for num i arr: bi = int(n * num) buckets[bi].append(num) # Sorter individuelle buckets ved hjælp af insertion sort for bucket in buckets: insertion_sort (spand) # Sammenkæd alle spande i arr[] indeks = 0 for spand i spande: for antal i spand: arr[indeks] = antal indeks += 1 arr = [0.897, 0.565, 0.656, 0.1234, 0.6345, 40. (arr) print('Sorteret array er:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listspand) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && spand[j]> nøgle) { spand[j + 1] = spand[j]; j--; } spand[j + 1] = nøgle; } } // Funktion til at sortere arr[] af størrelse n ved hjælp af bucket sort static void BucketSort(float[] arr) { int n = arr.Length; // 1) Opret n tomme buckets List[] spande = ny liste[n]; for (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Sæt array-elementer i forskellige buckets for (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && spand[j]> nøgle) { spand[j + 1] = spand[j]; j--; } spand[j + 1] = nøgle; } } funktion bucketSort(arr) { lad n = arr.længde; lad buckets = Array.from({længde: n}, () => []); // Sæt array-elementer i forskellige buckets for (lad i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Produktion
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Kompleksitetsanalyse af Bucket Sort Algorithm:
Tidskompleksitet: På2),
mylivecricket.
- Hvis vi antager, at indsættelse i en spand tager O(1) tid, tager trin 1 og 2 i ovenstående algoritme klart O(n) tid.
- O(1) er let muligt, hvis vi bruger en linket liste til at repræsentere en bucket.
- Trin 4 tager også O(n) tid, da der vil være n elementer i alle spande.
- Det vigtigste trin at analysere er trin 3. Dette trin tager også O(n) tid i gennemsnit, hvis alle tal er ensartet fordelt.
Hjælpeplads: O(n+k)
