Hastighed er simpelthen som du kender et mål for, hvor hurtigt eller langsomt et objekt bevæger sig, ligesom hvor hurtigt du kører en bil. Nu, her taler vi om en bestemt type hastighed. Vinkelhastighed er kun en type hastighed, men her skal kroppen bevæge sig i en cirkulær bane.
Vinkelhastighedsformel
Vinkelhastighed er defineret som hastigheden for ændring af vinkelforskydning, det vil sige den vinkel, som et legeme gennemløber langs en cirkulær bane. Vinkelhastigheden beregnes i form af et antal rotationer/omdrejninger foretaget af et legeme til den tid, det tager. Vinkelhastighed er angivet med græsk bogstav, 'ω' kendt som Omega. SI-enheden for vinkelhastighed er rad/s.
Vinkelhastigheden beregnes ved hjælp af to forskellige formler,
- ω = θ/t ω = v/r
Formel afledning
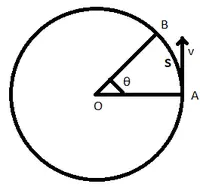
Lad os betragte et legeme, der bevæger sig i en cirkulær bane med radius r vist ovenfor med en lineær hastighed v. Lad os antage, at kroppen bevæger sig fra punkt A til B, der dækker en afstand s gennem cirkelbuen og krydser en vinkel θ i tidsperioden t.
Cirkulær sti dækket af en krop
Vinkelhastigheden er som bekendt hastigheden af ændring af forskydning - Vinkelhastighed, ω = θ/t
Så formlen for vinkelhastighed er ω = θ/t .
En anden formel for vinkelhastighed
På trods af den ovenfor anførte formel er der en anden og mere udbredt formel til beregning af vinkelhastighed ud fra et konkurrencemæssigt synspunkt.
Som ω = θ/t ⇢ (1)
Nu ved vi, at afstanden flyttet hen over en cirkelbue er lig med radius gange vinkel gennemløbet. Så,
s = rθ
=> θ = s/r ⇢ (2)
java char til heltalFra (1) og (2),
ω = s/(rt) ⇢ (3)
Også fra generel forståelse af lineære hastigheder,
v = s/t ⇢ (4)
Fra (3) og (4),
ω = v/r
Prøveproblemer
Spørgsmål 1: Overvej et legeme, der bevæger sig langs en cirkulær bane med en radius på 5m. Den dækker halv omdrejning på 5s. Beregn dens vinkelhastighed.
Løsning:
I halv omdrejning er den gennemløbne vinkel 180 grader. I radianer er det lig med π radianer.
ω = θ/t
=> ω = π/5 = 0,628 rad/s
Spørgsmål 2: Et bilhjul med en radius på 2m roterer med en lineær hastighed på 10m/s. Beregn dens vinkelhastighed.
Løsning:
ω = v/r
ω = 10/2
= 5 rad/s
Spørgsmål 3: Overvej en racerbil, der kører på en cirkulær bane med en hastighed på 18 km/t, og banens radius er 0,2 m. Beregn bilens vinkelhastighed.
Løsning:
v = 18 km/t = 5 m/s
r = 0,2 m
ω = v/r
= 5/0,2
= 25 rad/s
Spørgsmål 4: En bil bevæger sig langs en cirkulær bane med en radius på 2m med en vinkelhastighed på 2 rad/s. Beregn vinklen i grader, som bilen bevæger sig igennem i 2s.
Løsning:
givet, ω = 2 rad/s og t = 2s
Da ω = θ/t => θ = ωt
=> θ = (2 × 2) = 4 rad
I grader er θ = 4 × (180/π) = 229,18 grader
Spørgsmål 5: Hvor mange omdrejninger lavede et legeme ved at bevæge sig langs en cirkulær bane med en vinkelhastighed på 7π rad/s på 0,5s?
Løsning:
Givet ω = 7π rad/s og t = 0,5s
Da ω = θ/t => θ = ωt
θ = (7π × 0,5) = 3,5π
I 2π rad er de dækkede omdrejninger 1
=> I 1 rad er den dækkede omdrejning (1/2π)
=> I 3,5π rad er omdrejninger = 3,5π/2π = 1,75 omdrejninger
Så kroppen vil gennemføre 1 komplet omdrejning og 3/4 af næste omdrejning i en tidsperiode på 0,5 s.
Spørgsmål 6: Hvad vil vinkelhastigheden være for et legeme, der bevæger sig i en cirkulær bane med radius 2m, som dækker 4m buelængde 5s.
Løsning:
Givet s = 4m, r = 2m, t = 5s
Brug formlen s = rθ => θ = s/r
θ = 4/2 = 2 rad
Da ω = θ/t
unix vs windows=> ω = 2/5 = 0,4 rad/s