Nuller af et polynomium er disse reelle, imaginære eller komplekse værdier, når de sættes i polynomiet i stedet for en variabel, bliver resultatet nul (som navnet også antyder nul). Polynomier bruges til at modellere nogle fysiske fænomener, der sker i det virkelige liv, de er meget nyttige til at beskrive situationer matematisk.

Nullerne i et polynomium er alle de x-værdier, der gør polynomiet lig nul. Nuller i et polynomium fortæller os om x-skæringspunkterne i polynomiets graf. I denne artikel vil vi diskutere om nuller af et polynomium, hvordan man finder dem, faktorsætningen osv.

Indholdsfortegnelse

• Hvad er nuller af polynomier?
• Nuller af polynomisk formel
• Hvordan finder man nul af et polynomium?
• For lineært polynomium
• For kvadratisk polynomium
• For kubisk polynomium
• Faktorsætning
• Forholdet mellem nuller og koefficient
• Forholdet mellem nuller og koefficient for andengradsligning
• Forholdet mellem nuller og koefficient for kubikligning
• Dannelse af ligning med nuller af polynomium
• Nuller i grafen over polynomier
• Grundlæggende sætning for lineær algebra
• En rods mangfoldighed
• Artikler relateret til Zeros of Polynomial
• Prøveproblemer på nuller af polynomium
• Øv opgaver på nuller af polynomium

Hvad er nuller af polynomier?

For et polynomium P(x) siger vi, at x = a er polynomiets nul, hvis P(a) = 0, og alle sådanne nuller i et polynomium kaldes almindeligvis nuller i et polynomium. Overvej f.eks. f(x) = 3x – 12. Sæt nu x = 4 i polynomiet, dvs. f(4) = 3×4 – 12 = 0. Således er x = 4 et nul af polynomiet f( x) = 3x – 12.

Eksempel: For f(x) = x ³ – 6x ² + 11x – 6, er x = 1 nul?

Løsning:

For at kontrollere, om hvis x = 1 er nul af f(x) = x³– 6x²+ 11x – 6 eller ej, indsæt x = 1 tommer (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Således er x = 1 et nul af f(x).

Nuller af polynomisk formel

For et lineært polynomium med formen ax + b er dets nul givet ved x = -b/a.

For et kvadratisk polynomium af form akse²+ bx + c, dens nul er givet ved x = {- b ± √D}/2a hvor D er Diskriminerende givet ved b²– 4 ac.

Hvordan finder man nul af et polynomium?

Vi kan finde nullerne i polynomiet for forskellige typer polynomier ved hjælp af forskellige metoder, som er beskrevet nedenfor.

• For lineært polynomium
• For kvadratisk polynomium
• For kubisk polynomium

For lineært polynomium

For lineære polynomier er det nemmeste at finde nul. da der kun er ét nul, og det kan også beregnes ved simpel omarrangering af polynomiet efter ligningspolynomiet til 0.

Find for eksempel nul for lineært polynomium f(x) = 2x – 7.

Løsning:

For at finde nul af f(x), lig f(x) med 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

For kvadratisk polynomium

Der er forskellige metoder til at finde rødder eller nuller af et andengradspolynomium, såsom at opdele mellemleddet, en andengradsformel, som også er kendt som Shree Dharacharya-formlen, og udfylde kvadratet, som ligner den andengradsformel, da andengradsformlen kommer fra færdiggørelsen af ​​kvadratet for den generelle andengradsligning.

Lær mere om løsning af andengradsligninger eller polynomier og hvordan man løser dem. De følgende eksempler viser metoden til at finde nuller af kvadratiske polynomier i detaljer.

Eksempel 1: Find ud af nullerne for P(x) = x ² + 2x – 15.

Svar:

x²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

forberede sig til test mockito

⇒ x = 3, -5

Eksempel 2: Find ud af nuller for P(x) = x ² – 16x + 64.

Svar:

x²– 16x + 64 = 0

Sammenligning med økse²+ bx + c = 0,

vi får, a = 1, b = -16 og c = 64.

Dermed,

⇒ x = 8, 8

For kubisk polynomium

For at finde kubiske nuller er der mange måder, såsom rationel rodsætning og lang division sammen. En metode til at finde rødder af kubisk eller et hvilket som helst højere grads polynomium er som følger:

Trin 1: Brug den rationelle rodsætning til at finde de mulige rødder. dvs., hvis et polynomium har en rationel rod, skal det være divisionen af ​​p/q, hvor p er heltalskonstanten og q er den førende koefficient.

Trin 2: Når du har fundet én rod, skal du dividere polynomiet med faktoren dannet af denne rod ved at bruge lang division og skrive polynomiet som et produkt af kvotient og udbytte.

Trin 3: Hvis kvotienten er et kvadratisk udtryk, løses det ved de ovennævnte metoder for kvadratiske polynomier. Hvis ikke et polynomium på en grad 2, så gentag trin 1 og 2, indtil kvotienten bliver et polynomium med grad 2.

Trin 4: Resultatet af trin 3 er de nødvendige faktorer, og ved at sidestille faktoren med 0, kan vi finde nullerne i polynomiet.

Eksempel: Find nullerne i det kubiske polynomium p(x) = x ³ + 2x ² – 5x – 6.

Løsning:

p(x) = x³+ 2x²– 5x – 6

Som p/q = -6

Ved rationel rodsætning er alle mulige rationelle rødder af polunomialet divisorer af p/q.

Divisorer = ±1, ±2, ±3, ±6

x = -1, i p(x), får vi

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Ved faktorsætning er x + 1 altså faktoren for p(x).

Altså x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

For nuller er p(x) = 0,

Nullpunkter for p(x) er x = -1, x = 2 og x = -3.

Faktorsætning

For polynomiet P(x) siger faktorsætningen, at hvis x =a er nul af P(X) hvis x – er a en faktor af P(x). dvs. begge de følgende betingelser bør holde stik.

• Hvis a er et nul af P(x), vil x−a være en faktor af P(x)
• Hvis x−a er en faktor af P(x), så vil a være et nul af P(x)

Dette kan verificeres ved at se på tidligere eksempler. Faktorsætning kan føre til nogle interessante resultater, som er som følger:

Resultat 1: Hvis P(x) er et polynomium af grad n, og r er et nul af P(x), så kan P(x) skrives på følgende form:

P(x) = (x – r) Q(x)

Hvor Q(x) er et polynomium af grad n-1 og kan findes ved at dividere P(x) med (x – r).

Resultat 2: Hvis P(x) = (x-r)Q(x) og x = t er et nul af Q(x), så vil x = t også være et nul af P(x).

For at bekræfte ovenstående faktum,

Lad os sige, at t er nul Q(x), hvilket betyder Q(t) = 0.

Vi ved, at r er et nul af polynomiet P(x), hvor P(x) = (x – r) Q(x),

Så vi skal tjekke om x = t også er et nul af P(x), lad os sætte x = t i P(x)

⇒ P(t) = (t – r) Q(t) = 0

Så x = t er også et nul P(x).

Derfor bevist.

Forholdet mellem nuller og koefficient

Forholdet mellem nullerne og koefficienten for den kvadratiske og kubiske ligning diskuteres nedenfor.

Forholdet mellem nuller og koefficient for andengradsligning

For en andengradsligning af formen akse²+ bx + c = 0, hvis de to nuller i andengradsligningen er α og β, så

• Sum af rod = α + β = -b/a
• Produkt af rødder = α × β = c/a

Forholdet mellem nuller og koefficient for kubikligning

Hvis α, β og γ er roden af ​​den kubiske polynomiale akse³+ bx²+ cx + d = 0, så er forholdet mellem dets nuller og koefficienter givet som følger:

• a + b + c = -b/a
• α × β × y= -d/a
• αβ + αγ + βγ = c/a

Dannelse af ligning med nuller af polynomium

• For et kvadratisk polynomium med nuller α og β, er det kvadratiske polynomium givet ved

x ² – (a + b)x + ab .

• For et kubisk polynomium med tre nuller α, β og γ, er kubisk polynomium givet ved

x ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Nuller i grafen over polynomier

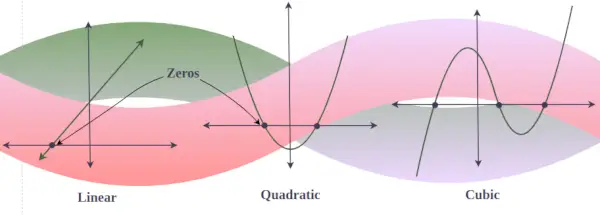
I grafen for ethvert polynomium y = f(x) er reelle nuller det punkt, hvor grafen skærer eller rører x-aksen. (da en graf med et imaginært nul aldrig skærer x-aksen). Med andre ord, hvis der er 3 reelle løsninger af et kubisk polynomium, så skærer grafen for det kubiske polynomium x-aksen tre gange, men hvis der kun er én reel løsning for et eller andet kubisk polynomium, skærer grafen kun x-aksen enkelt gang.

Grundlæggende sætning for lineær algebra

Hvis P(x) er et polynomium af grad n, vil P(x) have nøjagtig n nuller, hvoraf nogle kan gentages.

numpy linspace

Det betyder, at hvis vi lister alle nuller og lister hver enkelt k gange, når k er dens multiplicitet. Vi vil have præcis n tal på listen. Dette kan være nyttigt, da det kan give os en idé om, hvor mange nuller der skal være i et polynomium. Så vi kan stoppe med at lede efter nuller, når vi når vores nødvendige antal nuller.

En rods mangfoldighed

Antag, at vi har et polynomium P(x) = 0, som faktoriseres til,

P(x) = (x – r) ^k (x – a) ^m

Hvis r er et nul af et polynomium, og eksponenten på dets led, der producerede roden, er k, så siger vi, at r har mangfoldighed k . Nuller med en multiplicitet på 1 kaldes ofte enkel nuller og nuller med en multiplicitet på 2 kaldes dobbeltrødder af polynomiet.

Eksempel: P(x) er et grad-5 polynomium, der er blevet faktoriseret for dig. Angiv rødderne og deres mangfoldighed.

P(x) = 5x ⁵ -20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

Løsning:

Givet, P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

For at finde nuller, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Bemærk, at -1 forekommer to gange som et nul, så dens multiplicitet er 2, mens multipliciteten af ​​nul 2 er 3.

Artikler relateret til Zeros of Polynomial

• Polynomium
• Rødder af andengradsligning
• Algebraisk udtryk

Prøveproblemer på nuller af polynomium

Opgave 1: Givet at x = 2 er et nul af P(x) = x ³ +2x ² −5x−6. Find de to andre nuller.

Løsning:

Ud fra den grundlæggende sætning, vi studerede tidligere, kan vi sige, at P(x) vil have 3 nuller, fordi det er et tre graders polynomium. En af dem er x = 2.

Så vi kan omskrive P(x),

P(x) = (x – 2) Q(x)

For at finde de to andre nuller skal vi finde ud af Q(x).

Q(x) kan findes ved at dividere P(x) med (x-2).

Efter division kommer Q(x) ud at være,

Q(x) = x²+ 4x + 3

De resterende to nuller kan findes ud fra dette,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Således er de to andre nuller x = -1 og x = -3.

Opgave 2: Da x = r er et nul i et polynomium, så find ud af de andre nulpunkter i polynomiet.

P(x) = x ³ -6x ² -16x; r = −2

Løsning:

Vi ved, at x = -2 er et nul,

Så P(x) kan omskrives som, P(x) = (x + 2) Q(x) {Ved at bruge divisionsalgoritme}

For nu at finde Q(x), gør vi det samme som vi gjorde i det foregående spørgsmål, vi dividerer P(x) med (x + 2).

Vi får,

Q(x) = x²– 8x

For nu at finde de to andre nuller, faktoriser Q(x)

Q(x) = x (x – 8) = 0

Så nullerne er x = 0, 8.

Vi har således tre nuller, x = -2, 0, 8.

Opgave 3: Find nullerne i polynomiet, 4x ³ -3x ² -25x-6 = 0

Løsning:

Trick til at løse polynomialligninger med grad 3,

Find det mindste heltal, der kan gøre polynomieværdien 0, start med 1,-1,2, og så videre...

vi finder, at for x = -2 får vi værdien af ​​udtryk til at være nul.

Derfor er en af ​​rødderne -2.

I henhold til faktorsætningen, hvis a er et af nullerne i polynomiet, er (x-a) derfor faktoren for givet polynomium.

Efter dette er {x – (-2)} = (x+2) en faktor pof over polynomiet.

Vi får en andengradsligning, og et nul er der allerede.

(4x²-11x-3)(x+2) = 0

Faktoriser andengradsligningen,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Opgave 4: Find nullerne i polynomiet, 4x ⁶ – 16x ⁴ = 0

Løsning:

Polynomiet har op til grad 6, derfor eksisterer der 6 nuller af polynomiet.

4x⁴(x²-4) = 0

4x⁴(x²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Derfor er x= 0, 0, 0, 0, 2, -2

Opgave 5: Find nullerne for polynomiefunktionen f(x) = x ³ – 2x ² – 5x + 6

Løsning:

For at finde nullerne i dette polynomium sætter vi f(x) = 0 og løser for x:

f(x) = x³– 2x²– 5x + 6 = 0

Som d/a = 6

Ved rationel rodsætning er alle mulige rationelle rødder af polunomialet,

Divisorer af d/a = ±1, ±2, ±3, ±6

x = 1, i p(x), får vi

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Ved faktorsætning er x – 1 altså faktoren for p(x).

Altså x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

x³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

For nuller er p(x) = 0,

Nullpunkter for p(x) er x = 1, x = -2 og x = 3.

Øv opgaver på nuller af polynomium

1. Find alle nulpunkterne i polynomiet f(x) = x ³ – 6x ² + 11x – 6

2. Bestem alle nulpunkterne i polynomiet g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Find nullerne i polynomiet h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Bestem alle nullerne i polynomiet p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Ofte stillede spørgsmål om nuller af polynomium

Hvad er nuller i et polynomium?

Disse sådanne reelle værdier, for værdien af ​​polynomiet bliver 0, dvs. hvis p(x) er et polynomium, og p(a) = 0, så er x = a nulpunktet af p(x).

Hvordan finder man nullerne i et polynomium?

Der er forskellige metoder til forskellige polynomier til at finde nuller, såsom kvadratisk spild af mellemled og andengradsformel. Til lineær, simpel omarrangering af variable og til kubisk bruger vi en kombination af rationel rodsætning, lang division, faktorsætning og restsætning.

Kan et polynomium have mere end ét nul?

Ja, et polynomium kan have mere end et nul, faktisk kan polynomiet på n grader højst have n reelle nuller.

Hvad er multipliciteten af ​​et nul i et polynomium?

I faktoriseringsprocessen kom en faktor eller et nul af et polynomium og derefter et antal gange en faktor eller et nul, det kaldes multipliciteten af ​​denne rod.

Hvad er Algebras grundlæggende sætning?

Algebraens grundlæggende sætning siger, at Hvis P(x) er et polynomium af grad n, vil P(x) have nøjagtig n nuller, hvoraf nogle kan gentages.

Har et polynomium med en grad n altid n rigtige rødder?

Nej, et polynomium med grad n har ikke altid n reelle rødder, da nogle rødder kan være imaginære eller komplekse tal.

Hvad er graden af ​​nulpolynomium?

Graden af ​​nul polynomium er nul.

ellers java