logo

TechCodeview

Stærkt forbundne komponenter

Strongly Connected Components (SCC'er) er et grundlæggende begreb i grafteori og algoritmer. I en rettet graf, en Stærkt forbundet komponent er en delmængde af toppunkter, hvor hvert toppunkt i delmængden kan nås fra hvert andet toppunkt i samme delmængde ved at krydse de rettede kanter. At finde SCC'er af en graf kan give vigtig indsigt i grafens struktur og sammenhæng, med applikationer inden for forskellige områder som f.eks. sociale netværksanalyse, webcrawling og netværksrouting . Denne tutorial vil udforske definitionen, egenskaberne og effektive algoritmer til at identificere stærkt forbundne komponenter i grafdatastrukturer

string.compare c#

Indholdsfortegnelse



Hvad er Strongly Connected Components (SCC'er)?

EN stærkt forbundet komponent af en rettet graf er en maksimal undergraf, hvor hvert par af hjørner er gensidigt tilgængeligt. Dette betyder, at der for to knudepunkter A og B i denne undergraf er en sti fra A til B og en sti fra B til A.

For eksempel: Nedenstående graf har to stærkt forbundne komponenter {1,2,3,4} og {5,6,7}, da der er vej fra hvert hjørne til hvert andet hjørne i den samme stærkt forbundne komponent.

scc_fianldrawio

Stærkt forbundet komponent



Hvorfor er SCC'er (Strongly Connected Components) vigtige?

At forstå SCC'er er afgørende for forskellige applikationer såsom:

  • Netværksanalyse : Identifikation af klynger af tæt forbundne noder.
  • Optimering af webcrawlere : Bestemmelse af dele af webgrafen, der er tæt forbundet.
  • Afhængighedsopløsning : I software forstå hvilke moduler der er indbyrdes afhængige.

Forskellen mellem forbundne og stærkt forbundne komponenter ( SCC'er)

Forbindelse i en urettet graf refererer til, om to hjørner kan nås fra hinanden eller ej. To hjørner siges at være forbundet, hvis der er sti mellem dem. I mellemtiden Stærkt forbundet gælder kun for rettede grafer . En undergraf af en rettet graf anses for at være en Stærkt forbundne komponenter (SCC) hvis og kun hvis for hvert par af hjørner EN og B , der findes en vej fra EN til B og en vej fra B til EN . Lad os se hvorfor standard dfs metode til at finde forbundne komponenter i en graf kan ikke bruges til at bestemme stærkt forbundne komponenter.

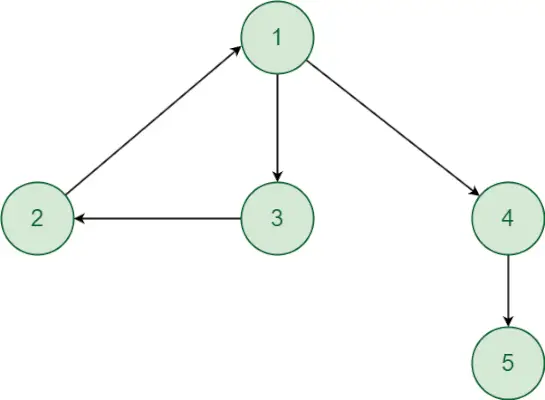
Overvej følgende graf:



scc_fianldrawio

Lad os nu starte a dfs opkald fra toppunkt 1 for at besøge andre toppunkter.

dfs_finaldrawio

Hvorfor kan konventionel DFS-metode ikke bruges til at finde de stærkt forbundne komponenter?

Alle toppunkter kan nås fra toppunkt 1. Men toppunkter 1 og 5,6,7 kan ikke være i den samme stærkt forbundne komponent, fordi der ikke er nogen rettet vej fra toppunkt 5,6 eller 7 til toppunkt 1. Grafen har to stærkt forbundne punkter. tilsluttede komponenter {1,2,3,4} og {5,6,7}. Så den konventionelle dfs-metode kan ikke bruges til at finde de stærkt forbundne komponenter.

vælg som

Tilslutning af to stærkt forbundne komponenter med en ensrettet kant

To forskellige forbundne komponenter bliver til en enkelt komponent, hvis en kant tilføjes mellem et toppunkt fra en komponent til et toppunkt af en anden komponent. Men dette er ikke tilfældet i stærkt forbundne komponenter. To stærkt forbundne komponenter bliver ikke til en enkelt stærkt forbundet komponent, hvis der kun er en ensrettet kant fra en SCC til en anden SCC.

hvad xd betyder

unidrawio-(2)

Brute Force-tilgang til at finde stærkt forbundne komponenter

Den enkle metode vil være, at for hvert toppunkt i (som ikke er en del af nogen stærkt komponent) skal du finde de hjørner, som vil være den del af stærkt forbundet komponent, der indeholder toppunkt i. To toppunkter i og j vil være i den samme stærkt forbundne komponent, hvis der er en rettet vej fra toppunkt i til toppunkt j og omvendt.

Lad os forstå tilgangen ved hjælp af følgende eksempel:

eksempel tegne

  • Starter med toppunkt 1. Der er vej fra toppunkt 1 til toppunkt 2 og omvendt. På samme måde er der en vej fra toppunkt 1 til toppunkt 3 og omvendt. Så toppunkt 2 og 3 vil være i den samme stærkt forbundne komponent som toppunkt 1. Selvom der er rettet vej fra toppunkt 1 til toppunkt 4 og toppunkt 5. Men der er ingen rettet vej fra toppunkt 4,5 til toppunkt 1, så toppunkt 4 og 5 vil ikke være i den samme Strongly Connected Component som vertex 1. Derfor danner Vertex 1,2 og 3 en Strongly Connected Component.
  • For Vertex 2 og 3 er der allerede fastlagt en stærkt forbundet komponent.
  • For toppunkt 4 er der en sti fra toppunkt 4 til toppunkt 5, men der er ingen vej fra toppunkt 5 til toppunkt 4. Så toppunkt 4 og 5 vil ikke være i den samme stærkt forbundne komponent. Så både Vertex 4 og Vertex 5 vil være en del af Single Strongly Connected Component.
  • Derfor vil der være 3 stærkt forbundne komponent {1,2,3}, {4} og {5}.

Nedenfor er implementeringen af ​​ovenstående tilgang:

C++ 
#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vektor & vis) { // Hvis curr node er destination return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } returner falsk;  } // For at fortælle om der er sti fra kilde til // destination bool isPath(int src, int des, vektor>& adj) { vektor vis(adj.størrelse() + 1, 0);  return dfs(src, des, adj, vis);  } // Funktion til at returnere alle de stærkt forbundne //-komponenter i en graf.  vektor> findSCC(int n, vektor>& a) { // Gemmer alle de stærkt forbundne komponenter.  vektor> ans;  // Gemmer, om et vertex er en del af en hvilken som helst Stærkt // Connected Component-vektor er_scc(n + 1, 0);  vektor> adj(n + 1);  for (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> kanter{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vektor> ans = obj.findSCC(V, kanter);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>
Java 
import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, Liste vis) { // Hvis curr node er destination return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } returner falsk;  } // For at fortælle om der er sti fra kilde til // destination boolean isPath(int src, int des, Liste> adj) { Liste vis = new ArrayList(adj.size() + 1);  for (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> findSCC(int n, Liste> a) { // Gemmer alle de stærkt forbundne komponenter.  Liste> ans = new ArrayList();  // Gemmer, om et toppunkt er en del af en hvilken som helst Strongly // Connected Component List is_scc = ny ArrayList(n + 1);  for (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = ny ArrayList();  for (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List edge : a) { adj.get(edge.get(0)).add(edge.get(1));  } // At krydse alle hjørnerne for (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = new ArrayList();  scc.add(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> edges = new ArrayList();  edges.add(ny ArrayList(List.of(1, 3)));  edges.add(ny ArrayList(List.of(1, 4)));  edges.add(ny ArrayList(List.of(2, 1)));  edges.add(ny ArrayList(List.of(3, 2)));  edges.add(ny ArrayList(List.of(4, 5)));  Liste> ans = obj.findSCC(V, kanter);  System.out.println('Stærkt forbundne komponenter er:');  for (liste x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Denne kode er bidraget af shivamgupta310570>
Python 
class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570>
C# 
using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, Liste vis) { // Hvis curr node er destinationen, return true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x i adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } returner falsk;  } // At fortælle om der er en sti fra kilde til destination public bool IsPath(int src, int des, Liste> adj) { var show = ny liste (adj.Tæl + 1);  for (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> FindSCC(int n, Liste> a) { // Gemmer alle de stærkt forbundne komponenter var ans = new List>();  // Gemmer, om et toppunkt er en del af en stærkt forbundet komponent var isScc = new List (n + 1);  for (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  for (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } for (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  for (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> kanter = ny liste> { ny liste { 1, 3 }, ny liste { 1, 4 }, ny liste { 2, 1 }, ny liste { 3, 2 }, ny liste { 4, 5 } };  Liste> ans = obj.FindSCC(V, kanter);  Console.WriteLine('Stærkt forbundne komponenter er:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Denne kode er bidraget af shivamgupta310570>
Javascript 
class GFG {  // Function to reach the destination using DFS  dfs(curr, des, adj, vis) {  // If the current node is the destination, return true  if (curr === des) {  return true;  }  vis[curr] = 1;  for (let x of adj[curr]) {  if (!vis[x]) {  if (this.dfs(x, des, adj, vis)) {  return true;  }  }  }  return false;  }  // Check whether there is a path from source to destination  isPath(src, des, adj) {  const vis = new Array(adj.length + 1).fill(0);  return this.dfs(src, des, adj, vis);  }  // Function to find all strongly connected components of a graph  findSCC(n, a) {  // Stores all strongly connected components  const ans = [];  // Stores whether a vertex is part of any Strongly Connected Component  const is_scc = new Array(n + 1).fill(0);  const adj = new Array(n + 1).fill().map(() =>[]);  for (lad i = 0; i< a.length; i++) {  adj[a[i][0]].push(a[i][1]);  }  // Traversing all the vertices  for (let i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not part of any SCC,  // insert it into a new SCC list and check  // for other vertices that can be part of this list.  const scc = [i];  for (let j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push(j);  }  }  // Insert the SCC containing vertex i into the final list.  ans.push(scc);  }  }  return ans;  } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [  [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) {  console.log(x.join(' ')); } // This code is contributed by shivamgupta310570>
Produktion 
Strongly Connected Components are: 1 2 3 4 5>

Tidskompleksitet: O(n * (n + m)), fordi vi for hvert par af hjørner kontrollerer, om der findes en sti mellem dem.
Hjælpeplads: O(N)

overskrift i illustrator

Effektiv tilgang til at finde stærkt forbundne komponenter (SCC'er)

For at finde SCC'er i en graf kan vi bruge algoritmer som f.eks Kosarajus algoritme eller Tarjans algoritme . Lad os udforske disse algoritmer trin for trin.

1. Kosarajus algoritme :

Kosarajus algoritme involverer to hovedfaser:

  1. Udførelse af dybde-først-søgning (DFS) på den originale graf :
    • Vi laver først en DFS på den originale graf og registrerer sluttider for noder (dvs. det tidspunkt, hvor DFS er færdig med at udforske en node fuldstændigt).
  2. Udførelse af DFS på den transponerede graf :
    • Vi vender derefter retningen af ​​alle kanter i grafen for at skabe den transponerede graf.
    • Dernæst udfører vi en DFS på den transponerede graf, idet vi betragter noder i faldende rækkefølge efter deres sluttider registreret i den første fase.
    • Hver DFS-gennemgang i denne fase vil give os et SCC.

Her er en forenklet version af Kosarajus algoritme:

  1. DFS på original graf : Optag sluttider.
  2. Transponer grafen : Vend alle kanter.
  3. DFS på transponeret graf : Behandle noder i rækkefølge efter faldende sluttider for at finde SCC'er.

2. Tarjans algoritme :

Tarjans algoritme er mere effektiv, fordi den finder SCC'er i et enkelt DFS-pas ved hjælp af en stak og noget ekstra bogføring:

  1. DFS Traversal : Vedligehold under DFS et indeks for hver knude og det mindste indeks (lav-link værdi), der kan nås fra knudepunktet.
  2. Stak : Hold styr på noder i øjeblikket i rekursionsstakken (en del af den aktuelle SCC, der udforskes).
  3. Identifikation af SCC'er : Når en nodes lav-link værdi er lig med dens indeks, betyder det, at vi har fundet en SCC. Pop alle noder fra stakken, indtil vi når den aktuelle node.

Her er en forenklet oversigt over Tarjans algoritme:

  1. Initialiserindex>til 0.
  2. Udfør DFS for hver ubesøgt node.
    • Indstil nodens indeks og lav-link værdi.
    • Skub noden ind på stakken.
    • For hver tilstødende node skal du enten udføre DFS, hvis den ikke er besøgt, eller opdatere lavlinkværdien, hvis den er i stakken.
    • Hvis nodens lav-link værdi er lig med dens indeks, pop noder fra stakken for at danne en SCC.

Konklusion

Forståelse og finde stærkt forbundne komponenter i en rettet graf er afgørende for mange applikationer inden for datalogi. Kosaraju's og Tarjans Algoritmer er effektive måder at identificere SCC'er på, hver med deres egen tilgang og fordele. Ved at mestre disse begreber kan du bedre analysere og optimere strukturen og adfærden i komplekse netværk.