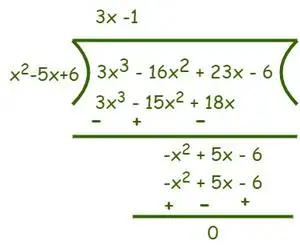Kubisk ligning er en matematisk ligning, hvor et polynomium på grad 3 er lig med en konstant eller et andet polynomium på maksimal grad 2. Standardrepræsentationen af ​​den kubiske ligning er økse ³ +bx ² +cx+d = 0 hvor a, b, c og d er reelle tal. Nogle eksempler på kubiske ligninger er x ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 etc.

Indholdsfortegnelse

• Polynomisk definition
• Ligningsgrad
• Definition af kubisk ligning
• Hvordan løses kubiske ligninger?
• Løsning af kubiske ligninger
• Løsning af kubikligning ved hjælp af faktorer
• Løsning af kubikligning ved hjælp af grafisk metode
• Problemer baseret på løsning af kubikligninger
• Øv opgaver om løsning af kubiske ligninger

For at lære, hvordan man løser kubiske ligninger, skal vi først lære om polynomier, graden af ​​polynomiet og andre. I denne artikel vil vi lære om, polynomier, polynomiale ligninger, løsning af kubiske ligninger eller hvordan man løser kubiske ligninger og andre i detaljer.

Polynomisk definition

Polynomium er defineret som følger,

EN polynomium er et algebraisk udtryk, hvor styrken af ​​en variabel er et ikke-negativt heltal. Den generelle form for et polynomium er a₀xⁿ+ a₁x^n-1+ a₂x^n-2+… + a_n. Afhængigt af den maksimale effekt af variablen kan et polynomium klassificeres som et monomial, binomial, trinomial og så videre.

Hvad er en ligning?

En ligning er defineret som følger,

En ligning er et polynomium, der er lig med en numerisk værdi eller et hvilket som helst andet polynomium. For eksempel er x + 2 et polynomium, men x + 2 = 5 er en ligning. På samme måde er 2x + 3 = x + 1 også en ligning, hvorimod 2x + 3 og x + 1 er polynomier individuelt.

Ligningsgrad

Definitionen af ​​ligningsgraden er angivet nedenfor:

Grad af en ligning er defineret som den maksimale effekt, som variablen besidder i en ligning.

Baseret på graden af ​​ligningen kan en ligning klassificeres som følger:

• Lineær ligning
• Kvadratisk ligning
• Kubisk ligning
• Biquadratisk ligning

Lineær ligning

Ligningen, hvor den maksimale effekt af variablen er 1, kaldes en lineær ligning.

• For eksempel 3x +1 = 0

Kvadratisk polynomium

Ligningen, hvor den maksimale effekt af variablen er 2, er en andengradsligning.

• For eksempel 3x²+x+1 = 0

Kubisk ligning

Ligningen, hvor den maksimale effekt af variablen er 3, kaldes en kubikligning.

• For eksempel 5x³+3x²+x+1 = 0

Biquadratisk polynomium

Ligningen, hvor den maksimale potens af variablen er 4, kaldes et biquadratisk polynomium eller kvartpolynomium.

• For eksempel 5x⁴+4x³+3x²+2x+1 = 0

Definition af kubisk ligning

Kubisk ligning er en algebraisk ligning, hvor den højeste grad af polynomiet er 3. Nogle eksempler på kubiske ligninger er 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 osv.

Den generelle form for en kubisk ligning er,

økse ³ + bx ² + cx + d = 0, a ≠ 0

Hvor,

• a, b, og c er koefficienterne for variable og deres eksponenater og d er konstanten, og
• a, b, c og d er reelle tal.

Hvordan løses kubiske ligninger?

En kubikligning er en ligning med grad tre. Det har tre løsninger, og det kan nemt løses ved at følge trinene tilføjet nedenfor,

Trin 1: Find en løsning på den kubiske ligning ved at trykke og prøve metode. Antag, at vi har en kubisk ligning P(x), så find for enhver x = a, P(a) = 0 ved at tage, x = 0, ±1, ±2, ±3, … og så.

Trin 2: Når vi får, P(a) = 0, find faktoren (x – a) af P(x)

Trin 3: Divider P(x) med (x – a) for at få en andengradsligning, sig Q(x) ved hjælp af polynomial division.

Trin 4: Faktariser andengradsligningen Q(x) for at få faktorerne som (x – b) og (x – c).

Trin 5: (x – a), (x – b) og (x – c) er faktorerne for P(x), og ved at løse hver faktor får vi rødderne til ligningen som, a, b og c.

Lær mere om, Delingspolynomium

Løsning af kubiske ligninger

EN Kubisk ligning kan løses på to måder

• Ved at reducere det til en andengradsligning og derefter løse det enten ved faktorisering eller andengradsformlen
• Ved grafisk metode

EN Kubisk ligning har tre rødder. Disse rødder kan være ægte eller imaginære. Der kan også være forskellige rødder eller to ens og en forskellig rod og alle tre samme rødder.

Det skal bemærkes, at for enhver ligning, herunder Kubiske ligninger , skal ligningen altid arrangeres i sin standardform først, før ligningen løses.

For eksempel, hvis den givne ligning er 2x²-5 = x + 4/x, så skal vi omarrangere dette til dets standardform, dvs. 2x³-x²-5x-4 = 0. Nu kan vi løse ligningen ved hjælp af en hvilken som helst passende metode.

Løsning af kubikligning ved hjælp af faktorer

Løsningen af ​​kubisk ligning ved hjælp af faktorsætning er forklaret ved hjælp af eksemplet tilføjet nedenfor,

streng sammenligne c#

Eksempel: Find rødderne af ligning f(x) = 3x ³ -16x ² + 23x − 6 = 0.

Løsning:

Givet udtryk: f(x) = 3x³-16x²+ 23x − 6 = 0

Først faktoriser polynomiet for at få rødder

Da konstanten er -6, er de mulige faktorer 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

java erstatte alle

f(6) = 648 – 576 + 138 – 6 ≠ 0

Det ved vi iflg Faktorsætning hvis f(a) = 0, så er (x-a) en faktor af f(x)

Så (x – 2) og (x – 3) er faktorer af f(x). Derfor vil produktet af (x – 2) og (x – 3) også være faktor af f(x). For nu at finde de resterende faktorer, brug den lange divisionsmetode og divider f(x) med produktet af (x – 2) og (x – 3)

Derfor er Divisor = (x – 2)(x – 3) = (x²– 5x + 6) og udbytte = 3x³-16x²+ 23x − 6. Divider nu som vist nedenfor,

Efter division får vi (3x- 1) som kvotient og rest er 0. Nu som pr Divisionsalgoritme vi ved det Udbytte = Divisor×Quotient+Rest.

⇒ f(x) = (3x³-16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Da f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 eller 3x-1 = 0

Nu tager vi 3x-1 = 0 ⇒ x = 1/3, da vi allerede kender to rødder fra x²– 5x + 6, som er 2 og 3

Så,

Rødder af det givne Kubisk ligning er 1/3, 2 og 3.

Løsning af kubikligning ved hjælp af grafisk metode

En kubikligning løses grafisk, når man ikke kan løse den givne ligning ved hjælp af andre teknikker. Så vi har brug for en nøjagtig tegning af den givne kubiske ligning. Ligningens rødder er punktet/punkterne, hvor grafen krydser X-aksen, hvis ligningen er i vilkårene af x, og hvis ligningen er i vilkårene af y, så er ligningens rødder de punkter, hvor grafen skærer Y-aksen.

Antallet af reelle løsninger til kubikligningen er lig med antallet af gange kubikligningens graf krydser X-aksen.

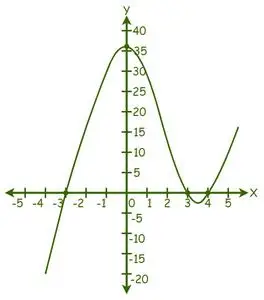
Eksempel: Find rødderne af ligningen f(x) = x ³ - 4x ² − 9x + 36 = 0, ved hjælp af den grafiske metode.

Løsning:

Givet udtryk: f(x) = x³- 4x²− 9x + 36 = 0.

Nu skal du blot erstatte tilfældige værdier for x i grafen for den givne funktion:

x	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

Vi kan se, at grafen har skåret X-aksen i 3 punkter, derfor er der 3 rigtige løsninger.

Fra grafen er løsningerne: x = -3, x = 3 og x = 4.

Derfor er rødderne til den givne ligning -3, 3 og 4.

Læs mere,

• Lineær ligning
• Løsning af andengradsligning
• Faktorerende polynomier

Problemer baseret på løsning af kubikligninger

Opgave 1: Find rødderne af f(x) = x ³ – 4x ² -3x + 6 = 0.

Løsning:

Givet udtryk: f(x) = x³– 4x²-3x + 6 = 0.

Først faktoriser polynomiet for at få rødder.

Da konstanten er +6, er de mulige faktorer 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Altså ifølge Faktorsætning (x – 1) er en faktor i den givne ligning. For nu at finde de resterende faktorer, brug den lange divisionsmetode.

Ifølge Divisionsalgoritme vi kan skrive,

Så f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 eller (x²– 3x – 6) = 0

Vi ved, at rødderne af en andengradsligning øks²+ bx + c = 0 er,

rækkefølge tilfældigt i sql

x = [-b ± √(b²-4ac)]/2a

Derfor, for (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Derfor er rødderne af den givne kubiske ligning 1, (3+√33)/2 og (3–√33)/2.

Opgave 2: Find rødderne til ligning f(x) = 4x ³ – 10x ² + 4x = 0.

Løsning:

Givet udtryk: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 eller 4x – 2 = 0, x – 2 = 0

⇒ x = 0 eller x = 1/2 eller x = 2

Derfor er rødderne til den givne ligning 0, 1/2 og 2.

Opgave 3: Find rødderne til ligning f(x) = x ³ + 3x ² + x + 3 = 0.

Løsning:

Givet udtryk: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 eller x²+1 = 0

⇒ x = -3, ±i

Så den givne ligning har en reel rod, dvs. -3, og to imaginære rødder, dvs. ±i.

Opgave 4: Find rødderne til ligning f(x) = x ³ – 7x ² – x + 7 = 0.

Løsning:

Givet udtryk,

f(x) = x³– 3x²– 5x + 7 = 0

Faktoriser først ligningen, f(x): x³– 3x²– 5x + 7= 0

Det kan indregnes i (x-7)(x+1)(x-1) = 0

Efter at have faktoriseret polynomiet kan vi finde rødderne ved at sidestille hver faktor med nul. For eksempel:

reference datatyper i java

• x – 7 = 0, så x = 7
• x + 1 = 0, så x = -1
• x – 1 = 0, så x = 1

Så rødderne af ligningen f(x): x³– 3x²– 5x + 7 = 0 er

• x = 7
• x = -1
• x = 1

Opgave 5: Find rødderne til ligning f(x) = x ³ - 6x ² + 11x − 6 = 0, ved brug af den grafiske metode.

Løsning:

Givet udtryk: f(x) = x³- 6x²+ 11x − 6 = 0.

Nu skal du blot erstatte tilfældige værdier for x i grafen for den givne funktion:

x	1	2	3	4	5
f(x)	0	0	0	6	24

Vi kan se, at grafen har skåret X-aksen i 3 punkter, derfor er der 3 rigtige løsninger.

Fra grafen er løsningerne: x = 1, x = 2 og x = 3.

Derfor er rødderne til den givne ligning 1, 2 og 3.

Øv opgaver om løsning af kubiske ligninger

Forskellige praksisproblemer relateret til kubiske ligninger er tilføjet nedenfor. Løs disse problemer for fuldt ud at forstå konceptet Hvordan løses kubisk ligning?

P1. Løs den kubiske ligning, 3x³+ 2x²– 11x + 7 = 0.

1 af 1000,00

P2. Find rødderne til kubisk ligning, 4x³– 12x²+ 17 = 0.

P3. Løs den kubiske ligning, x³+ 4x²– x + 3 = 0 ved hjælp af grafisk metode.

P4. Find det tal, der opfylder, -9x³+ 11x²– 8x + 2 = 0.

Ofte stillede spørgsmål om løsning af kubiske ligninger

1. Hvad er kubikligninger?

Kubiske ligninger er de algebraiske ligninger, hvor den maksimale potens af en variabel er 3

2. Hvordan faktoriserer du en kubikligning?

Vi kan faktorisere en kubisk ligning på to måder. Først ved at tage et lineært udtryk fælles fra den givne kubiske ligning, så vil vi have et lineært og et kvadratisk udtryk som et produkt. Denne andengradsligning kan faktoriseres yderligere for at få alle faktorerne. Den anden metode er at finde et nul af den givne kubiske ligning ved at sætte tilfældige værdier. Den værdi, for hvilken vi får ligningens værdi til at være nul, vil være en af ​​nullerne i den givne kubiske ligning. Brug nu faktorsætningen til at danne et lineært udtryk, lad os sige x-a og dividere den givne kubiske ligning med dette udtryk, som vil give en andengradsligning som kvotient. Denne opnåede andengradsligning kan faktoriseres yderligere for at få alle faktorerne.

3. Hvordan løser man en kubikligning grafisk?

For at løse en kubikligning grafisk indsætte tilfældige værdier for x i den givne kubikligning og løse, får du værdierne af y. Plot disse opnåede værdier på grafen. Find de koordinater, hvor grafen skærer x-aksen. Disse koordinater er løsningen af ​​den kubiske ligning.

4. Kan alle kubikligninger løses nøjagtigt?

Enhver ligning, der har ulige magt, skal have én reel rod. Derfor skal en kubisk ligning have mindst én reel rod, i modsætning til en andengradsligning, hvor begge rødder kan være imaginære, når diskriminanten er mindre end nul.

5. Kan en kubikligning have flere løsninger?

Ja, kubikligninger kan have flere løsninger, da en kubikligning kan have op til tre forskellige reelle rødder.

6. Hvad mener du med en ligningsgrad?

Den maksimale effekt, som variablen besidder i en ligning, kaldes graden af ​​et polynomium.

7. Hvad er forskellen mellem et polynomium og en ligning?

Polynomium er simpelthen en algebraisk ligning, hvor styrken af ​​variablen er et ikke-negativt heltal. Når dette polynomium sidestilles (=) med en numerisk værdi eller et andet polynomium, kaldes det en ligning.

8. Hvad er faktorsætningen for kubiske ligninger?

Faktorsætning siger, at hvis r er en rod (løsning) af den kubiske ligningsakse³+ bx²+ cx + d = 0, så er x – r en faktor i ligningen.

9. Hvad hvis jeg ikke kan finde præcise løsninger ved hjælp af formler?

Hvis det virker umuligt at finde nøjagtige løsninger, kan vi bruge de numeriske metoder som iterative metoder (f.eks. Newtons metode) til at tilnærme ligningens rødder.

Lær mere om Newton Raphsons metode .